doi: 10.56294/dm2023170

ORIGINAL

Gray Level Homogeneity Analysis: A Novel Approach

Análisis de Homogeneidad de Niveles de Gris: Un Nuevo Enfoque

Abdelhamid El Beghdadi¹ *, Mohammed Merzougui¹ *, Ahmad El Allaoui² *

¹Mohammed I University. Oujda, Morocco.

²FST Errachidia, Moulay Ismail University. Meknes, Morocco.

Cite as: El Beghdadi A, Merzougui M, El Allaoui A. Gray Level Homogeneity Analysis: A Novel Approach. Data and Metadata. 2023;2:170. https://doi.org/10.56294/dm2023170

Submitted: 10-09-2023                           Revised: 02-11-2023                            Accepted: 29-12-2023                       Published: 30-12-2023

Editor: Prof. Dr. Javier González Argote

Guest Editor: Yousef Farhaoui

Note: paper presented at the International Conference on Artificial Intelligence and Smart Environments (ICAISE’2023).

ABSTRACT

In this article, we propose a method that helps us to analyze the homogeneity of gray levels locally by calculating a coefficient for each pixel based on the nature of neighboring pixels. This principle of encoding pixels according to their adjacent neighbors is described the nature of the distribution of gray levels within the image and measures their degree of homogeneity locally. This allows us to detect the different regions of the image and their contours based on the coefficient of homogeneity of the gray levels. In addition, this allows us to exploit these homogeneity coefficients to restructure regions of the image, extract and enhance the image contours while reducing the noise present in the image. This homogeneity study principle has several functions in the study and analysis of image texture, as do other methods of homogeneity assessment, such as the local contrast descriptor (LCD) and the co-occurrence matrix.

Keywords: CLH Matrix; Co-occurrence Matrix; Sobel; LCD; Denoising; Texture; Segmentation; Histogram.

RESUMEN

En este artículo, proponemos un método que nos ayuda a analizar la homogeneidad de los niveles de gris localmente calculando un coeficiente para cada píxel en función de la naturaleza de los píxeles vecinos. Este principio de codificación de los píxeles en función de sus vecinos adyacentes permite describir la naturaleza de la distribución de los niveles de gris dentro de la imagen y medir su grado de homogeneidad localmente. Esto nos permite detectar las distintas regiones de la imagen y sus contornos basándonos en el coeficiente de homogeneidad de los niveles de gris. Además, esto nos permite explotar estos coeficientes de homogeneidad para reestructurar regiones de la imagen, extraer y realzar los contornos de la imagen reduciendo al mismo tiempo el ruido presente en la imagen. Este principio de estudio de la homogeneidad tiene varias funciones en el estudio y análisis de la textura de las imágenes, al igual que otros métodos de evaluación de la homogeneidad, como el descriptor de contraste local (LCD) y la matriz de co-ocurrencia.

Palabras clave: Matriz CLH; Matriz de Co-ocurrencia; Sobel; LCD; Denoising; Textura; Segmentación; Histograma.

INTRODUCCIÓN

The study of the spatial structure of gray levels using various techniques to determine the descriptor of visual patterns is known as texture analysis, and it is a significant field in the literature on image processing. In order to enhance texture analysis, this field has a number of noteworthy strengths. Local geometric primitives, random field modeling, and fractals are some of the techniques used; others are based on the analysis and characterization of pixel distribution, the measurement of gray level homogeneity, or statistical evaluation of texture. Among the methods of analysis in this context, we find:

The co-occurrence matrix of gray levels (GLCM), often referred to as the Haralick method,⁽¹⁾ is a texture analysis approach that calculates the likelihood that two grayscale level pairings would coincide in an image. The statistical characteristics of this matrix can be used to assess the homogeneity of textures and pixels in a picture. There are many GLCM qualities that may be used to evaluate a texture's homogeneity.

The local contrast distribution is assessed using the LCD (local contrast distribution) approach.² It is important for examining the homogeneity of pixels and textures since it lets you measure the variation of gray or color levels in various sections of the image. This method may be applied in many domains where texture analysis is essential, including computer vision, object identification, medical image processing, and other areas.

In this work, we propose a method for analyzing texture based on pixel encoding to characterize image texture by comparing the gray level of the central pixel with its eight neighbors. This principle focuses on studying the homogeneity of gray levels between different regions, allowing us to determine the pixel density at the same gray level.⁽³⁾ This encoding method specifically focuses on the homogeneity of gray levels, which is more crucial than the LCD and Haralick methods. This is because each image has unique encoding coefficient, while the Haralick method's parameters are associated with distance and direction. In addition, our calculation method is simpler and less time-consuming than LCD and GLCM. These encoding coefficients will be used to detect image areas, improve weak contours, and reduce noise. This method can be applied in various areas, as we will discuss in this work.

Matrice CLH

The coding principle of the central pixel is the cardinal of the central pixel and its neighbors of the same gray level.

Figure 1.  Coding of the pixel as a function of its adjacent neighbors

The coding matrix that we will define for any image is as follows:

A is the generated matrix, which can be called the matrix of coefficients of local homogeneity, as noted by CLH.

By definition, the coding matrix coefficients range from 1 to 9, with each coefficient corresponding to a model depicted in figure 1. The central pixel, possessing the highest coefficient, exhibits the greatest uniformity with its neighboring pixels. A coefficient of 9 signifies that the pixel matches the color of its neighbors, while coefficients 8 and 7 indicate a homogeneity level almost equivalent to coefficient 9. These three coefficients (9, 8, and 7) signify a notable uniformity in local gray levels. However, the 3x3 matrix surrounding central coefficients 1, 2, and 3 demonstrates lower homogeneity with its neighbors, representing a mixture of gray levels or noise. Particularly, coefficient 1 suggests a foreign pixel among its eight neighboring pixels.^(4,5)

Regarding coefficients 4, 5, and 6, frequently located at region borders, with emphasis on index 6 being the most likely, these coefficients portray a 3x3 matrix as a region characterized by average homogeneity.

Representation of the matrix CLH

We can describe and distinguish image regions according to their homogeneity levels by applying the coefficients that are obtained from the CLH matrix. To effectively represent the matrix as an image, we propose to augment the coding coefficients in this framework.

Let A be the CLH matrix with: A (i,j) ∈ {1,...,9}

The 255/8 scaling factor is utilized to increase the distance between homogeneity coefficients in order to visually highlight the smoothing change as a function of gray levels.

Figure 2. (a): original image, (b): image written by the CLH matrix associated with the original image, (c): image written by the CLH matrix associated with the image (b)

The matrix serves as an efficient method for identifying boundaries within image shapes characterized by higher levels of gray level homogeneity. However, challenges arise when dealing with shapes exhibiting lower homogeneity. The resolution to this issue lies in the second-degree matrix, exemplified in image (c), which effectively delineates the boundaries of regions with lower homogeneity.⁽⁶⁾

Histogram of the matrix CLH

The quantitative distribution of coding coefficients, or the histogram of the CLH matrix, can help us understand the image's characteristics and more clearly illustrate how homogeneous a given pixel is with its neighbors.

Figure 3. The histogram of the CLH matrix associated with the image

The coding coefficients, which show how homogeneous a pixel is with its neighbors, are displayed in the histogram. The coefficients that characterize the image's texture are presumably the most quantitative. This histogram analysis leads us to the conclusion that frequency coefficients of homogeneity can be used to categorize the nature of images.⁽⁷⁾ At this point, we can define an indicator that, in general, captures the essence of the picture and use it to get a sense of the most common and likely homogeneity coefficients. The following is the indicator.^(8,10)

h is the average rate of the coefficients of the CLH matrix, which means the homogeneity rate of pixels among themselves.

Figure 4. The histogram (first) reflects an average homogeneity with h=8, indicating that the corresponding image is more uniform. On the other hand, histogram (second) signifies an average homogeneity with h=1, suggesting that the image associated with this histogram exhibits lower homogeneity

Detection of regions

Our endeavor involves employing the coefficients from the CLH matrix to identify image regions. By relying on these indicators, we can ascertain the texture of the image and delineate its component shapes based on homogeneity.^{(11,12,13,14)}

In this phase, we suggest a computation relying on the coding coefficients to bring grayscale levels into closer alignment with their neighbors and standardize their distribution. This algorithm is systematically applied in a recursive manner to a submatrix of dimensions 2x2.

In line with this principle, the suggested approach for delineating image regions through the coefficients of the CLH matrix in the new image is elucidated by the following formula:

The formula for analyzing gray levels aids in precisely delineating the borders of regions characterized by similar gray level homogeneity. This enables the identification of distinct areas within the image, categorizing them as either having weak or strong homogeneity, and facilitating the differentiation of nearly identical regions.^(15,17)

Figure 5. (a): initial image, (b): new image created by the initial image with its CLH matrix according to the mathematical formula (1)

Improve weak contours

Various techniques such as Sobel, Roberts, and Prewitt^(1,14,17) are commonly employed to identify image contours, presenting them in a straightforward and comprehensible manner. Several approaches exist to enhance the accuracy of detecting image contours.⁽¹¹⁾ The challenge at hand involves refining faint or imperceptible contours within the image, a prevalent issue in image processing, particularly in fields like radiography (in medicine), where meticulous analysis of image contours is crucial. The CLH matrix proves advantageous in addressing this concern by offering improvements to weak contours. The fundamental approach involves applying a specific edge detection operator to the image processed through the coding matrix, as outlined in the preceding mathematical formula.⁽¹⁾ Below, we present comparisons of edge detection using the same operator (Sobel) on the original image and the image processed by CLH.

Figure 6. (a): the original image, (b): contours of the image by Sobel, (c): contours of the image by Sobel processed by CLH

The contours of the image processed by CLH are sharper and more distinct than the other thanks to the same Sobel mask; the masks that were used are:

The operator uses convolution matrices. The matrix of size 3x3 will convoled with the image to calculate approximations of the horizontal and vertical derivatives. Let M be the initial image or the image processed by CHL matrix.

At each point, the horizontal and vertical gradient approximations can be combined as follows to obtain an approximation of the gradient norm:

Noise reduction

Image noise poses a significant challenge in the realm of image processing, prompting ongoing efforts to enhance image quality and recover lost information.^(18,19) Consequently, researchers have dedicated considerable work to devising methods and techniques for noise removal from images,^(7,10,18,20) striving to minimize noise and restore images closer to their original state.

At this juncture, we aim to employ our approach, which computes the average of gray levels based on the coefficients of the CLH matrix. Leveraging these coefficients allows us to identify pixels associated with the smallest coefficients, which can be deemed as noisy pixels. This distinction is crucial for determining the pixels to be addressed, contingent on the chosen homogeneity level for our computation. We retain the gray levels for pixels that exhibit greater homogeneity with their neighbors. The calculation formula is expressed as follows:

with: (n,m)∈{-1,0,1}²  and  i+n>0  ,j+m>0

I the noisy image, A is the CLH matrix associated to the figure 1.

c∈ {1, ..., 9} is the coefficient corresponding to the degree of homogeneity chosen for the pixels we will process.

Figure 7. Example of noise reduction with the choice c=5

RESULTS AND DISCUSSION

In this study, the homogeneity matrix of gray levels was used to detect and improve contours in texture analysis applications, as well as to improve contrast between image regions and reduce noise.

With regard to the image contour detection by the gray level homogeneity matrix, it is highly sensitive to variations in gray levels between the regions of the image and detects the contours for all variations, which can result in noise due to the large number of contours in the images, especially those that are non-homogeneous and have irregular areas. However, the importance of the homogeneity matrix lies in the detection of contours between regions with almost equal levels of gray and which cannot be distinguished by the naked eye, which is an important feature of the matrix of homogeneity compared to other methods of contour detection, as we will see through various examples on this subject.⁽²¹⁾

Figure 8. Here are some examples of detection of the contours of some images by the CLH matrix and their comparison with the Canny method

Note, for example, that the LCH matrix gives all the details about changing gray levels, which explains the large number of edges in some examples, unlike other methods that specify edges for areas concerned only in the image. The importance of the matrix lies in tracking all changes in the homogeneity of gray levels in the image.

Figure 9. Example of detection of contours between areas with almost equal levels of gray

For edge detection in images with nearly equal gray levels, it poses a significant challenge for conventional methods (Canny, Sobel, …). However, with the LCH matrix approach, contours between image regions can be identified, regardless of their differences, whether distinguishable by the naked eye or not.

With regard to improving the contours of an image using the CLH matrix, it is very excellent, thanks to which we can clearly show the weak contours in an image, as well as show the relatively invisible contours. This is a very important thing for medical imaging and in other areas.

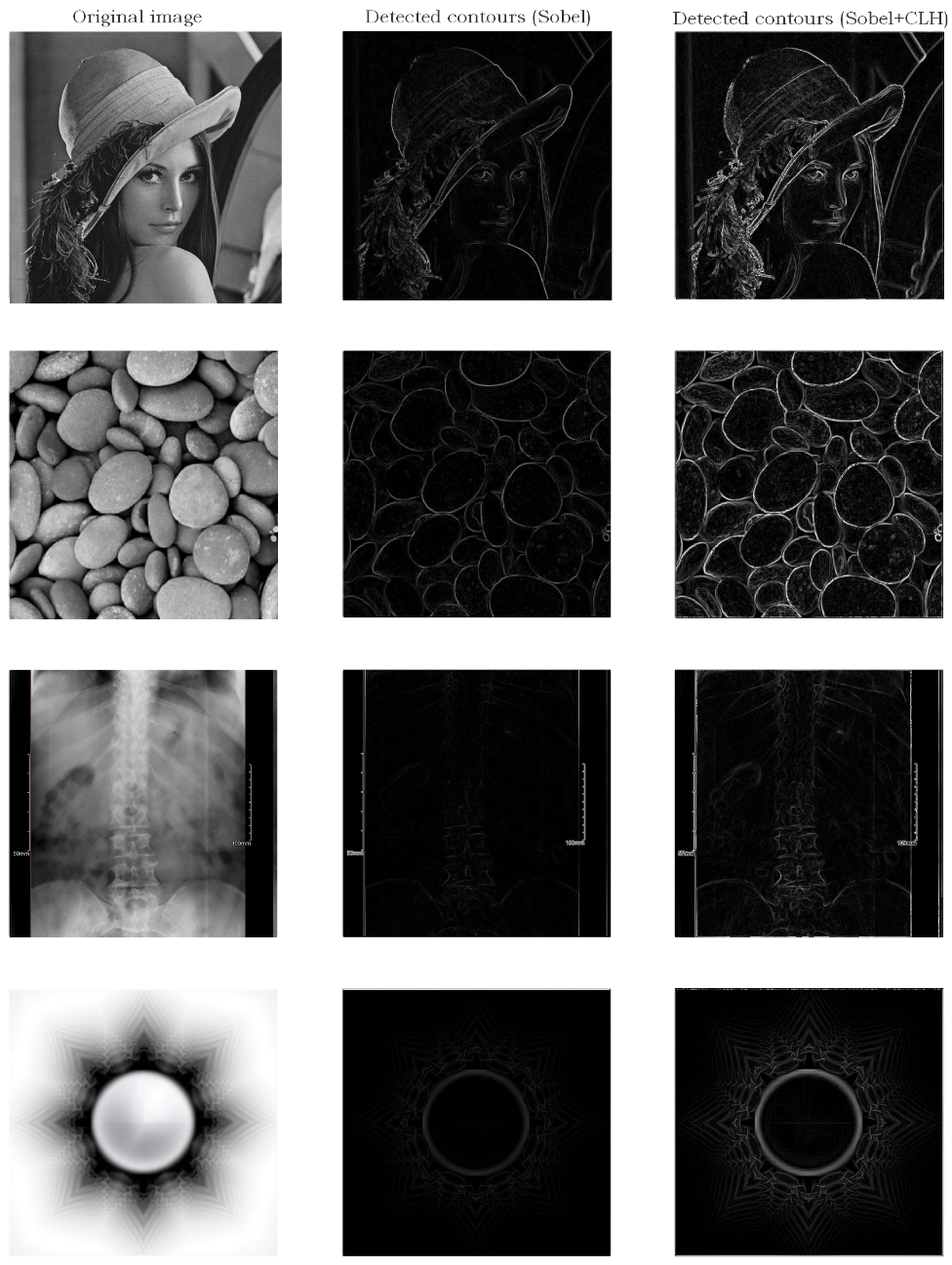
The application of the CLH matrix extends to improving weak contours in images, particularly in medical imaging, where clear depiction of contours is crucial. The matrix proves effective in enhancing the visibility of subtle contours that may be challenging to identify with traditional edge detection operators.

CONCLUSION

In this study, we introduced the concept of computing the Local Homogeneity Coefficient matrix (LCH) as a metric for evaluating the local texture structure. This calculation is founded on relationships with neighboring pixels, providing an assessment of local gray level homogeneity. Our findings indicate that this approach effectively regulates image regions based on gray level homogeneity, particularly discerning contours in well-homogeneous areas while enhancing faint or imperceptible contours. The method demonstrates sensitivity to variations in gray levels, proving adept at detecting contours between similar regions. In summary, CLH emerges as a promising solution for tasks such as texture analysis, contour detection, and noise reduction. Consequently, there are promising opportunities for applying our method in diverse domains, including remote sensing, medical imaging, computer vision, and beyond.

REFERENCES

1. Bashir Idris, Lili N. Abdullah, Alfian Abdul Halim, Mohd Taufik Abdullah Selimun (2022) Comparison of Edge Detection Algorithms for Texture Analysis on Copy-Move Forgery Detection Images. In: International Journal of Advanced Computer Science and Applications Vol 13, Issue 10, pp 155-156. Doi: 10.14569/IJACSA.2022.0131021.

2. Canny, J.F. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 8, 679–698.

3. F. M. Khellah, Texture classification using dominant neighborhood structure, IEEE Transactions on image Processing 20(11), 3270–3279 (2011).

4. Hanifi Majdoulayne (2005) Extraction de caracteristiques de texture pour la classification d’images Satellites, vol 19, pp 19-48. Doi: 10.3166/ria.19.633-659.

5. Jiangping He, Hongwei Ji, Xin Yang (2013) Texture analysis using local region contrast. Vol 22, Doi: 10.1117/1.JEI.22.2.023007.

6. Romero-Carazas R. Prompt lawyer: a challenge in the face of the integration of artificial intelligence and law. Gamification and Augmented Reality 2023;1:7–7. https://doi.org/10.56294/gr20237.

7. L. Li, C. S. Tong, and S. K. Choy, Texture classification using refined histogram, IEEE Transactions on image Processing, vol.19, no.7, pp.1371–1378, Jul. 2010.

8. Laurent Navarro, Guy Courbebaisse, Christian Roux. Une rédefinition des conditions aux limites de la méthode Lattice Boltzmann pour le débruitage d’images.

9. Gonzalez-Argote J. A Bibliometric Analysis of the Studies in Modeling and Simulation: Insights from Scopus. Gamification and Augmented Reality 2023;1:5–5. https://doi.org/10.56294/gr20235.

10. M. Subrahmanyam, R. P. Maheshwari, R. Balasubramanian. Local maximum edge binary patterns: A new descriptor for image retrieval and object tracking. Signal Processing, vol.92, pp.1467–1479, 2012.

11. Medina-Carnicer, R. Muñoz-Salinas, R. Yeguas-Bolivar, E. Diaz-Mas, L. A novel method to look for the hysteresis thresholds for the Canny edge detector. Pattern Recogn. 2011, 44, 1201–1211.

12. Meni Babakidi Narcisse (2022) Development of a gaussian filter for noise reduction in medical images. In : International Journal of Innovation and Applied Studies, vol. 32,  pp 295-300.

13. Gonzalez-Argote D, Gonzalez-Argote J, Machuca-Contreras F. Blockchain in the health sector: a systematic literature review of success cases. Gamification and Augmented Reality 2023;1:6–6. https://doi.org/10.56294/gr20236.

14. Milan Sonka, Vaclav Hlavac, Roger Boyle. Image processing analysis and machine vision (2013), pp 133-328.

15. Olivier Regniers. Méthodes d'analyse de texture pour la cartographie d'occupations du sol par télédétection très haute résolution: Application à la forêt, la vigne et les parcs ostréicoles (2014), pp 8-14.

16. Ouslimani Farida. Etude comparative des techniques de codage d’images en vue d’une segmentation (2018), pp 15-88.

17. Gonzalez-Argote J. Analyzing the Trends and Impact of Health Policy Research: A Bibliometric Study. Health Leadership and Quality of Life 2023;2:28-28. https://doi.org/10.56294/hl202328.

18. Qu Ying-Dong, Cui Cheng-Song, Chen San-Ben, Li Jin-Quan (2005) A fast subpixel edge detection method using Sobel–Zernike moments operator, vol 23 Doi: 10.1016/j.imavis.2004.07.003.

19. R. M. Haralick, I. Dinstein, and K. Shanmugam, Textural features for image classification, IEEE Trans. Syst. Man Cybern. 3(6), 610–621(1973).

20. Gonzalez-Argote J. Patterns in Leadership and Management Research: A Bibliometric Review. Health Leadership and Quality of Life 2022;1:10-10. https://doi.org/10.56294/hl202210.

21. S. Moore and R. Bowden. Local binary patterns for multi-view facial expression recognition, Computer Vision Image Understanding 115(2011) 541–558.

22. Saban Öztürk, Bayram Akdemir (2015) Comparison of Edge Detection Algorithms for Texture Analysis on Glass Production. In: World Conference on Technology, Innovation and Entrepreneurship, Elsevier, 195(2015)2675–2682.

23. Sana Sadeghi, Alireza Rezvanian, Ebrahim Kamrani (2012) An efficient method for impulse noise reduction from images using fuzzy cellular automata. In: AEU - International Journal of Electronics and Communications, vol 66, pp 772-229. Doi: 10.1016/j.aeue.2012.01.010.

24. Sonia Tabti. Modélisation des images par patchs pour leur restauration et leur interprétation. Applications à l’imagerie SAR, 2016.

25. Wiem Fourati, Mohamed Salim Bouhlel. Nouvelle Méthode pour le Débruitage d’images, 2007. In: 4rth International Conference: Sciences of Electronic, Technologies of Information and Telecommunications March 25-29, 2007 – Tunisia.

26. X. Huang, S. Z. Li, and Y. Wang, Shape localization based on statistical method using extended local binary pattern, in Proceedings of the Third International Conference on Image and Graphics, 2004, pp. 184–187.

FINANCING

The authors did not receive financing for the development of this research.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest.

AUTHORSHIP CONTRIBUTION

Conceptualization: Abdelhamid El Beghdadi; Mohammed Merzougui; Ahmad El Allaoui.

Research: Abdelhamid El Beghdadi; Mohammed Merzougui; Ahmad El Allaoui.

Drafting - original draft: Abdelhamid El Beghdadi; Mohammed Merzougui; Ahmad El Allaoui.

Writing - proofreading and editing: Abdelhamid El Beghdadi; Mohammed Merzougui; Ahmad El Allaoui.