Study of phosphoric acid slurry rheological behavior in the attack reactor and development of a model to control its viscosity using artificial intelligence

doi: 10.56294/dm202356

ORIGINAL

Study of phosphoric acid slurry rheological behavior in the attack reactor and development of a model to control its viscosity using artificial intelligence

Estudio del comportamiento reológico de la lechada de ácido fosfórico en el reactor de ataque y desarrollo de un modelo para controlar su viscosidad mediante inteligencia artificial

Ahmed Bichri^1,2, Hamid Mazouz², Souad Abderafi¹

¹MOSEM2PI, Ecole Mohammadia d’Ingénieurs, Mohammed V University of Rabat. Rabat, Morocco.

²OCP SA. Jorf Lasfar, Morocco.

Cite as: Bichri A, Mazouz H, Abderafi S. Study of phosphoric acid slurry rheological behavior in the attack reactor and development of a model to control its viscosity using artificial intelligence. Data and Metadata. 2023;2:160. https://doi.org/10.56294/dm2023160

Submitted: 12-08-2023 Revised: 27-10-2023 Accepted: 29-12-2023 Published: 30-12-2023

Editor: Prof. Dr. Javier González Argote

Guest Editor: Yousef Farhaoui

Note: paper presented at the International Conference on Artificial Intelligence and Smart Environments (ICAISE’2023).

ABSTRACT

This work aims to determine the rheological properties of the industrial phosphoric acid slurry and its behavior under the operating conditions of the phosphoric acid production process. For that, several experimental tests on the slurry were carried out, using a Rheometer (Anton Paar), which testing the effect of temperature and solid content. The results show that, for a fixed solids rate, the viscosity of the slurry decreases with temperatures from 75°C to 82°C and increases for temperatures above 82°C considered as the maximum temperature required by the process. This phenomenon is due to the morphological change of the gypsum which corresponds to the range of calcium sulfate hemihydrate formation. For a fixed temperature, the viscosity increases with increasing slurry solid content (31 % to 37 %). The viscosity increases with the shear gradient. Increasing the solid charge in the slurry increases its resistance to flow and movement. Thus, the slurry has a higher tendency to settle. A comparative study of four rheological models, Casson, Bingham, Ostwald and Herschel-Buckley, led to the selection of the Herschel-Bulkley model. This predicts the behavior of the phosphate slurry with a correlation coefficient of 99,9 % and a MAE less than 4 %. Overall, the results show that the threshold flow of the slurry is negligible, and its behavior is nonlinear. Thus, the slurry is a non-Newtonian fluid, with a dilatant rheological behavior. The various tests carried out enabled us to measure the viscosity of the phosphoric acid suspension for different solids contents and at different temperatures. The results obtained enabled us to study the rheological behavior and develop an artificial neural network model to control the viscosity of the slurry at the phosphoric acid attack tank.

Keywords: Rheological Behavior; Rheological Models; Phosphoric Acid; Viscosity; Slurry Solid Content.

RESUMEN

Este trabajo tiene como objetivo determinar las propiedades reológicas de la lechada industrial de ácido fosfórico y su comportamiento en las condiciones de operación del proceso de producción de ácido fosfórico. Para ello, se llevaron a cabo varias pruebas experimentales sobre el purín, utilizando un Reómetro (Anton Paar), en el que se comprobó el efecto de la temperatura y del contenido en sólidos. Los resultados muestran que, para una tasa de sólidos fija, la viscosidad del purín disminuye con las temperaturas de 75°C a 82°C y aumenta para temperaturas superiores a 82°C consideradas como la temperatura máxima requerida por el proceso. Este fenómeno se debe al cambio morfológico del yeso que corresponde al intervalo de formación del hemihidrato de sulfato de calcio. Para una temperatura fija, la viscosidad aumenta con el incremento del contenido en sólidos de la pasta (31 % a 37 %). Sólidos del Purín.La viscosidad aumenta con el gradiente de cizallamiento. El aumento de la carga sólida en el purín incrementa su resistencia al flujo y al movimiento. Por lo tanto, el purín tiene una mayor tendencia a sedimentar. Un estudio comparativo de cuatro modelos reológicos, Casson, Bingham, Ostwald y Herschel-Buckley, condujo a la selección del modelo Herschel-Bulkley. Éste predice el comportamiento de los lodos de fosfato con un coeficiente de correlación del 99,9 % y un MAE inferior al 4 %. En general, los resultados muestran que el flujo umbral de los purines es despreciable y su comportamiento no es lineal. Así pues, el purín es un fluido no newtoniano, con un comportamiento reológico dilatante. Los distintos ensayos realizados permitieron medir la viscosidad de la suspensión de ácido fosfórico para distintos contenidos en sólidos y a distintas temperaturas. Los resultados obtenidos nos permitieron estudiar el comportamiento reológico y desarrollar un modelo de red neuronal artificial para controlar la viscosidad de la suspensión en el tanque de ataque de ácido fosfórico.

Palabras clave: Comportamiento Reológico; Modelos Reológicos; Ácido Fosfórico; Viscosidad; Contenido en Sólidos del Purín.

INTRODUCCIÓN

To improve the efficiency of a process, it is necessary to study the behavior of the raw material and its transformations through rheology as a science of deformation and flow of the material to respond to the stresses or strains applied.^(1,2,3) Any mechanical system obeys a fundamental equation that establishes a relationship between the dynamic quantities responsible of the movement and the kinematic quantities describing this movement.⁽⁴⁾ Constitutive relationships, such as the relationships between stress, strain and time for a given test specimen, are used to link motion and forces to complete the description of the flow process and solve engineering problems.⁽⁵⁾ Based on these relationships, two categories of fluids can be distinguished, Newtonian and non-Newtonian fluids. Many fluids exhibit non-Newtonian behavior such as mineral suspensions, molasses, and phosphate pulp.^(6,7)

According to a study conducted on the grindability of industrial minerals in wet grinding used to produce ultrafine powders in various industries, it was found that it is influenced by the rheology of suspensions.⁽⁸⁾ In this study, they presented the different methods of characterizing the rheology of suspensions such as direct measurement by a rheometer and rheo-logical models describe the rheological behavior of suspensions for ultrafine grinding. It has been reported that the rheology of the suspension in grinding is very complex and influenced by many parameters such as solids concentration, particle size and distribution, particle shape, temperature, rotation, pH and the use of dispersants. It was also shown that the behavior of the suspension is Newtonian for low solid concentrations, and it changes to a non-Newtonian behavior with increasing solid concentration. Similarly, for particle size it was shown that there is an optimum ratio of coarse to fine particles of 40/60 at which the suspension was Newtonian with minimum viscosity. Temperature is the most important factor that strongly affects the apparent viscosity and yield strength of suspensions. It was revealed that controlling the rheological behaviors of suspensions in ultrafine grinding will increase throughput, energy efficiency and product fineness.

Oropeza et al.⁽⁹⁾ used rheology as a science of deformation and flow of material to study the behavior of the raw ma-terial and its transformations (Molasses; Mash; Fermentedmash; Incrustation and Impure bioethanol) and understand how materials respond to applied stresses or strains. It was found that the Newtonian model is suitable for Molasses at a temperature of 25°C and for an impure bioethanol solution at a temperature of 90°C. The Ostwald model is suitable for Mash at the temperature of 35°C.The pseudoplasticity decreases with increasing temperature towards Newtonian. The flow behavior index increased, and the rheological properties of the shear thinning fluid became weaker with in-creasing temperature. The other transformations fit the Herschel-Bulkley model well for the temperatures of 25°C and 90°C except for the impure bioethanol solution at the 90°C temperature. The apparent viscosity of molasses decreases with increasing temperature and decreasing shear rate, confirming the shear thinning behavior. Increasing the shear rate progressively untangles the arrangements of long chain molecules and helps overcome intermolecular resistance to flow. Abbasi et al.⁽¹⁰⁾ studied the non-linear rheological properties of kaolinite suspensions as a model fluid. The effect of particle geometry and slip velocity is part of this study. It was shown that kaolinite suspensions follow a Her-schel-Bulkley model, with yield stress increasing with concentration, irrespective of the type of kaolinite particles. The aspect ratio and asperity of the particles modify their sliding behavior, allowing the kaolinite network to have an ad-justable yield strength. For the phosphate industry, the rheological behavior of concentrated phosphate ore slurry has been studied for concentrations of 51 wt%, 54 wt%, 56 wt% and at a temperature of 25°C.⁽¹¹⁾ Note that this slurry is a suspension of insoluble particles of phosphate rock, the main raw material for fertilizers and phosphoric acid, in a continuous water phase). The authors have shown that this suspension has a non-Newtonian flow behavior and exhibits an elastic limit when the shear rate tends towards zero. Different grades and concentrations of phosphate ore were chosen for this rheological study. The results showed that the solid concentration in a solid-liquid mixture could be in-creased while maintaining a desired apparent viscosity.

Belbsir et al.⁽¹²⁾ studied the rheological behavior of the flow of phosphate pulp, transported by pipeline. Note that the transport of phosphate pulp by pipeline aims to optimize transport costs and increase production capacity. This mode of transport depends on the route and properties of the phosphate pulp. It has been shown that by dilution, the viscosity of the phosphate pulp decreases and the smaller the particle size in the pulp, the more viscous it becomes. It was also found that the phosphate suspension changes its pseudoplastic behavior to a Bingham behavior from the concentration of 46,03 % and changed its Bingham behavior to a dilatant behavior from the concentration of 38,45 %. The study was carried out for concentrations ranging from 34,24 % to 57,27 % and a temperature equal to 25°C. Various rheological models were tested to explain the behavior of the phosphate suspension, but only the Herschel-Buckley model was retained for the concentration range studied, indicating that the rheological behavior of the phosphate suspension is dilatant (p>1). Regarding modeling, it was concluded that the Herschel-Buckley model is suitable for describing the rheological behavior of the phosphate pulp and for calculating the apparent viscosity and the flow threshold for low concentrations (less than 38,45 %). The Bingham model is suitable for the range of concentrations between 34,24 % and 46,03 %. The Casson model is suitable for modeling the rheological behavior of the suspension and calculating the viscosity and yield point for the concentration range of 46,03 % to 57,27 %.

Boukhsib et al.⁽¹³⁾ studied the rheological behavior of phosphoric acid produced from Moroccan sedimentary phosphate rocks, for different P2O5 concentrations ranging from 18 to 54 % P2O5 and a temperature range from 22 to 80°C. The Herschel-Bulkley model fits all acids perfectly under the different conditions, with a regression coefficient R2 greater than 99,3 % and a mean absolute error less than 0,142. The same rheological behavior was observed when studying the phosphogypsum slurry resulting from the phosphoric acid production reaction.⁽¹²⁾ The study was carried out for temperatures ranging from 25°C to 80°C and for a concentration equal to 31 %. This study is very limited in relation to the dihydrate phosphoric acid production process, as the temperature range taken is far from that recommended for the correct operation of the phosphoric process (79°C to 82°C). Cooling the slurry of the samples studied from 80°C down to 25°C could have an impact on slurry characteristics and maturation. Similarly, in their study, the impact of solid content on slurry rheology was excluded.

Bichri et al.⁽¹⁴⁾ applied the artificial neural network method to predict the viscosity of phosphoric acid slurry by developing a model for predicting dynamic slurry viscosity as a function of influencing variables. The work consisted in studying the importance of three key operating parameters of the phosphoric acid production plant: temperature, solids content and shear stress. The study showed that, in terms of importance, the parameter with the greatest influence on viscosity is solid content, followed by shear stress, then temperature. The work concluded that the optimal topology is that of 3-5-1 and was obtained using Adam's algorithm and using the hyperbolic tangent as the activation function. The 3-5-1 model showed a minimum MAE and RMSE equal to 0,0429 and 0,068, respectively.

Saaidi et al.⁽¹⁵⁾ studied the prediction of dynamic viscosity of phosphoric acid slurry as a function of temperature, shear rate and solids content by testing three machine learning models, namely artificial neural network (ANN), gradi-ent boosting (GB) and random forest (RF) according to the evaluation of correlation and significance, the study shows that the GB algorithm gives the best prediction compared to RF and ANN, with a high correlation coefficient above 99 % and minimum MAE and RMSE values equal to 0,236 and 0,484, respectively. On the other hand, the performance of the RF algorithm comes after that of GB and well ahead of that of the ANN model. As for the influence of the param-eters studied on the viscosity of the phosphoric acid slurry, the study states that the most influential parameter on vis-cosity is the solid content, followed by shear stress and finally temperature.

It was concluded that the Heschel-Bulkley model is the most adequate to model the slurry behavior for the different temperatures with an R2 closest to 1, followed by the Ostwald, Casson and finally the Bingham. To this end, in this work, we will determine, first, the rheological behavior of the phosphate slurry based on an experimental study, taking into account the operating conditions of the process on the temperature and the solid content used in the operation of the industrial process. To determine their effects on the rheological behavior of the slurry. The results, of the rheological behavior and viscosity of the slurry, obtained will be exploited to obtain the most reliable model that will allow to describe the rheological behavior of the phosphate slurry in the operating conditions of the process. In this case, we will test the Casson, Bingham, Ostwald and Herschel-Bulkley models, to choose the most appropriate one for the slurry. On the other hand, we will compare the result of the effect of the solid content on the viscosity of the slurry determined experimentally with that found by theoretical models for verification.

In this work, we will carry out a parametric sensitivity analysis to study the rheological behavior of the slurry inside the phosphate etching unit. This analysis involves testing the effect of temperature and solid content, for intervals corre-sponding to the industrial phosphoric acid production process. Similarly, we will develop a model for predicting the viscosity of the phosphoric acid slurry based on ANN.

MATERIAL AND METHODS

Reactor description

The dilute phosphoric acid is produced at Unit E of Jorf Lasfar / OCP by the attack and filtration unit (JACOBS process). This production is based on thickened phosphate pulp, concentrated sulfuric acid (98,5 %), recycled phosphoric acid from two filters and sludge from the dilute phosphoric acid storage unit. These flows, rich in phosphoric acid, are recycled to the tank to recover the phosphoric acid. The attack produces a phosphate slurry composed of phosphoric acid and gypsum crystals. The latter are separated during filtration. The phosphate pulp composed mainly of calcium phosphate (Ca3(PO4)2), in the form of fluorapatite (Ca10(PO4)6F2) with at a solid content of 65 %, reacts with sulfuric acid and phosphoric acid in different compartments of the etching vessel (Figure 1). The latter is circular in shape and consists of 13 agitated compartments, 9 of which are in the attack tank and 4 in the maturation tank. The flow of the slurry is done through these compartments.

The main reactions taking place in the reactor are those between calcium phosphate, acids (phosphoric and sulfuric) and water, leading to the formation of phosphoric acid at a concentration of about 28 % mass. P2O5 and gypsum. Phosphate pulp also contains calcium fluoride (CaF) and other impurities whose content varies according to the quality of the rock. Many secondary reactions occur, leading to the formation of other by-products such as hydrogen fluoride (HF) and silicon tetrafluoride (SiF4). The heat balance of the chemical reactions taking place in the reactor results in an overall negative (exothermic) heat of reaction. The heat formed is dissipated by passing the slurry through a circulation loop via a vacuum cooler in a Flash Cooler. The cooled slurry is returned to the reactor's maturation tank, which consists of four similar compartments separated by baffles and equipped with agitators. Most of the slurry is returned to the attack tank via an overflow. A fraction of the slurry (≈1/25) continues its evolution in the ripening tank. Maturation of the slurry promotes the growth of gypsum crystals to increase the filterability of the slurry. The slurry is then directed to filtration. The gypsum formed in the reactor must crystallize to facilitate its subsequent separation, which is done with filters. Crystallization of gypsum is a phenomenon whereby calcium sulfate dihydrate organizes itself into an ordered structure, forming crystals.

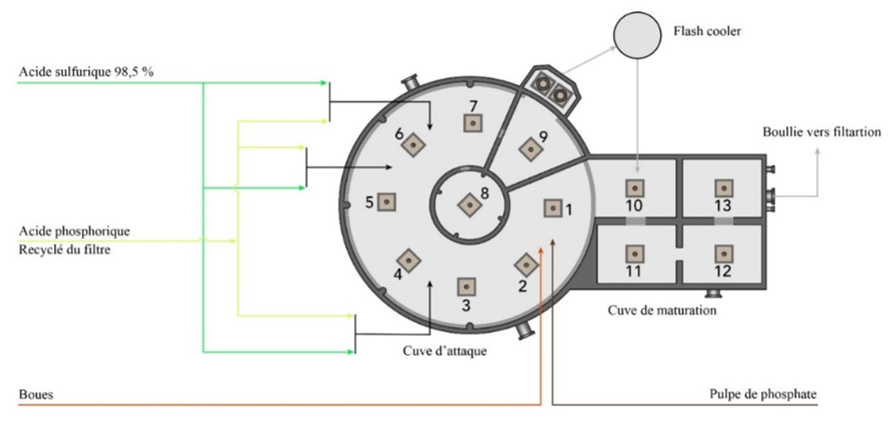
Figure 1. Phosphoric acid reactor (Jacobs) of the line E of Jorf Lasfar / OCP

In the maturation tank, crystallization is favored by reducing the turbulence due to agitation. Certain factors influence its speed (Temperature, Rate of supersaturation, Impurities, Viscosity, Agitation, P2O5 concentration).

The main operating parameters for controlling the performance and profitability of wet process phosphoric acid pro-duction are slurry temperature and slurry solids content, which should be maintained between 79 and 82°C and between 28 and 35 %, respectively. However, the rheological behavior of the slurry for these two parameters is also an important factor affecting phosphoric acid production.

Some impurities will slow down the development of the gypsum crystal. For the speed of crystallization, the time remains indirectly an important variable of the global process.

Experimental study

The rheological behavior of a slurry can be studied using a rheometer by directly measuring the relationship between shear rate and shear stress or apparent viscosity, which characterizes the time independent rheology of the slurry.⁽¹²⁾ An experimental study was conducted for the rheological measurement of the slurry, for temperatures ranging from 76 to 85 °C, the range covering the operating conditions of the phosphoric acid production process. The sample of the slurry was taken from the maturation tank related to the attack and filtration unit of the line E of Jorf Lasfar/OCP (JACOBS process). For the measurement of the solid content of the sample, a quantity of slurry of initial mass M2 is taken by a cleaned crucible of mass M1. The sample was filtered using a vacuum pump. The gypsum obtained by filtration was washed and after dried in an electric oven with the temperature maintained at a value of 60 °C to remove moisture. The mass of the dry solid, M3 was measured using an electronic balance with an accuracy of 0,01g. The solid content TS is determined by the following formula:

Ts= (M2-M1)/(M3-M1)×100 (1)

The rheological measurements were carried out using the experimental set-up shown in figure 2. This set-up consists of a rotating cylinder rheometer (Anton Paar), series MCR. It is equipped with a thermostat that allows the temperature of the device to be adjusted, particularly that of the cup, to the measurement value. The rheometer is equipped with a syn-chronous EC motor supported by an air bearing which deploys a synchronous movement without friction of the rotor inside, allowing more sensitive and therefore more precise movements. The rotor rotation varies from the highest to the lowest shear rate, i.e. a shear rate of 1000 s-1 to 1s-1. The device is connected to a computer that gives the record of shear stress (τ) as a function of shear rate (γ). The measurement procedure involves taking a 200 ml sample of the slurry and heating it under agitation using a heated magnetic stirrer, with a thermoprobe that allows the samples to be heated to the desired temperature. The temperature of the sample during heating is monitored with an infrared thermometer with an accuracy of ± 0,3°C. After checking the temperature of the cup and the rotor of the viscometer, the sample is poured into the cup and the measurement is launched in a fast way to avoid its cooling. A curve giving the shear stress (τ) as a function of the shear rate (γ) is drawn by the handling software of the device.

Figure 2. Experimental setup for rheological measurements

Rheological behavior model

In the literature, there are various rheological models describing the fluid flow curve, i.e. shear stress as a function of shear rate. Knowing the shear stress (τ) and the shear gradient (γ˙), the fluid viscosity is defined by the ratio of these two parameters:⁽¹⁶⁾

μ=τ/γ (2)

For a Newtonian fluid, this viscosity remains constant, showing a shear stress that is linearly proportional to the shear rate. However, a variation in viscosity as a function of these two parameters indicates that the fluid's behavior is non-Newtonian.⁽¹⁷⁾ To predict the rheological behavior of the slurry, four models can be distinguished, bearing in mind that they have been tested for phosphate pulp.⁽¹⁰⁾ The Casson model is often used to describe the rheological behavior of concentrated slurries, which exhibit pseudoplastic behavior with a stress threshold. Bingham's second model describes linear rheological behavior with a stress threshold. The third Ostwald model, also known as Power-Law, is often used to describe dilatant or pseudoplastic rheological behavior without threshold stress. The fourth Herschel-Bulkley model is a generalization of all the above rheological models. The equations of these different rheological models are as follows:

The casson model is often used to describe the rheological behavior of concentrated suspensions which have a pseudo-plastic behavior with a stress threshold, its equation is given by:

σ^1/2= (a.γ)^1/2+b (3)

With: viscosity is (a) and (b) =√((Yield stress)) γ: Shear rate and σ: Shear stress.

The second is Bingham model, it describes linear rheological behavior with threshold stress, its equation is:

σ= a.γ + b (4)

With: viscosity is (a), and (b) = (Yield stress).

The third is Ostwald model, also called Power-Law, is often used to describe rheological dilatant or pseudoplastic be-havior without threshold stress. Its equation is given by:

σ= a.γⁿ (5)

With: (a), is the coherence parameter, (n) is the behavior index of the flow.

The fourth model, the Herschel-Bulkley model, is a generalization of all the rheological models mentioned above. Its equation is given by:

σ= a.γ^p +b (6)

With: viscosity is (a), and (b) = (Yield stress), (p) is an exponent

Neural networks & Polynomial Regression methods

Artificial neural networks have emerged as an essential tool in machine learning and deep learning, achieving remarka-ble success across domains, including regression analysis, data classification. Artificial neural networks are inspired by the natural structure of neurons in the brain, with layers connected nodes. the Output of the network is the predicted results who are obtained by transmissions from the input layer of the input neurons to the output neuron layer via the hidden layer(s). To reduce the losses, an optimizer is used to estimate the weights and the biases of each connected neurons for all the layers connected. ANN training is accomplished through an iterative update of the weights and biases to find the optimal values for these hyperparameters that minimizes the error function between the real values and the predicted values. The predicted values of the ANN could be computed using an activation function.

In this work, our goal is to build an ANN to predict the sludge viscosity, to achieve this, we are implementing different experimentations using different number of neurons and different activations functions, also different optimizers.

The optimizers used in this work are the Adaptative moment estimation (Adam) and the stochastic gradient descent (SGD).

The activations functions are defined as follows:

ReLu(x)=max(0,x) (7)

tanh(x)= (e^x-e^(-x))/(e^x+e^(-x) ) (8)

leaky Relu(x)=max(αx,x) (9)

sigmoid(x)=1/(1+e^(-x) ) (10)

linear(x)=αx (11)

With x is the weighted sum of the neurons inputs the functions names of the output of the neuron, and α is constant fixed.

The model can be defined as follow, we denote the matrix X in IR^n.din a batch of n examples where each example has d inputs. for a MLP whose hidden has h hidden units (number of the neurons), we denote by H in IR^n.hthe outputs of the hidden layer, which are hidden representations, since the hidden and output layers are both fully connected, we have hidden-layer weights w⁽¹⁾ in IR^d.hand biases b⁽¹⁾in IR^1.hand output layer weights w⁽²⁾in IR^h.qand biases b^((2)) in 〖IR〗^(1.q). this allows us to calculate the outputs y_pred in IR^n.qof the one hidden layer ANN as follows:

H=Xw⁽¹⁾+b⁽¹⁾ (12)

ypred=Hw⁽²⁾+b⁽²⁾ (13)

In order to realize the potential of multilayer architectures, we need an activation function.

σ to be applied to each hidden unit following the affine transformation. In general, with activation functions in place, it is np longer possible to collapse our MLP into a linear model:

H=σ(Xw⁽¹⁾+b⁽¹⁾)(14)

ypred=Hw⁽²⁾+b⁽²⁾ (15)

In our case the q = 1 because we have dimension of the y_pred is one (the viscosity) the performance monitoring of the models assessed by The Mean squared Error, the Root Squared error and Pearson correlation coefficient. These indicators are defined as follows:

AE=1/n ∑ n(i=1)|y-ypred (16)

RMSE=√(1/n ∑n(i=1) (y-y_pred)2) (17)

=∑(y-ȳ)(y-ȳpred)/√(∑(y-ȳ) ∑(y-ȳpred) (18)

Where: n denotes the number of the observations.

y and y_pred denotes the observed sludge viscosity and the predicted by the models.

ȳ and ȳ_pred denotes the mean value of the y_pred and ȳ_pred.

The range of the neurons used for all the experimentations is fixed between 3 and 100 neurons.

The polynomial regression method is a regression algorithm that models the relationship between a dependently and independent variable x as n-the degree polynomial.

The polynomial regression equation is defined as below:

y=∑_(i=0)^n a_i x^i (19)

The need of polynomial regression in machine learning can be understood, when we apply a linear model on a linear dataset, then it provides us a good result.

The parameters studied in this approach is the maximal degree of the polynom, the optimizer used in this case is the Adam.

In this study, we seek to confirm the validity of the Herschel-Bulkley model to describe the rheological behavior of the slurry already identified by Belbsir et al.⁽¹⁶⁾. The rheological behavior of a fluid is obtained by plotting the variation of shear stress versus shear gradient for that fluid. We also seek to investigate the validity of the Herschel-Bulkley model for different values of slurry solid ratio. The formula of Herschel-Bulkley is:

σ=a.γ^p+b (6)

Where: σ, Shear stress; γ, Shear rate; a, b and p, Coefficients of the model.

The purpose is to use the experimental data to determine the exact values of the coefficients a, b and p using Matlab, to adapt equation (6) to the slurry under study, and thus establish a mathematical formula to represent the rheological behavior of the slurry. Secondly, these experimental data will be used to develop a model for predicting the viscosity of phosphoric acid slurry using machine learning methods, namely artificial neural networks.

RESULTS AND DISCUSSION

In this section we present the experimental results performed on the measurement of stress and shear rate. They were obtained with an error of 1,00 %. The viscosity is then deduced from these two parameters, for the different temperatures considered. The results obtained will be used for the validation of the model which allows to predict the rheological behavior of the slurry, as well as the confirmation of the variation of the viscosity with the rate of solid by the empirical formulas.

Effects of the parameters on the slurry rheological behavior

Rheological measurements were performed for a slurry sample with a solid content of 31,46 % and temperatures ranging from 76 to 85°C. The parameters to be studied and their ranges of variation were chosen considering the operating conditions of the phosphoric acid production process on an industrial scale. The approach is to use the industrial scale as a starting point for defining the elements to be studied. Shear stress and shear gradient data were collected by an Anton Paar MCR72 rheometer and recordings from Rheoplus / 32 V2.81 software.

The software was used to collect the variation in shear stress and viscosity as a function of the shear gradient from 1000 s-1 to 0 s-1 over 40 measurement points. The data obtained were used to plot the curves shown in figure 3 to visualize the evolution of the rheological behavior and viscosity of the slurry.

To observe the effect of temperature, measurements were repeated for the sample at different temperatures: 76°C, 79°C, 82°C and 85°C. Figure 3 shows all the results obtained.

This figure shows the effect of temperature on the rheological behavior of the slurry under the reactor temperature conditions. The variation of shear stress with shear gradient defines the rheological behavior of a fluid. Based on this rheological behavior, we distinguish two main families of fluids: Newtonian fluids whose behavior curve is a straight line passing through the origin, in the opposite case the so-called dilatant or pseudoplastic behavior.⁽⁵⁾

Each of figures (3.a) and (3.b) shows 4 curves in different colors. Each curve represents the relative results of the experimental test at a given temperature. Note that the same color code is used in both plots.

We can see that the slurry is a non-Newtonian fluid with a dilatant rheological behavior independently of the temperature and that its viscosity increases with the increase of the shear gradient. This confirms that the dilatant behavior observed by Belbsir et al.⁽¹⁶⁾ remains the same in the operating temperature range of the process.

From the curves of rheological behavior obtained, it is noted that the viscosity of the slurry decreases with the increase in temperature from 76 °C to a value of 82 °C, then for a temperature of 85 ° C we notice a sudden increase in the viscosity of the slurry (Figure 3). This change in viscosity variation with temperature above 82°C can be explained by a change in the morphology of the phosphogypsum (solid component of the slurry).⁽¹³⁾ Although the slurry behavior remains dilatant at 85°C, its viscosity increases remarkably. This change corresponds to a temperature value exceeding the operating limit recommended by the manufacturer (83°C). Above 83°C the calcium sulphate formed changes its form (hemihydrate) which is not always the case. (hemihydrate) which causes a change in its characteristics.

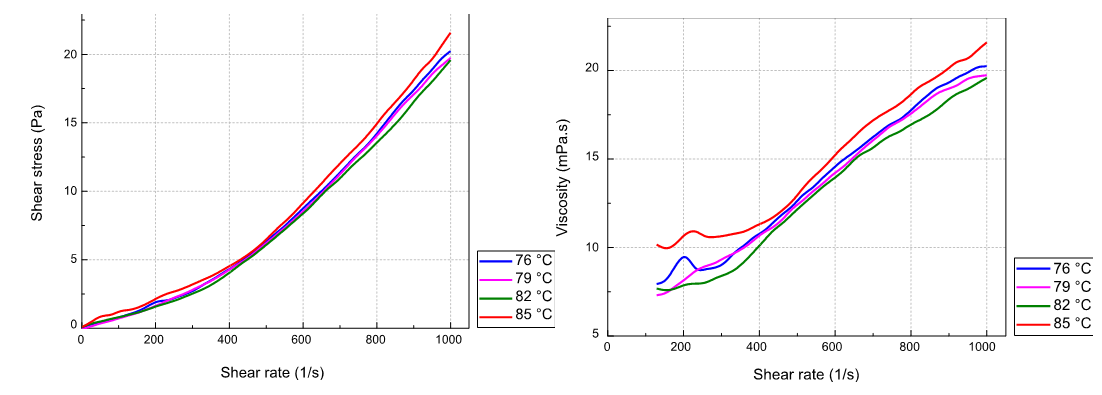
A B

Figure 3. Rheological behavior and viscosity variation of the slurry at different temperatures: (A) Rheological behavior; (B) Viscosity variation

The solid content is also an important parameter in the phosphoric acid production process. To study the effect of solid content on slurry rheology, two further samples were prepared from the parent sample and their solid rates are increased from 31,43 % to 35,02 % for the first and to 37,23 % for the second by extracting, from each, a quantity of phosphoric acid after the phosphogypsum has been settling. The new samples were stirred,

the tests were carried out on the new samples at temperatures ranging from 75°C to 85°C. Figure 4 shows the results for the variation in slurry rheology at different solid content levels given by (4.A), and the results for the variation in slurry viscosity at different temperatures.

The effect of solids content on slurry rheological behavior is shown in figure (4.A) at a fixed temperature of 80°C, corresponding to normal process operation. However, the effect of solid content on slurry viscosity is shown in figures (4.B), (4.C) and (4.D) at temperatures of 80°C, 75°C and 85°C respectively. To make the curves easier to read, the same color is used for different curves at a given temperature.

A B

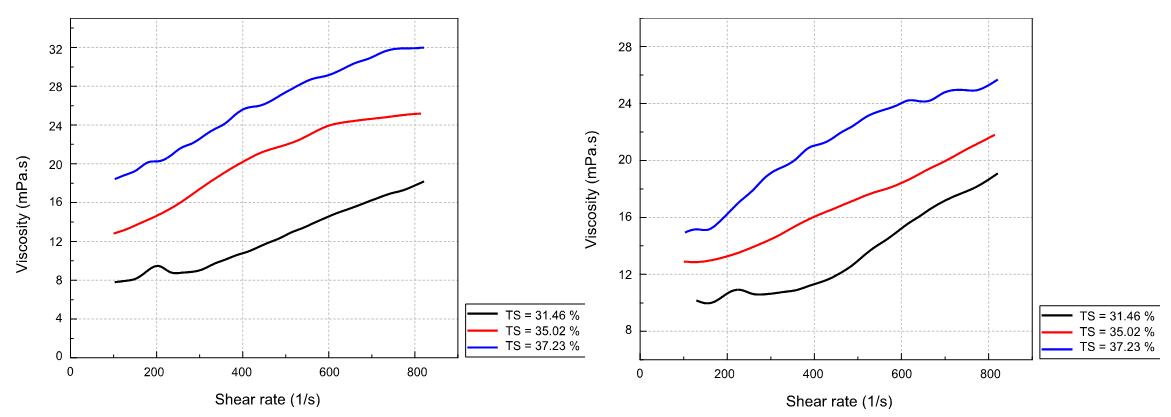
C D

Figure 4. Rheological behavior and viscosity variation of the slurry at different solid contents: (A) Slurry rheology behavior, at different solid contents, at T=80 °C; (B) Slurry viscosity, at different solid contents, at T=75 °C; (C) Slurry viscosity, at different solid contents, at T=80 °C; (D) Slurry viscosity, at different solid contents, at T=85 °C

From figures (4.B), (4.C) and (4.D) we deduce that the viscosity of the slurry increases with the solid content. The viscosity for a solid content of 35,02 % is greater for that corresponding to a solid content of 31,41 %; and it is even greater for the sample with 37,23 % of solid. So, we can see that the higher the solid content, the higher the viscosity, this is due to the increase in the load of the solution. Thus, the resistance to the deformation applied during the movement is greater, similarly, with a high solid content, the slurry tends to settle, which confirms the increase in its viscosity. According to the figure (4.A), it is also observed that the rheological behavior of the slurry is always dilatant for the different solid contents with a zero-flow threshold. The curve representing the rheological behavior moves upward keeping the same shape by increasing the solid content of the slurry. The higher the solids rate, the higher the viscosity of the slurry. When the temperature increases from 82°C to 85°C, the viscosity of the slurry as well as the mobility of the ions increases, which favors the growth of smaller crystals. At this temperature, the calcium sulfate crystals are no longer found in the form of gypsum but in the form of hemihydrate.⁽¹⁶⁾ These crystals are smaller and have a negative impact on filterability. Note that for a high solid concentration, there are many shocks that break up the crystals and become smaller and smaller. If the solid content is low, the distances that the ions must travel to integrate into an existing crystal lattice become too great for good growth, resulting in the formation of small crystals. The higher the solid content, the higher the viscosity of the slurry.

The viscosity of the slurry also increases with the shear gradient independently of the solid content as shown in figure 5. Increasing the solid content of the slurry causes a change in the temperature point at which the viscosity starts to increase with temperature. For the solid content 31,46 %, the viscosity increases from 82°C, however for the solid content 35,02 %, it starts to increase from 81°C, but for an even higher solid content 37,23 %, the viscosity increases beyond 80,5 °C. This can be explained by the change in the morphology of phosphogypsum. According to the previous results by exceeding a temperature of 82 °C, the viscosity of the slurry increases because of the formation of calcium sulfate hemihydrate. Therefore, with the increase of the solid content of the slurry, the effect of the formation of phosphogypsum hemihydrate on the viscosity of the slurry appears quickly as soon as the phenomenon starts due to the important quantity of solid in the slurry. However, for a low solid content, the solution is diluted, hence the impact of the change in crystal morphology on the viscosity is only observable after a fairly high temperature threshold. Thus, the effect of the solid content on the temperature threshold at which the viscosity starts to increase.

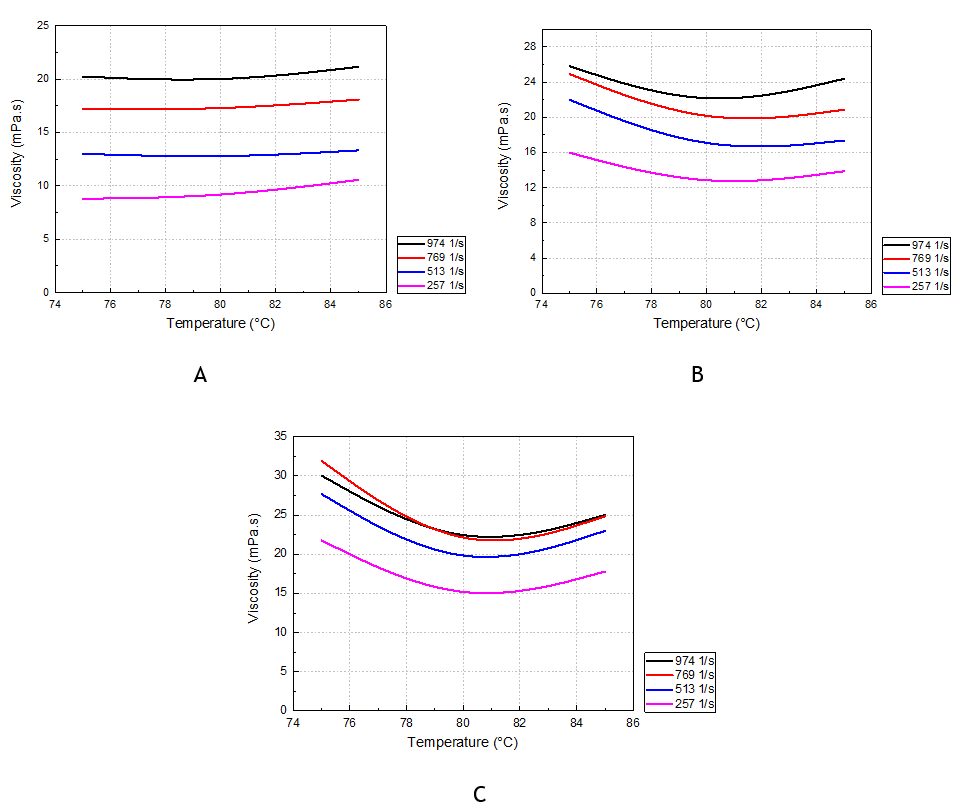
Figure 5. Slurry viscosity as a function of temperature at different shear rates: (A) Ts=31,46 %; (B) Ts=35,02 %; (C) Ts=37,23 %

Reliability of the Herschel-Bulkley rheological model

In this section, we will investigate the reliability of the Herschel-Bulkley rheological model to describe the rheological behavior of the slurry under the operating conditions of the phosphoric acid production process. To do so, we first determine the coefficients of each model equation for the slurry case, considering the operating conditions of the process and using the results of the experimental tests carried out on all the samples using the Matlab problem-solving software. Then analyze whether the result already established for the slurry remains valid.⁽¹⁶⁾

We consider the two samples of the slurry already prepared with solid contents respectively 31,46 % and 37,23 % and their experimental data. The rheometer used in the test allows us to generate the experimental data that are later exploited to fit the coefficients relative to the terms of each model equation.

The figures show the curve of the models at a temperature of 80°C (Figures 6 and 7). This temperature was chosen considering the mass percentage of P2O5 (28 %) and the real operating conditions of the reactor (JACOBS) of the E/Jorf /OCP line for the formation of calcium sulfate dihydrate.⁽¹⁶⁾ The results for the other temperature values and the different solid contents are summarized in table 1.

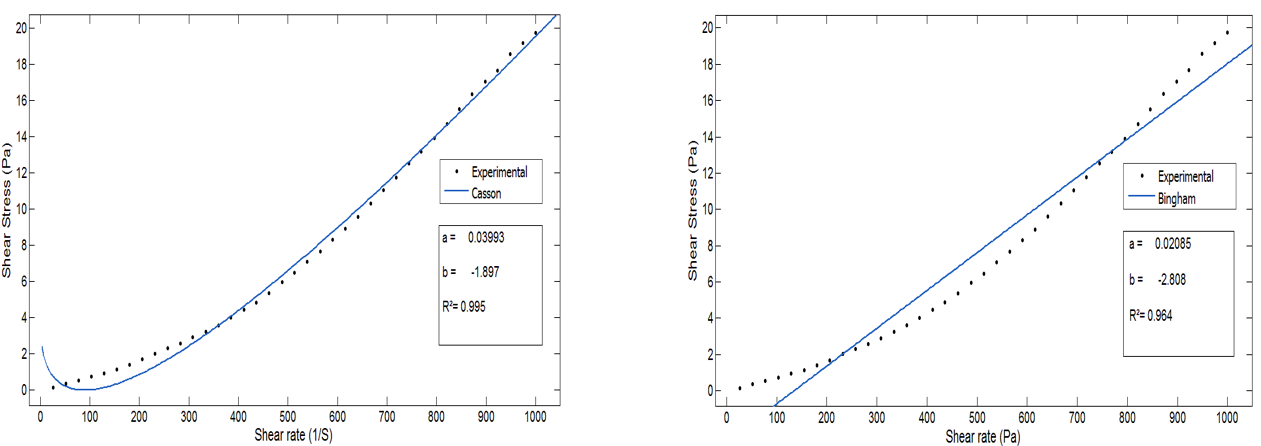
Figure 6. Comparison of measured values with values calculated by the Casson and Bingham Models at 80°C

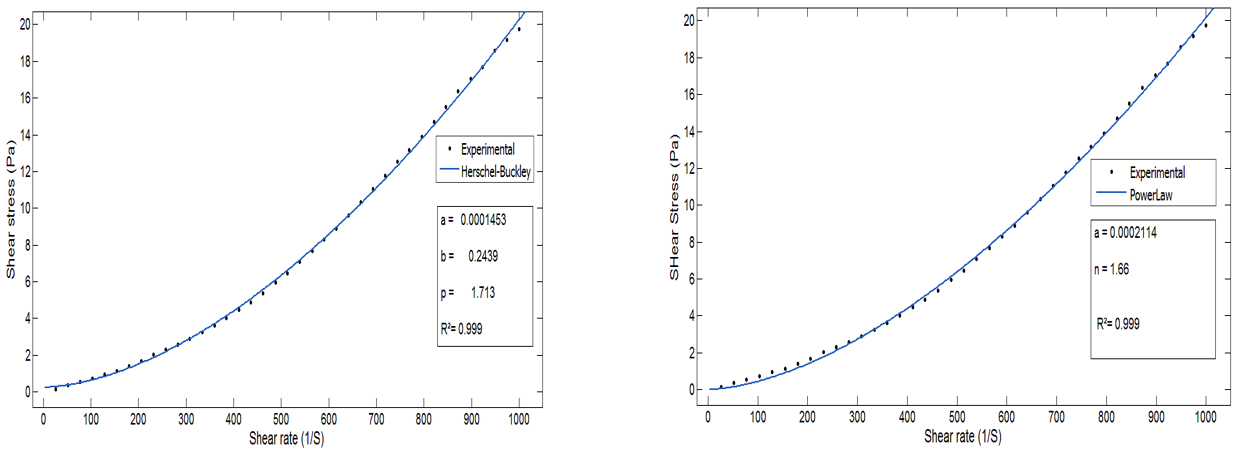
Figure 7. Comparison of measured values with values calculated by the Ostwald and Herschel-Bulkley Models, at 80°C

We find that the model that best describes the rheological behavior of the slurry is the Herschel-Buckley model, with a correlation coefficient of 99,9 % and an average relative error of no more than 4 %, for the different temperatures. This confirms that the Herschel-Buckley model is the most appropriate for modeling the rheological behavior of slurry.⁽¹²⁾ Moreover, considering and limiting itself to the temperature range relative to normal operation of the phosphoric acid production process, this model describes the rheology of the slurry with a correlation coefficient of 99,9 % instead of the 99,2 % already identified in the study by Belbsir et al.⁽¹²⁾. This model is also chosen based on the mean relative error of 4 %, while the Ostwald model has a correlation coefficient close to 1, but its mean relative error is high at around 9 %.

Table 1. Fitting results for different rheological models
Temperature (°C)	Casson model				Bingham model
Temperature (°C)	a (Pa.s)	b (Pa)	R²	MAE %	a (Pa.s)	b (Pa)	R²	MAE %
76	0,04099	-1,938	0,994	17,97	0,02115	-2,814	0,961	43,41
79	0,03993	-1,897	0,995	17,60	0,02085	-2,808	0,964	45,68
82	0,03967	-1,932	0,986	17,37	0,02023	-2,719	0,961	44,03
85	0,04207	-1,924	0,990	20,31	0,02177	-2,662	0,956	33,66
Temperature (°C)	Ostwald-power Law model				Herschel-Buckley model
Temperature (°C)	a (Pa.s)	b (Pa)	R²	MAE%	a (Pa.s)	b (Pa)	R²	MAE%
76	0,0002054	1,667	0,998	8,69	0,0001172	0,3646	1,747	0,999
79	0,0002114	1,66	0,999	7,70	0,0001453	0,2439	1,713	0,999
82	0,0001893	1,672	0,999	8,77	0,0001156	0,3085	1,742	0,999
85	0,0002514	1,644	0,997	11,98	0,00007968	0,7552	1,807	0,999

To confirm the suitability of the Herschel-Bulkley model for describing the rheological behavior of the slurry, we will this time use experimental data relating to sample 2 with a solids content of 37,23 %. The aim is to study the four rheological models already mentioned.

By plotting the experimental curves and approximating them by the various mathematical models, we obtain figures 8 and 9, which show the modeling graphs for the different models at a temperature of 80°C, corresponding to the operating value of the phosphoric acid production process (JACOBS). Model coefficients at different temperatures are given in table 2.

Table 2. Fitting results for different rheological models
Temperature (°C)	Casson model				Bingham model
Temperature (°C)	a (Pa.s)	b (Pa)	R²	MAE %	a (Pa.s)	b (Pa)	R²	MAE %
75	0,04356	-0,9294	0,9971	45,23	0,03381	-2,429	0,9929	68,87
80	0,02819	-0,8205	0,998	20,24	0,02094	-1,448	0,9905	50,03
85	0,03483	-0,8038	0,9989	22,00	0,02732	-1,921	0,9953	41,99
Temperature (°C)	Ostwald-power Law model				Herschel-Buckley model
Temperature (°C)	a (Pa.s)	b (Pa)	R²	MAE%	a (Pa.s)	b (Pa)	R²	MAE%
75	0,006433	1,234	0,9963	48,97	0,01311	-0,1899	1,26	0,9966
80	0,002934	1,281	0,9993	13,61	0,002624	0,1036	1,297	0,9993
85	0,005437	1,228	0,9984	26,16	0,007461	-0,4192	1,184	0,9986

Figure 8. Comparison of measured values with values calculated by the Casson and Bingham Models at 80°C

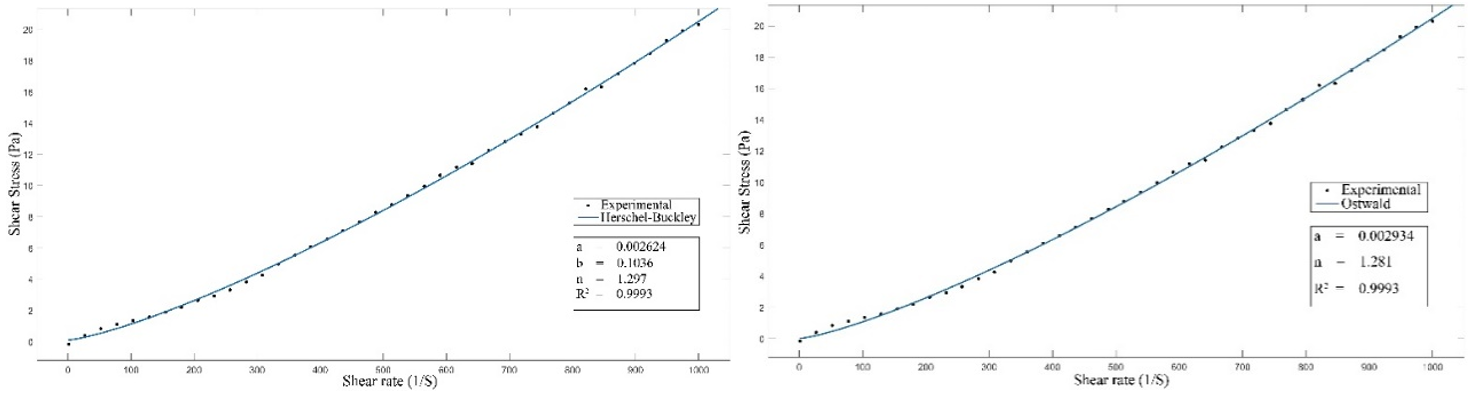
Figure 9. Comparison of measured values with values calculated by the Ostwald and Herschel-Bulkley Models at 80°C

The Herschel-Bulkley model remains the most appropriate for describing the rheological behavior of the slurry with a solid content of 37,23 % and at a temperature of 80°C. The correlation coefficient is (R2= 0,999), and the mean error 12,85 %. The Ostwald model with a (R2= 0,999) and an error of 13,61 %, then the Casson model with a (R2 = 0,998) and finally the Bingham model with a coefficient of (R2=0,9905). Thus, as already noted in part 1, the rheological behavior of the slurry remains the same irrespective of temperature and solids content. It should be noted that both the Casson and Bingham models always generate a negative b coefficient, meaning a negative yield stress. So, from a physics point of view, these two models cannot be used to describe slurry rheology. Similarly, for temperatures of 75°C and 85°C, the Herschel-Bulkley model also has a negative b coefficient, so it represents a negative yield stress. Moving away from the operating temperature (80°C) and for high solids contents, the rheological model that can describe slurry behavior is the Ostwald model.

ANN Model performance assessment

In this part, we seek to build an ANN to predict slurry viscosity, to achieve this we implement different experiments using different numbers of neurons and different activation functions, as well as a fixed optimizer for all cases.

To have a high accurate prediction with the real value observed of the target, we are launching 97 experiments, every experiment uses a fixed number of neurons in different activations functions as mentioned, and different optimizer. The dataset is split as 20 % for testing and 80 % for training, we are using as a preprocessing method: the standardization scale (this method shown a powerful impact in reducing the MAE and RMSE value and maximizing the coefficient correlation).

To discuss the resulted to search to an efficiency ANN to predict the target studied, the experiment as described try to search for right number of neurons and the activation function that performed well in reducing the MAE and RMSE and increasing the Pearson correlation coefficient.

Somes statistics tools are used to analyze to resulted parameters like the line plot and the scatter, the first one is used for visualizing the variation of errors (RMSE and MAE) in the different number of neurons and activations functions and the second one is used to visualization the Pearson correlation coefficient property.

The visualization bellow shows the variation of RMSE errors in different number of neurons and activations functions (Figure 10).

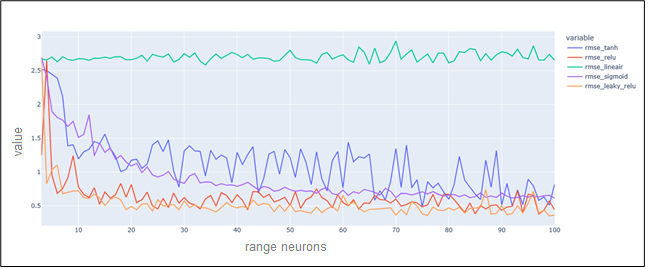
Une image contenant texte, ligne, Police, Tracé

Description générée automatiquement

Figure 10. RMSE variations for different numbers of neurons and activations functions

The visualization bellow shows the variation of MAE errors in different number of neurons and activations functions (Figure 11).

Une image contenant texte, Police, ligne, écriture manuscrite

Description générée automatiquement

Figure 11. MAE variations for different numbers of neurons and activations functions

The scatter visualization bellow to compare the predicted values by the model and the real values using the Pearson correlation coefficient (figure 12).

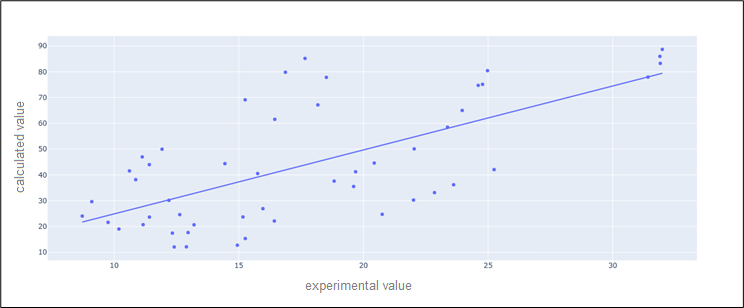
Une image contenant capture d’écran, ligne, Tracé, diagramme

Description générée automatiquement

Figure 12. scatter visualization to compare the predicted values by the model and the real values using the Pearson correlation coefficient

By interpreting all the figures, we can resume our results in the table below:

Table 3. Results resume with standardization in the case of Adam optimizer
Number of neurons	Preprocessing	MAE	RMSE	Pearson coefficient correlation	Number of hidden layers
99 neurons	With Standardization	0,26500	0,34991	0,669910	1

The experimentation shown that the best activation function for the first hidden layer in Our ANN is the Leaky ReLu. The standardization technique made a powerful impact in reducing the values of the MAE and RMSE. The results obtained when we ignore the Standardization is presented in the table below:

Table 4. Results resume without standardization in the case of Adam optimizer
Number of neurons	Preprocessing	MAE	RMSE	Pearson coefficient correlation	Number of hidden layers
99 neurons	Without standardization	2,48523	3,23583	-	1

The resulted parameter for the first hidden layer, are used in a second experimentation to study the behavior of the errors if we add a new hidden layer. the output result in this second experimentation shown that the errors MAE and RMSE also the Pearson coefficient correlation shown any behavior. so, we can conclude that the ANN neural network with one hidden layer is the best for our experimentation.

The visualization bellow shows the variation of RMSE errors in different number of neurons and activations functions using SGD optimizer.

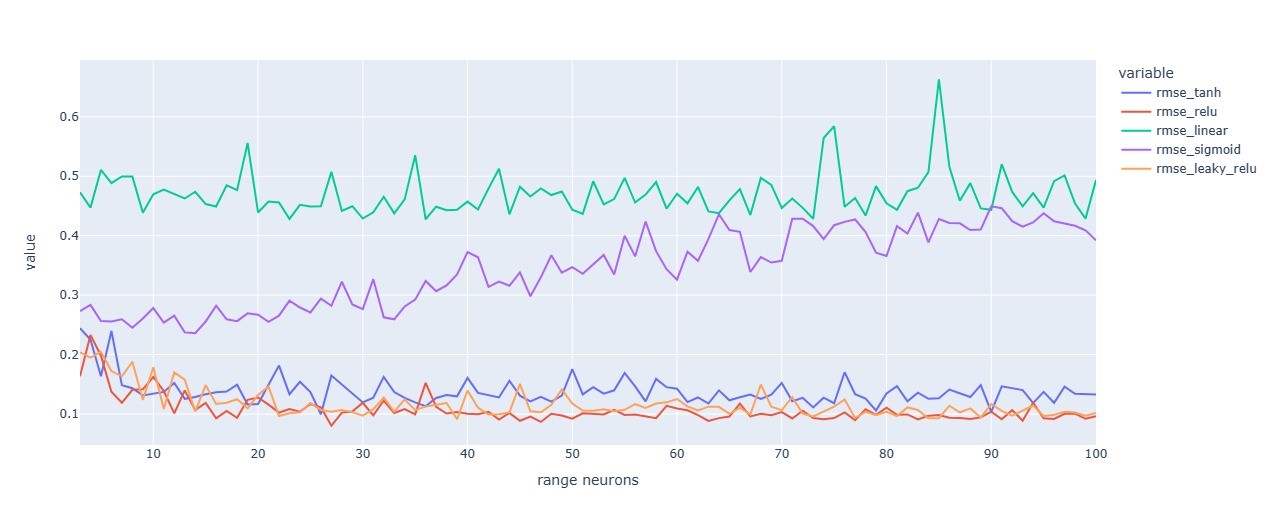
Figure 13. RMSE variations for different numbers of neurons and activations functions using SGD

The experimentation shown that the best activation function for the first hidden layer in Our ANN using SGD optimizer is the ReLu.

The scatter visualization bellow to compare the predicted values by the model and the real values using the Pearson correlation coefficient in the case of SGD optimizer.

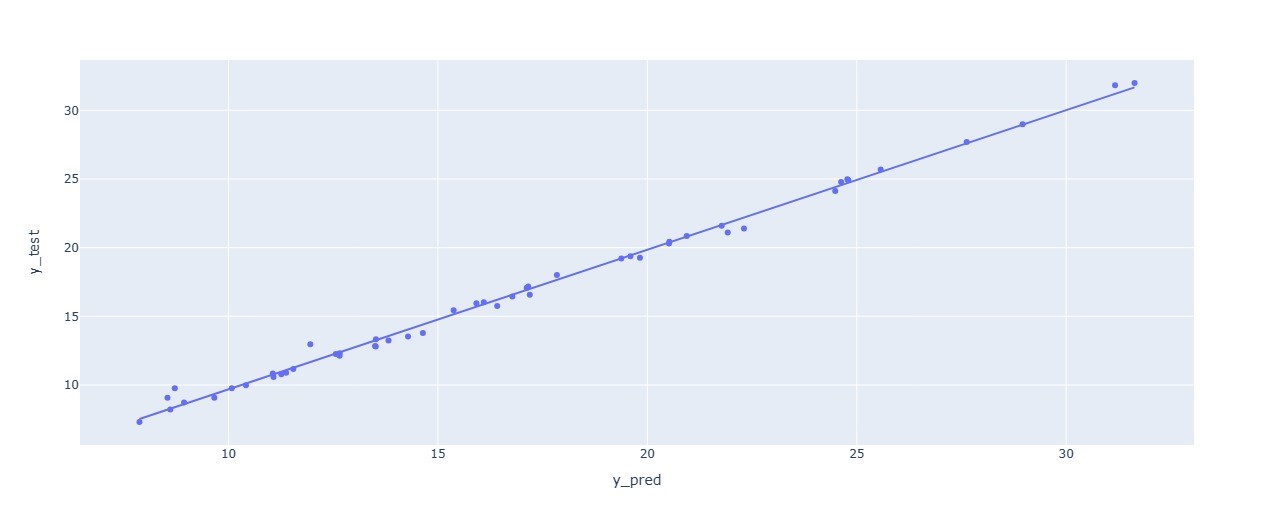
Une image contenant ligne, texte, Tracé, capture d’écran

Description générée automatiquement

Figure 14. Scatter visualization to compare the predicted values by the model and the real values using the Pearson correlation coefficient (optimizer SGD)

By interpreting all the results, the SGD optimizer made a powerful impact in reducing the values of the MAE and RMSE. The results obtained are presented in the table below:

Table 5. results resume with standardization in the case of SGD optimizer
Number of neurons	Preprocessing	MAE	RMSE	Pearson coefficient correlation	Number of hidden layers
27 neurons	Standardization	0,368323	0 481970	0,997840	1

Polynomial Regression methods

The same as ANN, in this case to accurate prediction value with the real value observed, we are launching 10 ex-periments, every experiment uses a different maximal degree for the polynom. The dataset is decomposed to 20 % for testing and 80 % for training, and we are not using any preprocessing technique. The difference between the polynomial Regression process and ANN process is the Polynomial Regression method experiment use the cross validation.

To discuss the resulted parameter, we are using different statistics tools as like the first experiment for ANN. The model performance indicators for these experiments are the same as the ANN (MAE, RMSE and the Pearson correla-tion coefficient).

The visualization bellow describes the variation of the errors (MAE and RMSE) in different degree of the Polynomial regression method (figure 15):

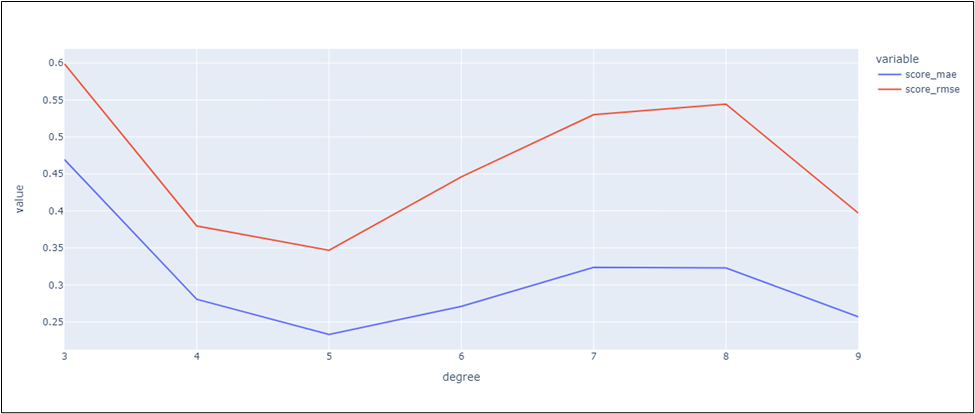
Figure 15. Variation of the Errors (MAE and RMSE) in different degree of the Polynomial regression methods

The scatter visualization bellow to compare the predicted values by the model and the real values using the Pearson correlation coefficient (figure 16).

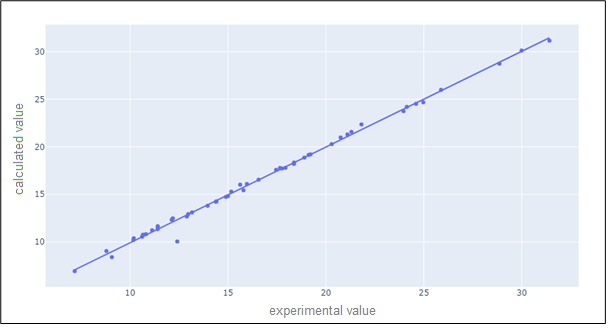
Une image contenant capture d’écran, texte, ligne, Tracé

Description générée automatiquement

Figure 16. Scatter visualization to compare the predicted values by the model and the real values using the Pearson correlation coefficient

By interpreting all the figures, we can conclude that the Polynomial Regression methods achieve minimal errors in the case of the degree equals a 5. The polynom regressor with the degree 5 had a Pearson correlation coefficient equal 0,9977249.

The resulted parameters in these experiments for these methods is presented bellow in the table:

Table 6. Resume of the MAE, RMSE and Correlation coefficient values in different degrees of the Polynomial regression in the presence of cross validation
Degree	RMSE	MAE	Correlation coefficient
3	0,598779	0,469549	0,9932296
4	0,379788	0,280571	0,9975221
5	0,346856	0,233018	0,9977249
6	0,446142	0,271050	0,9958608

The crosse validation made an impressive impact in reducing the Errors to the highest level. the table below resumes the variation of Errors for different degree:

Table 7. Resume of the MAE, RMSE and values in different degrees of the Polynomial regression in the absence of cross validation
Degree	RMSE	MAE
3	0,849521	0,540174
4	0,515134	0,330001
5	0,513553	0,291451
6	0,789740	0,427862

CONCLUSION

In this study, we carried out an experimental study to measure the stress and shear rate of the slurry taken from the ripening tank linked to the phosphoric acid production etching unit, with an experimental error of no more than 1 %. The results obtained enabled us, on the one hand, to observe that as temperature increases, viscosity decreases, up to a temperature of 82°C, beyond which we observed a sudden increase in viscosity. This change was interpreted as a change in phosphogypsum morphology. The higher the solid content, the more viscous the suspension, and the same variation was observed for the effect of shear rate on suspension viscosity. The effect of solids content on viscosity is related to the increase in frictional forces between solid particles, as well as to the increase in the suspension's resistance to flow. The temperature and solids content ranges chosen for this study correspond to the operating conditions of the phosphoric acid production process. To model rheological behavior, we compared experimental data with four empirical models (Casson, Bingham, Ostwald and Herschel-Bulkley). We concluded that the most appropriate model to represent the rheological behavior of the suspension is the Herschel-Bulkley model under the operating conditions of the phosphoric acid pro-duction process. On the other hand, we explored two distinct approaches, namely artificial neural networks (ANNs) and polynomial regression, to predict viscosity within the framework of our dataset. After a thorough analysis of the results and a comparison of the correlation coefficients between the two methods, it’s evident that the optimizer SGD used in ANN exhibits a closer correlation with the observed data, approaching the value of 1, and reduce the number of neurons in the first hidden layer to 27 neurons against the 99 neurons in the uses of Adam optimizer.

The table below summarizes the values of RMS (Root Mean Square), MAE (Mean Absolute Error), and the correlation coefficient from the previous experiments.

Table 8. MAE, RMSE and correlation coefficient in ANN method and polynomial regression
Methods	Number of neurons	Activations functions	RMSE	MAE	Correlation coefficient
ANN (SGD)	27	Relu	0,481970	0,368323	0,997840
ANN (Adam)	99	Leaky_relu	0,34991	0,26500	0,669910
Polynomial Regression (degree 5)	-		0,346856	0,233018	0,997729

This conclusion underscores the importance of judiciously selecting the prediction model based on the specific characteristics of the data. While artificial neural networks are powerful tools, the nature of the data can sometimes make other approaches, such as polynomial regression, more suitable. These results provide valuable insights to guide the choice of modeling methods in similar contexts, thereby contributing to the improvement of viscosity prediction accuracy.

REFERENCES

1. Roger I. Tanner, Engineering Rheology, second ed., Oxford Univer-sity Press, New York, 2000, pp. 1–29.

2. R.W.Whorlow, Rheological Techniques, second ed., Ellis Horwood,West Sussex (England), 1992, pp. 1–40.

3. Steffe, J.F., 1996. Rheological Methods in Food Process Engineering, second ed. P.E.FreemanPress, USA (Ph. D.)

4. Baudez 2001 “Rheology of aging, concentrated, polymeric suspensions: Application to pasty sewage sludges” Journal of Rheology.

5. He, M., Wang, Y. &Forssberg, E., (2004), “Slurry rheology in wet ultra-fine grinding of industrial minerals: a review”, Powder Tech-nology. Vol. 147

6. Gonzalez-Argote D, Gonzalez-Argote J, Machuca-Contreras F. Blockchain in the health sector: a systematic literature review of success cases. Gamification and Augmented Reality 2023;1:6–6. https://doi.org/10.56294/gr20236.

7. Seyssiecq, J.H. Ferrasse, N. Roche, State-of-the-art: rheological characteri-zation of wastewater treatment sludge, Biochemical Engi-neering Journal 16(2003) 41–56.

8. A.Peverea, G. Guibauda, E. Goina, E. van Hullebuscha, P. Lensb, Effects ofphysico-chemical factors on the viscosity evolution of anaerobic granularsludge, Biochemical Engineering Journal 43 (2009) 231–238.

9. Mingzhao. et al. “Slurry rheology in wetultra-fine grinding of industrial minerals: a review”, Powder Technology. Vol. 147 (2004).

10. Auza-Santiváñez JC, Díaz JAC, Cruz OAV, Robles-Nina SM, Escalante CS, Huanca BA. mHealth in health systems: barriers to implementation. Health Leadership and Quality of Life 2022;1:7-7. https://doi.org/10.56294/hl20227.

11. Gonzalez-Argote J. A Bibliometric Analysis of the Studies in Modeling and Simulation: Insights from Scopus. Gamification and Augmented Reality 2023;1:5–5. https://doi.org/10.56294/gr20235.

12. E. Oropeza-De la Rosa, L.G. López-Ávila, G. Luna-Solano, D. Cantú-Lozano, Bioethanol production process rheology. Industrial Crops and Products 106 (2017) 59–64

13. Abbasi Moud, A., Poisson, J., Hudson, Z. M., & Hatzikiriakos, S. G. (2021). Yield stress and wall slip of kaolinite networks. Physics of Fluids, 33(5), 053105.

14. Souhail Maazioui , Abderrahim Maazouz, Fayssal Benkhaldoun, Driss Ouazar and Khalid Lam-nawar. Rheological Characterization of a Concentrated Phosphate Slurry. Fluids 2021, 6, 178. https://doi.org/10.3390/fluids6050178.

15. Romero-Carazas R. Prompt lawyer: a challenge in the face of the integration of artificial intelligence and law. Gamification and Augmented Reality 2023;1:7–7. https://doi.org/10.56294/gr20237.

16. Hamza Belbsir, Khalil El-hami, Aziz soufi . Study of the Rheological Behavior of the Phosphate-Water Slurry and Search, for a Suitable Model to Describe its Rheological Behavior. International Journal of Mechanical & Mechatronics Engineering IJMME-IJENS Vol:18 No:04 , 2018

17. Boukhsib, L. Khamar, M. S. Kadiri, K. Khallaki and L. Omari. Rheological behavior modelling of phosphoric acid produced from Moroccan phosphate rocks . Indian Chemical Engineer, 27 avril 2022.

18. Castillo-Gonzalez W. Charting the Field of Human Factors and Ergonomics: A Bibliometric Exploration. Health Leadership and Quality of Life 2022;1:6-6. https://doi.org/10.56294/hl20226.

19. Ahmed Bichri, Afaf Saaidi, Souad Abderafi, Application of Artificial Neural Network to predict phosphoric acid slurry viscosity, IEEE, 2022 5th International Conference on Networking, Information Systems and Security: Envisage Intelligent Systems in 5g//6G-based Interconnected Digital Worlds (NISS)

20. Afaf Saaidi, Ahmed Bichri, Souad Abderafi. Efficient machine learning model to predict dynamic viscosity in phosphoric acid production, Results in Engineering, https://doi.org/10.1016/j.rineng.2023.101024.

21. Hamza Belbsir, Khalil El-hami, Hamid Mazouz, Study of the Rheological Behavior of Phosphate Slurry and Its Derivatives Products. International Conference on Advanced Intelligent Systems for Sustainable Development (2020).

22. Gonzalez-Argote J. Patterns in Leadership and Management Research: A Bibliometric Review. Health Leadership and Quality of Life 2022;1:10-10. https://doi.org/10.56294/hl202210.

23. Iman Kazemi, Mohammad Sefid, Masoud Afrand. A novel comparative experimental study on rheological be-havior of mono & hybrid nanofluids concerned graphene and silicanano-powders: Characterization, stability and viscosity measurements. Powder Technology 366 (2020) 216–229.

ACKNOWLEDGEMENT

The authors gratefully acknowledge support provided by OCP Group.

FINANCING

The authors did not receive financing for the development of this research.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest.

AUTHORSHIP CONTRIBUTION

Conceptualization: Ahmed Bichri; Hamid Mazouz; Souad Abderafi.

Research: Ahmed Bichri; Hamid Mazouz; Souad Abderafi.

Drafting - original draft: Ahmed Bichri; Hamid Mazouz; Souad Abderafi.

Writing - proofreading and editing: Ahmed Bichri; Hamid Mazouz; Souad Abderafi.