Methods and algorithms of optimization in computer engineering: review and comparative analysis

doi: 10.56294/dm2024443

REVIEW

Methods and algorithms of optimization in computer engineering: review and comparative analysis

Métodos y algoritmos de optimización en ingeniería informática: revisión y análisis comparativo

Volodymyr Yakhno¹ *, Vadym Kolumbet² *, Petar Halachev³ *, Vladyslav Khambir⁴ *, Ruslan Ivanenko⁵ *

¹Kyiv National University of Technologies and Design, Department of Computer Science, Faculty of Mechatronics and Computer Technologies. Kyiv, Ukraine.

²National Technical University of Ukraine “Igor Sikorsky Kyiv Polytechnic Institute”, Department of Software Engineering for Power Industry, Educational and Scientific Institute of Atomic and Thermal Energy. Kyiv, Ukraine.

³University of Chemical Technology and Metallurgy, Department of Informatics. Sofia, Bulgaria.

⁴CapitalOne, Principal Software Engineer. McLean, VA, USA.

⁵The Ukrainian Scientific and Research Institute of Special Equipment and Forensic Expertise. Kyiv, Ukraine.

Cite as: Yakhno V, Kolumbet V, Halachev P, Khambir V, Ivanenko R. Methods and algorithms of optimization in computer engineering: review and comparative analysis. Data and Metadata 2024; 3:443. https://doi.org/10.56294/dm2024443

Submitted: 07-01-2024 Revised: 10-04-2024 Accepted: 16-07-2024 Published: 17-07-2024

Editor: Adrián Alejandro Vitón Castillo

ABSTRACT

Introduction: the main areas of application of artificial intelligence for algorithmic analysis and optimization of information flows in tasks of multiparametric diagnostics by means of computer engineering are considered. The issues of globalization of all areas of humanitarian, scientific, technical and engineering activities of human society are considered. It is noted that the common denominator of all directions is information flows. The main tools for their management and algorithmic analysis are multi-parametric methods of artificial intelligence.

Method: one of its most relevant areas has been highlighted - the use of evolutionary algorithms in combination with modern diagnostic systems based on computer engineering. The possibility of using intelligent analysis of data from biophysical laser systems in assessing the state of “living matter” - the biological media of the human body - is considered.

Results: through algorithmic optimization, a set of new cancer detection markers was determined: the statistical parameters of optical anisotropy maps wavelet coefficients linear distributions - the differences between these markers lie in the range from 4 to 20 times; the asymmetry of the wavelet coefficients autocorrelation function - the differences between these markers lie within two orders of magnitude; for normal state, the wavelet coefficients distributions are multifractal; for prostate cancer, the distributions of the wavelet amplitude coefficients are multifractal.

Conclusions: a comparative study of the algorithmic optimization of differences of cancer through the use of multiparametric statistical, correlational, fractal and wavelet analysis of polarization tomograms of optical anisotropy of blood layers of donors and prostate cancer sicks is presented.

Keywords: Search Algorithms; Multi-Agent Optimization; Multi-Parameter Diagnostics; Cancer.

RESUMEN

Introducción: se consideran las principales áreas de aplicación de la inteligencia artificial para el análisis algorítmico y la optimización de los flujos de información en tareas de diagnóstico multiparamétrico mediante ingeniería informática. Se consideran las cuestiones de la globalización de todos los ámbitos de las actividades humanitarias, científicas, técnicas y de ingeniería de la sociedad humana. Se observa que el denominador común de todas las direcciones son los flujos de información. Las principales herramientas para su gestión y análisis algorítmico son los métodos multiparamétricos de inteligencia artificial.

Método: se ha destacado una de sus áreas más relevantes: el uso de algoritmos evolutivos en combinación con modernos sistemas de diagnóstico basados en la ingeniería informática. Se estudia la posibilidad de utilizar el análisis inteligente de datos procedentes de sistemas biofísicos láser para evaluar el estado de la «materia viva», es decir, los medios biológicos del cuerpo humano.

Resultados: mediante la optimización algorítmica, se determinó un conjunto de nuevos marcadores de detección del cáncer: los parámetros estadísticos de las distribuciones lineales de los coeficientes de wavelet de los mapas de anisotropía óptica: las diferencias entre estos marcadores se sitúan en el intervalo de 4 a 20 veces; la asimetría de la función de autocorrelación de los coeficientes de wavelet: las diferencias entre estos marcadores se sitúan dentro de dos órdenes de magnitud; para el estado normal, las distribuciones de los coeficientes de wavelet son multifractales; para el cáncer de próstata, las distribuciones de los coeficientes de amplitud de wavelet son multifractales.

Conclusiones: se presenta un estudio comparativo de la optimización algorítmica de las diferencias del cáncer mediante el uso del análisis multiparamétrico estadístico, correlacional, fractal y wavelet de los tomogramas de polarización de la anisotropía óptica de las capas sanguíneas de donantes y enfermos de cáncer de próstata.

Palabras clave: Algoritmos de Búsqueda; Optimización Multiagente; Diagnóstico Multiparámetro; Cáncer.

INTRODUCTION

One of the main and dominant features of the development of humanity is the globalization of all areas of its activity, starting from political, social, economic, ecological, scientific and technical and many others.^(1,2)

The common denominator of all the diversity of such processes is information flows in the form of a wide range of databases. Among them, the most common are huge volumes of digital, text and graphic information, audio and video information, which dynamically change and qualitatively transform.^(3,4,5,6)

The specified information bases make up the input arrays of data for processing using modern computer engineering tools.

An important aspect of such processing is the availability of not only powerful high-speed processors, but also a complex of modern algorithmic approaches to intelligent analysis of information databases.⁽⁷⁾

The newest toolkit for processing the modern “sea of information” is the formation and effective functioning of the latest direction in informatics using the principles of neural networks - artificial intelligence (AI).^(3,4,5,6)

AI ideology correlates well with globalization processes and represents a complex information system, which is primarily aimed at creating the latest algorithms for processing databases. They are aimed at recognition, training, and the adoption of certain (management, diagnostic, etc.) decisions.^(8,9)

One of the main tools of AI is the development of expert systems. The main goal of such systems is to create such devices that are capable of analytically evaluating a problem like a person, distinguishing the main ones and making a conscious conclusion.^(5,6,10,11)

The main difficulty in implementing this paradigm is that in most cases the algorithm for solving the task is unknown in advance. In connection with this, a whole complex of various database processing algorithms is being intensively developed within the framework of AI.

The so-called evolutionary algorithms are one of the most relevant in the study of the environment surrounding us, its “living matter”. First of all, they are of undeniable interest for the biological, medical, and ecological fields of research into living matter at the micro (molecules, cells) and macro levels (organisms, environment, society) of its organization.⁽¹²⁾

The obtained algorithmic information is the basis for the formation of a number of computers engineering diagnostic systems that implement the latest principles of multiparameter diagnostics of the morphological, biochemical, polycrystalline structure of complex biological objects, including the human body.

Achieving such a goal is definitely relevant not only for various fields of practical medicine, economics, social activity, but also for fundamental algorithmic tasks from evolutionary to genetic programming.^(1,2,3,4,13)

To optimize the specified algorithmic diversity, the task of minimization is objectively relevant - identifying the most relevant and significant for achieving the ultimate goal of intelligent processing of data about living matter. Based on this, it is necessary to develop search algorithms that highlight the most important (diagnostic) information about “living” objects.⁽¹⁴⁾

The information obtained within the framework of machine learning will be evaluated using flexible statistical or other algorithms that will provide a number of objective criteria for characterizing a set of parametric object data.^(8,9,10)

The specified objectification of the results of machine learning should be carried out by means of global optimization, which, with the help of numerical analysis, will provide the necessary diagnostically relevant data minimization.^(11,15)

One of the options for the implementation of such a process can be linear programming. On this basis, the possibilities of finding a set of diagnostically optimal relationships between a set of data on the structure of living matter and a set of its numerical parameters open up.

It should be noted that obtaining information about living objects in the form of medical images, including the most convenient for the researcher optical ones, is the most informative.

Each such image is a multi-parameter information database about the diagnosed object. Such data are encoded in the spatial distributions of photometric, spectral, polarization and correlation characteristics of electromagnetic radiation.

This circumstance necessitates the development of a wide class of computer engineering diagnostic systems for the formation of optical images of biological objects - microscopic, polarimetric, tomographic, holographic. In addition, the “high” information capacity complicates the task of optimizing the algorithmic processing of various optical image parameters. Based on this, a complex algorithmic approach to the objectification of optical databases for their intellectual processing with the aim of producing an adequate diagnostic conclusion is relevant.

In our work, an example of complex statistical, correlational, fractal and wavelet algorithmic intelligent optimization of the data of a modern system of laser matrix tomography of the supramolecular structure of human blood films is described and characterized presented and analyzed in order to develop new criteria for early cancer diagnosis.

METHOD

The main information array in our work is a set of birefringence parameters (T(m×n)) of supramolecular protein networks of dehydrated human blood layers of donors and prostate cancer sick directly measured in the location of the laser polarization tomography.^{(16,17,18,19,20,21)}

Here we provide a brief summary of the laser polarization tomography technique. Two groups of samples of dehydrated blood films were studied. The first group - healthy donors (12 samples), the second group - patients with prostate cancer (12 samples).

A Mach-Zehnder polarization interferometer was used as a measuring platform. Here, using the algorithm of two-dimensional digital Fourier transform of interference patterns, the field of complex amplitudes of experimental samples was restored. On this basis, polarization tomograms were reconstructed.

In figure 1 presents examples of polarization tomograms T(m×n) of blood films.

Comparative analysis of T(m×n) polarization tomograms revealed:

· Coordinate, structural and scale heterogeneity of distributions T(m×n).

· The visual similarity of T(m×n) maps and the absence of characteristic differential signs of pathology.

Thus, to identify the pathological condition of the prostate according to the given information base T(m×n), we consistently used a chain of algorithms that characterize:

Figure 1. Polarization tomograms of blood films. Normal (1) and prostate cancer (2)

1. Statistical parameters (moments of the 1st - 4th orders ).

2. Autocorrelation functions and statistical moments of.

3. Multifractal parameters - logarithmic dependence of autocorrelation power spectra.

4. Scaling or wavelet structure (wavelet transform amplitude maps).

Statistical analysis

For the objective characteristics of T(m×n) tomograms, the central statistical moments - (U₁ - average),(U₂ - variance), (U₃ - asymmetry) and (U₄ - kurtosis) were calculated.^{(14,15,16,17,18)}

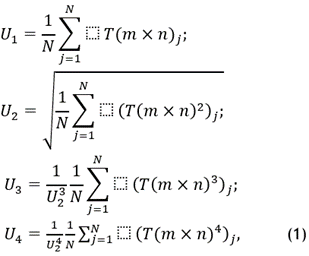
Where N is pixels quantity.

Correlation analysis

To calculate the autocorrelation function ACF(∆x) of the T parameters linear distribution following expression is used:

Here ∆x=1 pix. Analogues for direction y:

Fractal analysis

Fractal evaluation of large-scale self-similarity of T(m×n) distributions include the following steps:⁽²¹⁾

· Calculation of power spectra (SP(T(m×n))).

· Calculation of Log-Log distributions of power spectra LogSP(T(m×n))-Log(ν), where ν is the spatial frequency, is the scale of the local domain of the optical anisotropy of the blood film in the tomogram T(m ×n).

· Distributions LogSP(T(m×n))-Log(ν) were approximated using the least squares method.

· The slope angles of the approximating curve L(θ) were determined.

· The presence and length of J linear sections L(θ) were analyzed.

· If the length J lies within 2-3 scales in geometrical size d of the domains of the tomogram T(m×n), then the corresponding distributions are considered fractal.

· If there are several linear sections - T(m×n) distributions are multifractal.

· If there are no linear sections, the T(m×n) distributions are random.

We used algorithms (1) for quantitative characterization of LogSP(T(m×n))-Log(ν) distributions.

Wavelet analysis

Wavelet analysis is based on the analytical transformation of azimuth or ellipticity distributions using a scanning soliton-like function (wavelet ) with a change in half-width (“scale” a) and scanning coordinate b.^(20,21)

The continuous wavelet transforms of the polarization distribution Υ(x) is determined.

In our work, we used the next MHAT wavelet function:

DISCUSSION

Statistical approach

Table 1 presents the statistical analysis data by algorithms (1) of polarization tomograms T(m×n) of two representative samples (33 samples each) blood from control group 1 (normal) and experimental group 2 (prostate cancer).

Within each group, for each of the central statistical moments (U_i=1;2;3;4) its average (U_i=1;2;3;4) and root mean square deviation (±2σ_i=1;2;3;4).

Table 1. Statistical parameters of tomograms T(m,n)
(U_i=1;2;3;4)	Group 1	Group 2
(U_i=1×10^-3)	0,77±0,05	0,73±0,04
(U_i=2×10^-3)	0,24±0,02	0,21±0,02
(U_i=3)	0,88±0,06	0,94±0,06
(U_i=4)	1,05±0,07	1,13±0,08

The analysis of the obtained data did not reveal significant differences (~10 %) between the U_i=1;2;3;4) values, which characterize the tomograms of the blood films birefringence from both groups.

Correlation analysis

The next step of algorithmic optimization was the correlation analysis (ratio (2),(3)) of coordinate distributions T(m×n), figure 2 and figure 3.

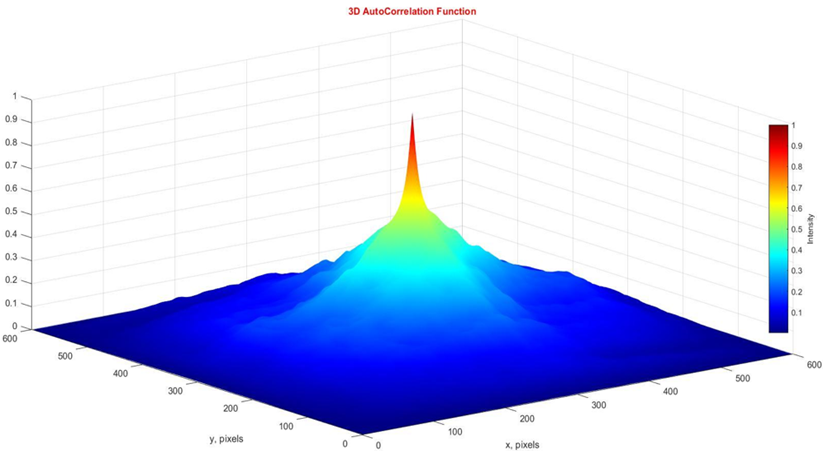
Figure 2. Two-dimensional autocorrelation function ACF(x,y) of the tomogram T(m×n) of blood sample from control group 1

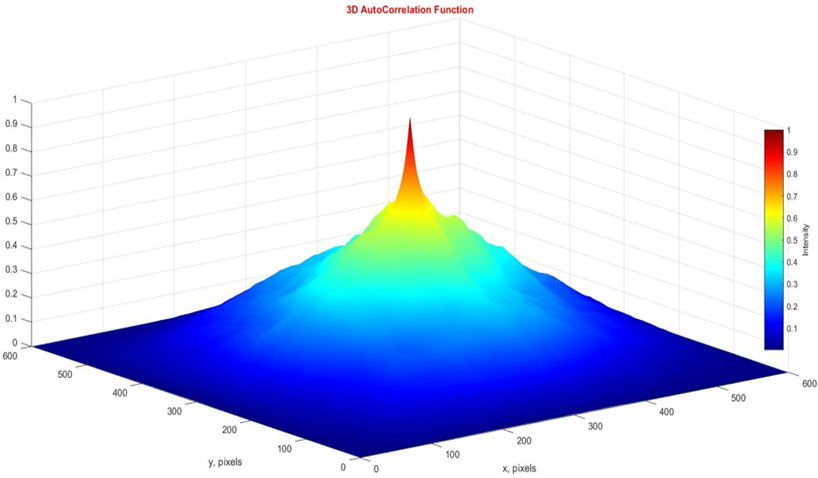
Figure 3. Two-dimensional autocorrelation function ACF(x,y) of the tomogram T(m×n) of blood sample from research group 2

Analysis the ACF(x,y) dependences of blood films birefringence distributions for both groups demonstrated a different degree of correlation coordinate coherence T(m×n). This information is indicated by a digital decrease in the eigenvalues of ACF when the value of the coordinate shifts (x,y) increases. This is most clearly manifested in the varying kurtosis values of the autocorrelation dependences ACF(x,y). It turned out to be significantly larger for coordinate optically anisotropic distributions of birefringence blood films from sick of prostate cancer.

Quantitatively (within the statistical approach (relation (1)) parameters of autocorrelation and fractal distributions of polarization tomograms illustrate the corresponding two-dimensional and one-dimensional distributions in figure 4 and figure 5.

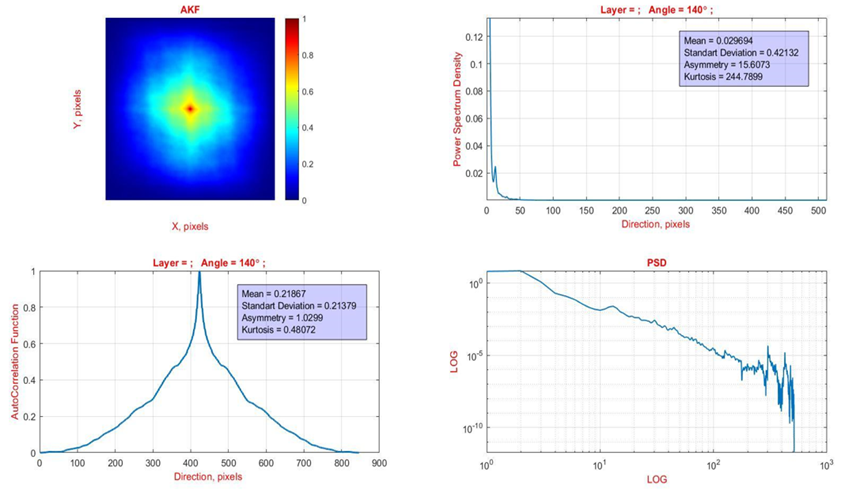
Figure 4. Correlation (left column) and fractal (right column) parameters of birefringence blood layers tomograms T(m×n) – normal

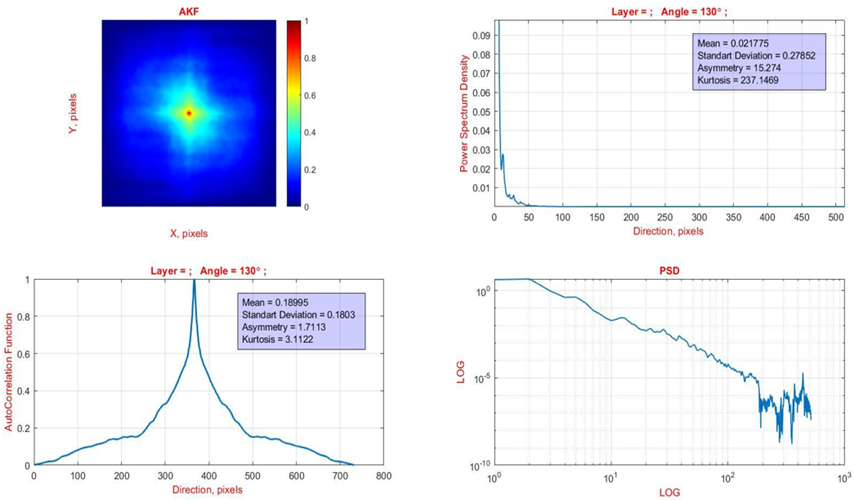
Figure 5. Correlation (left column) and fractal (right column) parameters of birefringence blood layers tomograms T(m×n) - prostate cancer

Within the framework of the correlation analysis (ratios (2),(3)), the greatest sensitivity to the pathological change in the coordinate coherence of the optically anisotropic domains of polarization tomograms T(m×n) of the asymmetry (differences up to 70 %) and excess, was established (differences up to 9 times) of distributions of eigenvalues of autocorrelation distributions.

In order to further optimize the algorithmic analysis of differential diagnosis, a fractal approach was used to analyze polarization tomograms of blood films samples optical anisotropy from both groups.

Fractal analysis

Comparison of logarithmic dependences LogSP(T(m×n))-Log(ν) of the power spectra density (PSD) of autocorrelation distributions ACF(x,y) (figure 4 and figure 5, right columns) revealed for both types of blood film samples a similar multifractal structure of tomograms T(m×n) in medium and large areas.

For small sizes of structural domains, the distributions are statistical.

Statistical analysis of distributions of autocorrelation functions PSD extremes of birefringence blood films tomograms revealed an additional parameter of their differentiation.

The maximum differences (up to 70 %) occur for the value of dispersion, which characterizes the distribution of the extreme values of the PSD.

The revealed fact of varying degrees of large-scale self-similarity of the optical anisotropy maps parameters of birefringence blood films was analyzed using wavelet transformation (relation (4),(5)).

The tomograms T(m×n) wavelet analysis data are shown in fragments of figure 6 and figure 7.

The upper row is coordinate and linear dependencies of wavelet coefficients value.

The bottom row shows the autocorrelation function of the linear distribution of wavelet coefficients obtained for scanning the MHAT function with the analytical window scale a. The second fragment is the logarithmic dependence of the power spectrum density of the autocorrelation distribution function of wavelet coefficients on a scale a.

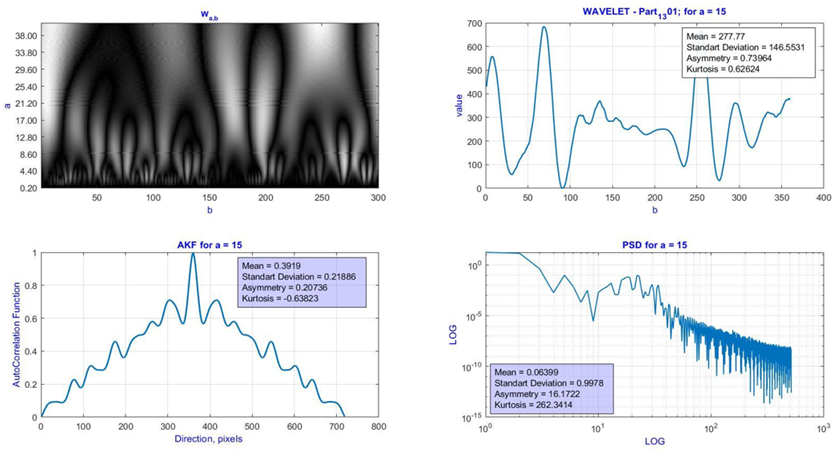
Figure 6. Results of complex correlation and fractal analysis of wavelet transform data of polarization tomograms T(m×n) of polycrystalline blood films of healthy donors

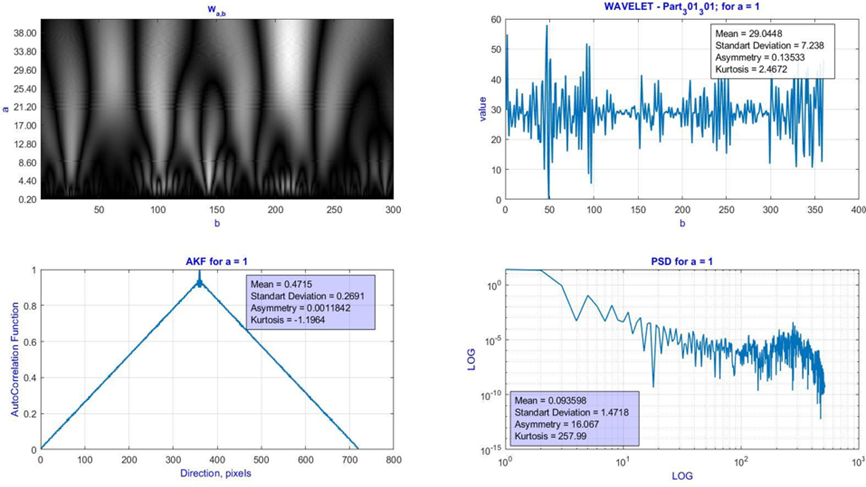
Figure 7. Results of complex correlation and fractal analysis of wavelet transform data of T(m×n) polarization tomograms of polycrystalline blood films of prostate cancer patients

Multiparametric (statistical, autocorrelation, fractal) algorithmic analysis of the tomograms T(m×n) wavelet transforms data demonstrated clear differences between both groups of blood layers – “normal - prostate cancer”.

Through algorithmic optimization, a set of new cancer detection markers was determined:

· The statistical parameters U_i=1;2;3;4, which characterize the wavelet coefficients linear distributions of optical anisotropy maps T(m×n) - the differences between these statistical markers lie in the range from 4 (asymmetry) to 20 (dispersion) times.

· The 3rd order statistical parameter (asymmetry) of the wavelet coefficients autocorrelation function of birefringence blood layers - the differences between these statistical markers lie within two orders of magnitude.

· For normal state, the wavelet coefficients distributions are multifractal.

· For prostate cancer, the distributions of the wavelet amplitude coefficients are multifractal.

Thus, a multiparameter approach to solving the problem of diagnosing prostate cancer was successfully solved using global optimization of statistical, correlation, multifractal and wavelet algorithms for intelligent data processing of an engineering biophysical system for laser tomography of dehydrated blood films.

To include: opinions, POV of the authors in this subject, debate, others authors results analysis, comparison with similar studies.

The presented results are in good agreement with the data of numerous research groups that specialize in the field of polarimetry of biological objects.^{(16,17,18,19,20,21)}

The basic principle of such studies is the concept of optical anisotropy, which is formed as a result of the growth of biological structures.

The main such structures are optically active protein molecules with chiral closed rings. These molecular complexes exhibit circular birefringence, which is optically manifested in the rotation of the plane of polarization of propagating laser radiation.

Experimentally, this effect manifests itself in the formation of coordinately distributed values of circular birefringence or tomograms of optical activity.

As a result of crystallization processes, a supramolecular network that is self-similar in configuration and optical properties is formed, which has linear birefringence.

Experimentally, the degree of this scale self-similarity is detected using fractal estimates based on the features of the logarithmic dependences of the power spectra of the distributions of optical anisotropy parameters.

Thus, the presented results of complex statistical, correlation and fractal algorithmic analysis are in accordance with known laser polarimetry data.^{(16,17,18,19,20,21)}

CONCLUSIONS

The main areas of application of artificial intelligence for algorithmic analysis and optimization of information flows in tasks of multiparametric diagnostics by means of computer engineering are considered.

A comparative analysis of the algorithmic optimization of differentiation of cancer through the use of multiparametric statistical, correlational, fractal and wavelet analysis of laser birefringence tomograms of dehydrated blood layers for control (normal) and research (cancer) groups are presented.

BIBLIOGRAPHIC REFERENCES

1. Suprunenko S, Pishenina T, Pitel N, Voronkova A, Riabovolyk T. Analysis of the Impact of Globalization Trends in the Digital Economy on Business Management and Administration Systems of Enterprises. Futur Econ Amp Law [Internet]. 2024 May 9 [cited 2024 Jul 3]:131-47. Available from: https://doi.org/10.57125/fel.2024.06.25.08.

2. Oklander M, Yashkina O, Chukurna I, Oklander T, Radkevych L, Sinkovska V. Economic and Mathematical Modeling of Innovative Development of the Agglomeration on the Basis of Information Technologies. J Inf Technol Manag [Internet]. 2023 Mar 15 [cited 2024 Jul 3]:1-13. Available from: https://doi.org/10.22059/jitm.2023.90723.

3. Storozhyk M. Philosophy of Future: Analytical Overview of Interaction Between Education, Science, and Artificial Intelligence in the Context of Contemporary Challenges. Futur Philos [Internet]. 2024 Jan 15 [cited 2024 Jul 3]:23-47. Available from: https://doi.org/10.57125/fp.2024.03.30.02.

4. Oneshko S. Assessing the Profitability of IT Companies: International Financial Reporting Standards. REF [Internet]. 2023 [cited 2024 Jul 3]; 21. Available from: https://refpress.org/ref-vol21-a149/.

5. Nykonets LO, Molnar MM, Sabat MB, Buchkovskyi IR. Modelling of Electromagnetic Processes in Transformer Windings Under the Influence of Internal Network Overvoltage. Nauk Visn Natl Hirnych Univ [Internet]. 2014 May [cited 2024 Jul 3]:58-63. Available from: https://nvngu.in.ua/index.php/en/home/991-engcat/archive/2014/contents-no-5-2014/electrical-complexes-and-systems/2790-modelling-of-electromagnetic-processes-in-transformer-windings-under-the-influence-of-internal-network-overvoltage.

6. Vladov S, Petchenko M, Shmelov Y, Drozdova S, Yakovliev R. Helicopters Turboshaft Engines Parameters Identification at Flight Modes Using Neural Networks. IEEE 17th International Conference on Computer Sciences and Information Technologies (CSIT) [Internet]. 2022 [cited 2024 Jul 3]:5-8. Available from: https://doi.org/10.1109/CSIT56902.2022.10000444.

7. Yuzevych V, Skrynkovskyy R, Koman B. Intelligent Analysis of Data Systems for Defects in Underground Gas Pipeline. 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP) [Internet]. 2018 [cited 2024 Jul 3]:134-138. Available from: https://doi.org/10.1109/DSMP.2018.8478560.

8. Hrypynska NV, Dykha MV, Korkuna NM, Tsehelyk HH. Applying Dynamic Programming Method to Solving the Problem of Optimal Allocation of Funds between Projects. Journal of Automation and Information Sciences [Internet]. 2020 [cited 2024 Jul 3];52(1):56-64. Available from: https://doi.org/10.1615/JAutomatInfScien.v52.i1.60.

9. Dorogyy Y, Tsurkan V, Mokhor V, Doroha-Ivaniuk O. Critical IT Infrastructure Resource Distribution Algorithm. Proceedings of the 11th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications, IDAACS [Internet]. 2021 [cited 2024 Jul 3];2:632-639. Available from: https://doi.org/10.1109/IDAACS53288.2021.9660948.

10. Paranchuk YS, Lysiak VH. Energy efficient power supply system and automatic control of modes of the power supply–pumping station complex. Naukovyi Visnyk Natsionalnoho Hirnychoho Universytetu [Internet]. 2018 [cited 2024 Jul 3];(3):115-124. Available from: https://doi.org/10.1109/DSMP.2018.8478560.

11. Kucherov D, Kozub A, Sushchenko O, Skrynkovskyy R. Stabilizing the spatial position of a quadrotor by the backstepping procedure. Indonesian Journal of Electrical Engineering and Computer Science [Internet]. 2021 [cited 2024 Jul 3];23:1188-1199. Available from: https://doi.org/10.11591/ijeecs.v23.i2.pp1188-1199.

12. Khan WA, Rauf A, Masud MAU, Akbar T. Relationship among Secondary School Students’ Physics Academic Achievement Scores, Conceptual Knowledge and Problem-Solving Skills. Futurity of Social Sciences [Internet]. 2024 [cited 2024 Jul 3];2(1):56-71. Available from: https://doi.org/10.57125/FS.2024.03.20.03.

13. Sopilnyk L, Dotsenko V, Aleksandraviciute B. Preservation of labour potential in the Ukrainian healthcare sector: on the way to the third SDG fulfilment in pandemic conditions. Law, Business and Sustainability Herald [Internet]. 2021 [cited 2024 Jul 3];1(3). Available from: https://doi.org/10.46489/lbsh.2021-1-3-3.

14. Ushenko VA, Hogan BT, Dubolazov A, et al. Embossed topographic depolarisation maps of biological tissues with different morphological structures. Sci Rep [Internet]. 2021 Feb 16 [cited 2024 Jul 3];11(1):3871. Available from: https://doi.org/10.1038/s41598-021-83017-2.

15. Ushenko A, Dubolazov A, Zheng J, Bakun O, Gorsky M, Ushenko Y. Mueller matrix polarization interferometry of optically anisotropic architectonics of biological tissue object fields: the fundamental and applied aspects. Frontiers in Physics [Internet]. 2022 [cited 2024 Jul 3];11:1302254. Available from: https://doi.org/10.3389/fphy.2023.1302254.

16. Sdobnov A, Ushenko VA, Trifonyuk L, Bakun O, et al. Mueller-matrix imaging polarimetry elevated by wavelet decomposition and polarization-singular processing for analysis of specific cancerous tissue pathology. Journal of Biomedical Optics [Internet]. 2023 [cited 2024 Jul 3];28(10):102903-102903. Available from: https://doi.org/10.1117/1.JBO.28.10.102903.

17. Ushenko A, Zheng J, Gorsky M, Dubolazov A, Ushenko Y, et al. 3D digital holographic polarimetry of diffuse optically anisotropic biological tissue object fields. Frontiers in Physics [Internet]. 2023 [cited 2024 Jul 3];11:1288935. Available from: https://doi.org/10.3389/fphy.2023.1288935.

18. Ushenko A, Zheng J, Litvinenko A, Gorsky M, Wanchuliak O, Dubolazov A, Ushenko Y, Soltys I, Salega O, Chen Z. 3D digital polarization-holographic wavelet histology in determining the duration of mechanical damage to the myocardium. J Biophotonics [Internet]. 2024 Mar [cited 2024 Jul 3];17(3). Available from: https://doi.org/10.1002/jbio.202300372.

19. Ushenko A, Dubolazov A, Zheng J, Litvinenko A, Gorsky M, Ushenko Y, et al. 3D polarization-interference holographic histology for wavelet-based differentiation of the polycrystalline component of biological tissues with different necrotic states. Journal of Biomedical Optics [Internet]. 2024 [cited 2024 Jul 3];29(5):052920-052920. Available from: https://doi.org/10.1117/1.JBO.29.5.052920.

20. Ushenko YA, Koval GD, Ushenko AG, Dubolazov OV, Ushenko VA, et al. Mueller-matrix of laser-induced autofluorescence of polycrystalline films of dried peritoneal fluid in diagnostics of endometriosis. Journal of Biomedical Optics [Internet]. 2016 [cited 2024 Jul 3];21(7):071116-071116. Available from: https://doi.org/10.1117/1.JBO.21.7.071116.

21. Angelsky PO, Ushenko AG, Dubolazov AV, et al. The singular approach for processing polarization-inhomogeneous laser images of blood plasma layers. Journal of Optics [Internet]. 2013 [cited 2024 Jul 3];15(4):044030. Available from: http://iopscience.iop.org/2040-8986/15/4/044030.

FINANCING

No financing.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest.

AUTHORSHIP CONTRIBUTION

Conceptualization: Volodymyr Yakhno, Vadym Kolumbet.

Data curation: Petar Halachev.

Formal analysis: Ruslan Ivanenko, Petar Halachev.

Research: Vadym Kolumbet, Ruslan Ivanenko.

Project management: Vadym Kolumbet.

Resources: Vladyslav Khambir, Ruslan Ivanenko.

Software: Vladyslav Khambir.

Supervision: Volodymyr Yakhno.

Validation: Petar Halachev, Ruslan Ivanenko.

Visualization: Vladyslav Khambir.

Drafting - original draft: Vadym Kolumbet, Ruslan Ivanenko.

Writing - proofreading and editing: Volodymyr Yakhno, Petar Halachev.