doi: 10.56294/dm2024319
ORIGINAL
Prediction of extreme weather using nonparametric regression approach with Fourier series estimators
Predicción de fenómenos meteorológicos extremos mediante un enfoque de regresión no paramétrica con estimadores de series de Fourier
Ihsan Fathoni Amri1,4 ![]() *, Nur Chamidah2,3
*, Nur Chamidah2,3 ![]() *, Toha Saifudin2,3
*, Toha Saifudin2,3 ![]() *, Dannu Purwanto4
*, Dannu Purwanto4 ![]() *, Alwan Fadlurohman4
*, Alwan Fadlurohman4 ![]() *, Ariska Fitriyana Ningrum4
*, Ariska Fitriyana Ningrum4 ![]() *, Saeful Amri4
*, Saeful Amri4 ![]() *
*
1Airlangga University, Doctoral Study Program of Mathematics and Natural Sciences, Faculty of Science and Technology. Surabaya, Indonesia.
2Airlangga University, Departement of Mathematics, Faculty of Science and Technology. Surabaya, Indonesia.
3Airlangga University, Research Group of Statistical Modeling in Life Science, Faculty of Science and Technology. Surabaya, Indonesia.
4University Muhammadiyah Semarang, Department of Data Science. Semarang, Indonesia.
Cite as: Fathoni Amri I, Chamidah N, Saifudin T, Purwanto D, Fadlurohman A, Fitriyana Ningrum A, Amri S. Prediction of extreme weather using nonparametric regression approach with Fourier series estimators. Data and Metadata. 2024; 4:319. https://doi.org/10.56294/dm2024319
Submitted: 27-01-2024 Revised: 01-04-2024 Accepted: 29-06-2024 Published: 30-06-2024
Editor: Adrián
Alejandro Vitón Castillo ![]()
ABSTRACT
In Jepara, Central Java, Indonesia, significant correlations between high rainfall and wind speed impact multiple sectors including health, agriculture, and infrastructure. This study aims to predict the effects of extreme weather by employing nonparametric regression based on Fourier series estimators. Data from December 2023 to March 2024, sourced from NASA, were analyzed using sinus, cosinus, and combined Fourier functions to model the dynamic and seasonal fluctuations of weather variables. This approach allows for a flexible modeling of these previously undefined functional relationships. The analysis revealed that the combined function model was superior, achieving an optimal Generalized Cross-Validation (GCV) score of 0,236498 with a Fourier coefficient K=3, indicating a well-fitted model. Moreover, this model exhibited a low Mean Absolute Percentage Error (MAPE) of 1,887, demonstrating high predictive accuracy. These findings not only affirm the efficacy of Fourier series in nonparametric regression for weather forecasting but also underscore its potential in informing public policy and bolstering disaster preparedness in Jepara and similar regions vulnerable to extreme weather conditions.
Keywords: Nonparametric Regression; Fourier Series; Extreme Weather; Rainfall; Wind Speed; Predictive Accuracy; Generalized Cross-Validation (GCV); Mean Absolute Percentage Error (MAPE).
RESUMEN
En Jepara, Java Central (Indonesia), las correlaciones significativas entre las altas precipitaciones y la velocidad del viento afectan a múltiples sectores, como la sanidad, la agricultura y las infraestructuras. Este estudio pretende predecir los efectos del clima extremo empleando una regresión no paramétrica basada en estimadores de series de Fourier. Los datos de diciembre de 2023 a marzo de 2024, procedentes de la NASA, se analizaron utilizando funciones senoidales, cosenoidales y combinadas de Fourier para modelizar las fluctuaciones dinámicas y estacionales de las variables meteorológicas. Este enfoque permite un modelado flexible de estas relaciones funcionales previamente indefinidas. El análisis reveló que el modelo de función combinada era superior, alcanzando una puntuación óptima de validación cruzada generalizada (GCV) de 0,236498 con un coeficiente de Fourier K=3, lo que indica un modelo bien ajustado. Además, este modelo mostró un bajo porcentaje medio de error absoluto (MAPE) de 1,887, lo que demuestra una elevada precisión predictiva. Estos resultados no sólo afirman la eficacia de las series de Fourier en la regresión no paramétrica para la predicción meteorológica, sino que también subrayan su potencial para informar las políticas
públicas y reforzar la preparación ante desastres en Jepara y regiones similares vulnerables a condiciones meteorológicas extremas.
Palabras clave: Regresión no Paramétrica; Series de Fourier; Condiciones Meteorológicas Extremas; Precipitaciones; Velocidad del Viento; Precisión Predictiva; Validación Cruzada Generalizada (GCV); Error Porcentual Absoluto Medio (MAPE).
INTRODUCTION
In recent years, the occurrence of natural phenomena due to extreme weather has become one of the main focuses of study, especially in the climatology study section. The occurrence of global climate change resulting in changes in weather patterns is the main cause of increased frequency and intensity of rainfall in several regions in Indonesia.(1) Heavy rainfall often damages existing infrastructure, such as roads, bridges, and drainage systems, causing disruptions in the transportation sector and logistics distribution.(2) In addition to physical damage, high rainfall can also cause flooding, trigger landslides, cause various diseases, and damage natural habitats.(3)
In agricultural areas, extreme rainfall damages crops, which in turn affects agricultural productivity and further causes food price fluctuations.(4) In the social sector, high rainfall disrupts the economic cycle by forcing business and production activities to stop temporarily.(5) Then in the education sector high rainfall often leads to school closures.(6) The impact on the social sector is the potential for increased social isolation for individuals in affected communities, especially the elderly or those with limited mobility.(7)
Therefore, it is necessary to conduct this research related to rainfall and influencing factors. So as to reduce the impact of high rainfall. The knowledge gained can guide public policies and strategies aimed at minimizing negative impacts and increasing community resilience to the challenges presented by extreme weather.
In this study, rainfall was selected as the response variable Y and wind speed as the predictor variable X. An analysis in statistics used to investigate the pattern of functional relationships between the response variable Y and the predictor variable X is called regression analysis.(8) In regression analysis to estimate the pattern of functional relationships between response variables and predictor variables, two approaches are used, namely parametric regression and nonparametric regression approaches.(9) If the functional relationship between the response and predictor variables is assumed to follow a certain curve pattern, including linear, quadratic, cubic, and exponential, a parametric approach is suitable and if the shape of the functional relationship pattern is unknown, a nonparametric regression approach is used.(10) The nonparametric regression approach basically has high flexibility because the regression function is assumed to be smooth and not specified to have a certain shape so that in its estimation it can use certain smoothing methods by looking at the data pattern. There are several smoothing techniques that can be used in nonparametric regression approaches, including kernel estimators, linear local estimators, local polynomial estimators, spline estimators, Fourier series and so on.(11)
Regression analysis using a parametric regression approach and also nonparametric regression has been carried out by several researchers. Parametric regression research on cross section data that has been carried out by several researchers is quartile regression and high-dimensional regression.(12,13) Research on nonparametric regression analysis on cross section data was conducted on spline estimator, on kernel estimator, on linear local estimator and on Fourier series estimator.(14,15,16,17) Research using a parametric approach to time series data including conducted(18) combined Markov switching model and volatility model, linear regression studied, Autoregressive Integreted Moving Average (ARIMA) model studied and ARIMAX.(19,20,21) While research with a nonparametric approach to time series data includes kernel estimators conducted, linear local estimators, spline estimators, Fourier series estimators and local polynomial estimators.(22,23,24,25,26,27)
In regression analysis, several optimization methods include methods such as Least Squares (LS), Penalized Least Squared (PLS), Weigthed Least Squares (WLS) and many others. Some of the research that has been done includes(28) examining nonparametrics using LS(17) examining nonparametrics using the Fourier series and PLS(29) conducting research on Fourier series estimators in semiparametric regression using WLS optimization. PLS is an optimization method that provides a smoothing component to the LS method with optimization criteria that combine data fit with curve smoothness. PLS estimation is done to balance data adjustment and avoid excessive roughness.(30) Basically, PLS is very good to use because according Chen C et al.(31) states that in general Generalized Cross Validation (GCV) cannot choose parameters that are really good because the overfitting effect is ignored in the resulting model.(32) Researching on Penalized Maximum Likelihood Estimation (PMLE) states a suitable method to overcome overfitting, which means that PLS can also be used to avoid overfitting.
Research on the Fourier series estimator in semiparametric regression based on PLS has never been done either in terms of theory or in terms of application. The Fourier series estimator is one of the estimators in the nonparametric regression model that is able to overcome the fluctuating data pattern that rises high or falls far around a certain value. In rainfall data, which is very large and contains seasonal elements, it causes fluctuations around a high value and at a certain time then decreases to a much lower value, therefore it is suitable for use in the Fourier series estimator. The repeating pattern of data is very suitable for the Fourier series estimator, in the form of repetition of different independent variables.(33) Air pressure is a very important climate controller on earth, because of its role as a determinant in the distribution of rainfall in various regions on earth. Large rainfall will cause a lot of water on the surface to overflow so that the river cannot fully drain the water discharge and eventually cause flooding.(34) Rainfall is the amount of rain discharge that occurs and is recorded directly in an area which is observed by the rainfall observation station every day.(35) Ernyasih E et al.(36) stated in his research that the amount of rainfall had an impact on the health sector, not only on the health sector(37) also stated that the agricultural sector was also affected by changes in rainfall in Indonesia.(38) argues that Jepara is one of the areas that since January 2019 has been adversely affected quite a lot in several sectors such as health and agriculture due to the very high rainfall discharge compared to other days. Therefore, it is necessary to study rainfall as a variable and the factors that influence it in Jepara. One of the factors that affect rainfall is wind speed which is used as a predictor variable.
In Jepara, Central Java, the observation of rainfall and wind speed data reveals periodic patterns over time, highlighting the need for a dynamic and adaptable modeling approach. The scatter plots between rainfall and wind speed indicate that the functional relationship between these variables is not readily discernible. This unpredictability necessitates the use of a nonparametric regression model with Fourier series estimators, specifically chosen to address the unknown functional relationships and the fluctuating patterns observed between these weather variables. The primary objective of this research is to develop a robust model capable of effectively predicting the impacts of these weather variables on the local environment. By employing the nonparametric regression approach, this study leverages the flexibility of the Fourier series to capture the inherent variability in the data. This method enhances the accuracy and reliability of the weather predictions, which are crucial for effective disaster preparedness in Jepara.
METHOD
Study Design and Data Collection
This study utilized a nonparametric regression approach with Fourier series estimators to analyze the relationship between rainfall and wind speed in Jepara, Central Java. Data for this analysis was collected from December 2023 to March 2024, sourced from NASA and validated with additional data from the Meteorology, Climatology, and Geophysics Agency (BMKG) of Indonesia.
Research Variables
The response variable used in this study is daily rainfall data in Jepara. The predictor variables used are factors that affect rainfall, one of which is wind speed. The variables used are described in table 1.
|
Table 1. Variables Structure |
||
|
Notation |
Variable |
Detail |
|
yt |
Rainfall |
The rainfall amount on a given day |
|
gt |
Wind Speed |
Wind speed on a given day |
|
T |
Time |
Number of daily observations over a given period |
Modeling Approach
The primary modeling technique involved the use of Fourier series estimators to address the non-linear and periodic nature of the data. These estimators were particularly chosen for their ability to model unknown functional relationships and handle fluctuating patterns between rainfall and wind speed. The Fourier series model incorporated sinusoidal and cosinus functions to effectively capture the dynamics of the weather patterns.
Regression analysis is an analysis that is used to determine the pattern of functional relationships between response and predictor variables. One approach where the pattern of the relationship between the response variable and the predictor is unknown is nonparametric. Given a nonparametric regression model:(39,40,41,42,43)
![]()
Where y is response variable, g(.) is unknown smooth function and Et is zero mean and σ2 variance random error. To unknown smooth function in equation 1, we use Fourier series estimator. In this study g(Vt) which is approximated by the following Fourier series function. The sinus function on Fourier series given by exponential complex function:
![]()
Where γ, α0, b is parameter in nonparametric function. The cosinus function on Fourier series given by exponential complex function:
![]()
Where γ, α0, a is parameter in nonparametric function. Then the sinus and cosinus on Fourier series given by exponential complex function:
![]()
Where γ, α0, a, b is parameter in nonparametric function.
Optimization and Validation
To get the best estimation, one of the most important things is to choose an optimal bandwidth with associated Fourier series function. This can be done using Generalized Cross-Validation criterion with formula 5:
![]()
Statistical Analysis
For the step of statistical analysis is:
1. Data Collection
· Data on rainfall and wind speed were gathered from December 2023 to March 2024.
· The primary sources of data were NASA and the Meteorology, Climatology, and Geophysics Agency (BMKG) of Indonesia, ensuring comprehensive coverage and validation.
2. Initial Data Assessment
· Preliminary analysis involved plotting scatter plots of rainfall against wind speed to visually inspect the data for any obvious patterns or relationships.
3. Model Selection
· Nonparametric regression with Fourier series estimators was selected as the modeling approach due to the non-linear and periodic nature of the weather data.
· The Fourier series model utilized sinusoidal and cosinus functions to capture the complex dynamics of the weather patterns.
4. Function Implementation
· The Fourier series were applied using separate sinus, cosinus, and combined functions to model the relationship between rainfall and wind speed.
· Each model variant was implemented to evaluate its effectiveness in capturing the underlying patterns in the data.
5. Optimization Process
· Generalized Cross-Validation (GCV) was used to optimize the model by selecting the best Fourier coefficient (K-value). This process involves minimizing the GCV score to find the most suitable model that fits the data well without overfitting.
6. Model Evaluation
· The Mean Absolute Percentage Error (MAPE) was calculated for each model configuration to measure its predictive accuracy.
· The models were compared based on their MAPE values, with lower values indicating higher accuracy and better performance.
7. Final Model Selection
· The model configuration yielding the lowest MAPE and GCV scores was selected as the optimal model for predicting the relationship between rainfall and wind speed.
8. Prediction Implementation
· The selected model was then used to make predictions about future weather patterns based on the relationship identified between rainfall and wind speed.
· Predictions were validated against additional data sets to assess the model's reliability and accuracy in real-world conditions.
9. Result Analysis and Reporting
· The outcomes of the predictive model were analyzed to understand the impact of extreme weather on the local environment in Jepara.
· Significant findings were documented and prepared for reporting in the study's results section, highlighting the effectiveness of the chosen statistical techniques in weather prediction.
Results Interpretation
The final step involved interpreting the results based on the established criteria, with specific attention to MAPE value, to determine the most accurate and reliable model for predicting the impact of extreme weather on the local environment in Jepara. The MAPE for looking the best model is:
![]()
Where T is the size of the sample, ŷt is the value predicted by the model for time point t and y is the value observed at time point t. The criteria for MAPE values are shown in the following table 2.
|
Table 2. MAPE Value Criteria |
|
|
MAPE |
Definition |
|
< 10 |
Highly Accurate |
|
10 – 20 |
Accurate |
|
20 – 50 |
Reasonable |
|
>50 |
Inaccurate |
RESULTS
In this section, discuss the results of the analysis on rainfall and wind speed in Jepara Indonesia. The data obtained in the form of time series data from December 2023 to March 2024 comes from NASA and is validated with data from BMKG Indonesia. For initial justification, namely checking the correlation of rainfall with wind speed. The following are the results of the correlation between rainfall and wind speed:

Figure 1. Confusion Matrix between rainfall and wind speed
It can be seen in figure 1 that the image is close to the red and blue colors, meaning that there is a correlation between rainfall and wind speed. So based on the justification, an analysis will be carried out to determine the functional relationship between rainfall and wind speed using a nonparametric regression approach. The first step is to look at the scatter plot to provide an assumption that the functional relationship does not form a certain curve pattern. The following is the scatter plot between rainfall and wind speed:
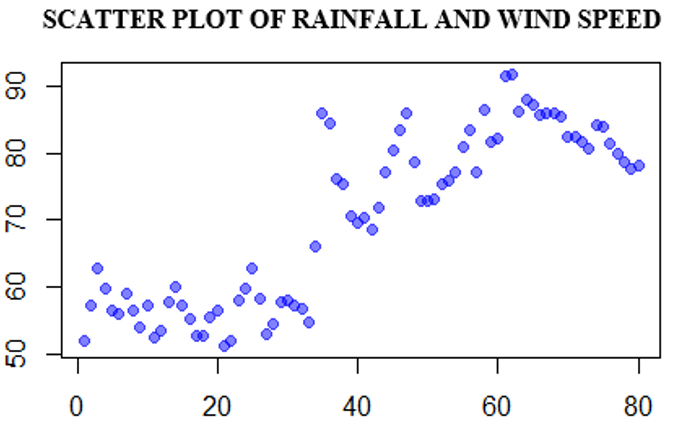
Figure 2. Scatter Plot of Rainfall and Wind Speed
Based on the figure above, it can be seen that the scatter plot does not form a certain pattern. However, to strengthen this, linear, quadratic and cubic tests were conducted. The following are the results of parameter significance in each test:
|
Table 3. Linear, quadratic and cubic tests |
|
|
|
p-value |
|
LM |
<2e-16 |
|
KD |
<2e-16 |
|
KB |
<2e-16 |
The results in table 3. Strengthen the assumption that the scatter plot does not form a specific curve because the value of p-value in each test is more than a=0,05.
If it is proven that the scatter plot does not form a certain pattern, a nonparametric regression analysis using the Fourier series estimator is performed. The first stage in nonparametric regression using the Fourier series estimator is to determine the minimum GCV value on each lambda. The change in lambda value is used to overcome overfitting. Then it is applied to each Fourier coefficient which in this case we set as many as 10. The following are the results of the selection of the minimum GCV on the sinus, cosinus, and combined functions:
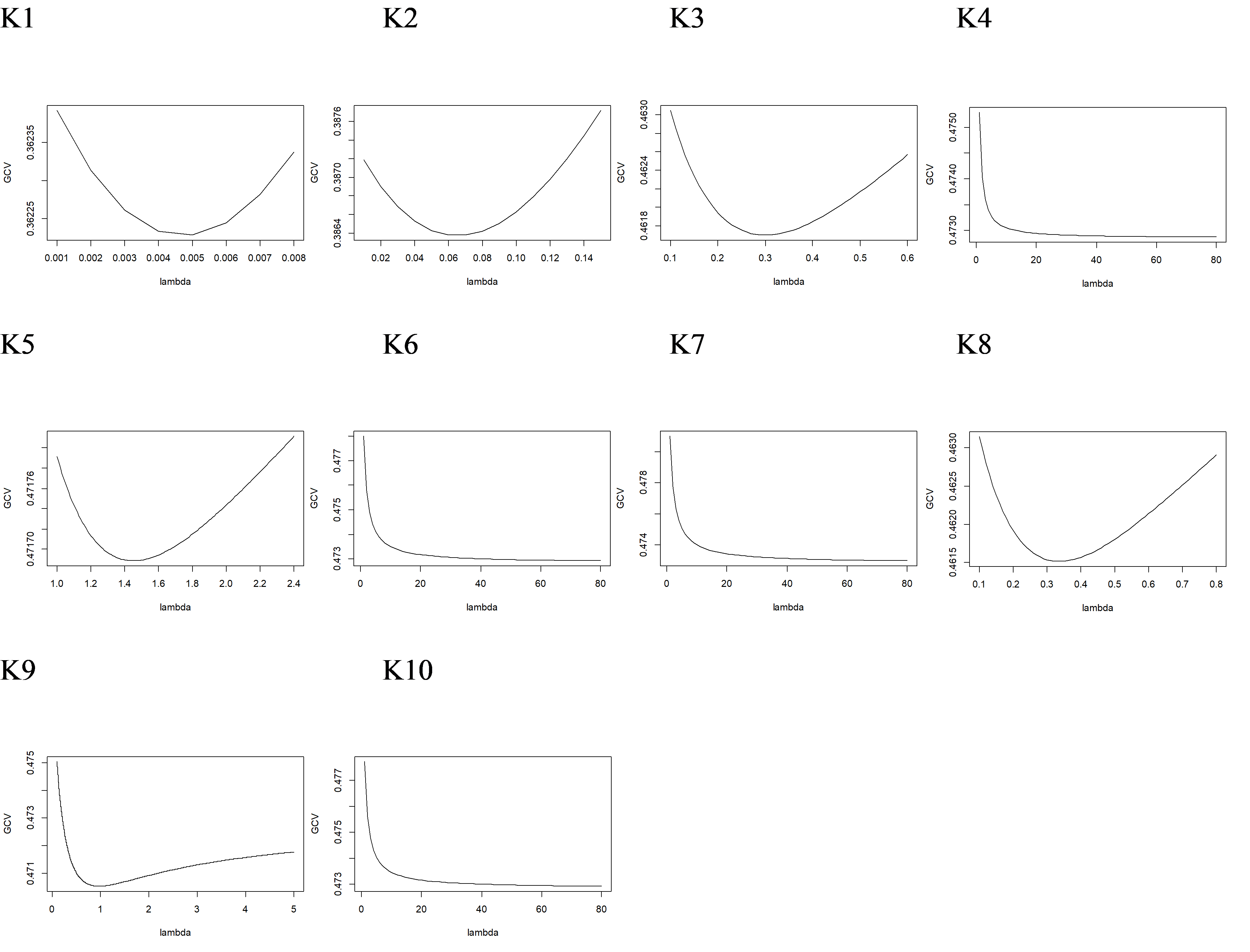
Figure 3. GCV Plot of Sinus Function
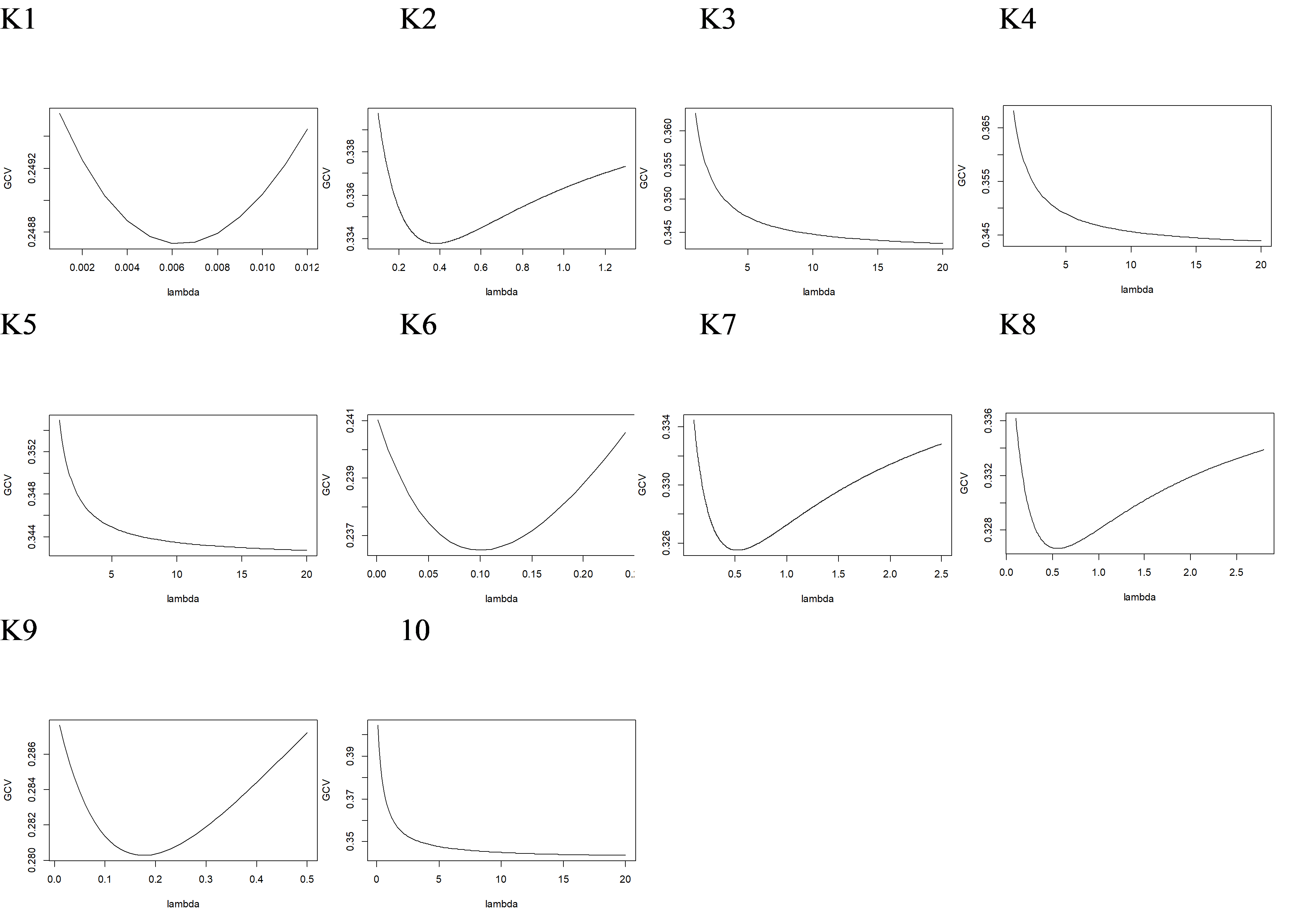
Figure 4. GCV Plot of Cosinus Function
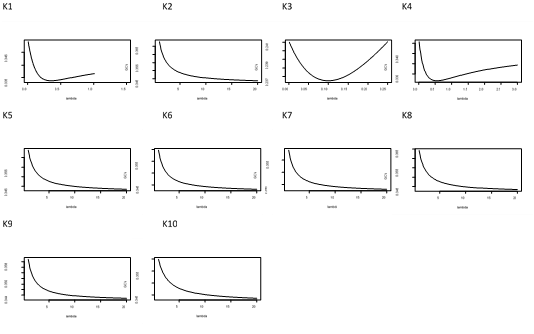
Figure 5. GCV Plot of Sinus and Cosinus Functions
Based on the GCV plot of figure 3 to figure 5, it can be seen that each function has a minimum GCV value. The minimum value of each function is presented in the following table:
|
Table 4. Minimum GCV and Lambda Values for Each Fourier Coefficient |
||||||||
|
Function |
Sinus |
|
Cosinus |
|
Sinus and Cosinus |
|||
|
K |
GCV |
Lambda |
K |
GCV |
Lambda |
K |
GCV |
Lambda |
|
1 |
0,4658771 |
99 |
1 |
0,3863733 |
0,0614 |
1 |
0,3337836 |
0,36 |
|
2 |
0,4639826 |
0,24 |
2 |
0,4728689 |
79 |
2 |
0,3438216 |
19 |
|
3 |
0,4294802 |
0,04 |
3 |
0,4729293 |
79 |
3 |
0,236498 |
0,1 |
|
4 |
0,3746454 |
0,016 |
4 |
0,4730912 |
-79 |
4 |
0,3266246 |
0,55 |
|
5 |
0,3728737 |
0,03 |
5 |
0,4729232 |
79 |
5 |
0,3435036 |
19 |
|
6 |
0,3906429 |
0,05 |
6 |
0,4730797 |
-79 |
6 |
0,3432016 |
19 |
|
7 |
0,4194249 |
0,09 |
7 |
0,4733741 |
-79 |
7 |
0,3431409 |
19 |
|
8 |
0,4587442 |
0,35 |
8 |
0,4739249 |
-79 |
8 |
0,3435949 |
19 |
|
9 |
0,4659256 |
99 |
9 |
0,4729318 |
-79 |
9 |
0,3429616 |
19 |
|
10 |
0,4610382 |
0,53 |
10 |
0,4728395 |
-79 |
10 |
0,3437124 |
19 |
In table 4, the GCV value of sinus has a greater average than cosinus and the combination of the two. While for GCV cosinus is greater than the GCV of the two functions combined. The following table compares the Optimal K value, Minimum GCV, and Lmabda of each function:
|
Table 5. Comparison of K, GCV, and Lambda Values for Each Function |
|||
|
|
Sinus |
Cosinus |
Sinus and Cosinus |
|
K |
5 |
1 |
3 |
|
GCV |
0,3728737 |
0,3863733 |
0,236498 |
|
Lambda |
0,03 |
0,0614 |
0,01 |
Based on Table 5, it can be concluded that knowing the best value in nonparametric using the Fourier series can be seen from the GCV. It can be seen that the minimum GCV value is in the combination of the two functions and is at Fourier coefficient 3 with a GCV value of 0,236498 and lambda 0,1. So that the sinus and cosinus models that can be formed are:
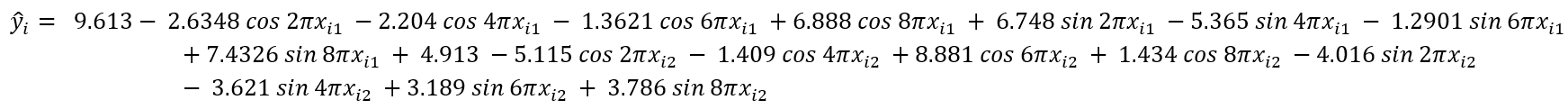
Because the ultimate goal of this research is prediction, it is also necessary to look at the criteria for model goodness. For the criteria of model goodness used in this study, namely MAPE, so each function is seen by the MAPE value. The following are the results of MAPE on each function:
|
Table 6. Comparison of MAPE Values for Each Function |
|||
|
|
Sinus |
Cosinus |
Sinus dan Cosinus |
|
MAPE |
5,761 |
2,917 |
1,887 |
It can be seen in table 6. that the smallest MAPE value is also obtained in the combination of both sinus and cosinus functions. In the table it can also be read that the sinus, cosinus, and combined functions are quite well used for prediction. It's just that to get the best results in prediction, the combined function of the two can be used.
|
Table 7. Rainfall Prediction Using Combined Functions |
||
|
Prediction Combined Functions |
||
|
Time |
Rainfall Prediction |
Rainfall Data |
|
10 March 2024 |
6,29 |
7,99 |
|
11 March 2024 |
15,64 |
12,31 |
|
12 March 2024 |
4,13 |
5,78 |
|
13 March 2024 |
3,46 |
4,08 |
|
14 March 2024 |
7 |
7,52 |
|
15 March 2024 |
6,48 |
7,37 |
|
16 March 2024 |
13,18 |
11,93 |
|
17 March 2024 |
7,14 |
8,01 |
|
18 March 2024 |
11,69 |
10,68 |
|
19 March 2024 |
7,54 |
8,07 |

Figure 6. Comparison plot of actual and predicted rainfall data
Based on table 7 and figure 6, it can be seen that the value of rainfall search does not have significant fluctuations. Only it cannot be used for justification in reading the prediction results because it requires expert exposure also in the field of weather to read the value of the prediction results in detail. However, it can be used as a reference in determining policies because it is not much different from the original data.
DISCUSSION
Our analysis of extreme weather patterns in Jepara, Central Java, Indonesia, using nonparametric regression approaches and Fourier series estimators reveals significant correlations between high rainfall and wind speed, impacting multiple sectors including health, agriculture, and infrastructure. hal itu diperkuat dalam research conducted(36) which states that rainfall affects the agricultural sector which is also affected by changes in rainfall in Indonesia. These findings are crucial as they diverge from traditional models that often do not capture the non-linear and seasonal variations inherent in seasonal data.
In contrast to parametric models, which assume a predefined relationship between variables, our approach adapts to the inherent irregularities of environmental data. This flexibility is exemplified in the superior performance of the combined sinus and cosinus Fourier series model, which not only provided the lowest Generalized Cross-Validation (GCV) score but also demonstrated high predictive accuracy with a low Mean Absolute Percentage Error (MAPE).
These results underline the efficacy of Fourier series in capturing complex, dynamic patterns in weather data, which are often missed by simpler linear or polynomial models. This is particularly relevant given the increasing unpredictability of weather patterns due to climate change, as noted in recent studies(28,29). Furthermore, the successful application of this method provides a robust framework for improving disaster preparedness and informing public policy in regions vulnerable to extreme weather conditions.
Despite these promising outcomes, our study is not without limitations. The reliance on historical data from specific datasets (NASA and BMKG) may not fully represent future conditions, especially as climate patterns continue to evolve. Additionally, the complexity of Fourier series models may limit their practical application by local meteorological agencies without specialized training.
Future research should focus on integrating more diverse data sources, including real-time satellite imagery and ground reports, to enhance the model's responsiveness to immediate weather changes. Further exploration of machine learning techniques could also be employed to refine the accuracy of predictions and handle larger datasets more efficiently, thus supporting more timely and effective responses to extreme weather threats.
CONCLUSIONS
This study uses a nonparametric regression approach with a Fourier series estimator to explore the relationship between rainfall and wind speed. Through analysis, it was found that the combination of sinus and cosinus functions gave the most accurate prediction results. The minimum GCV value achieved was 0,236498 at Fourier coefficient K=3, indicating a good model fit to the data. In terms of prediction accuracy, the lowest MAPE value was 1,887, which was also obtained from the combination of sinus and cosinus functions, indicating a high level of accuracy in rainfall prediction. This conclusion suggests that the Fourier series approach in nonparametric regression is very useful for weather prediction models, especially in the context of extreme weather that impacts various sectors of life.
BIBLIOGRAPHIC REFERENCES
1. Samidjo J, Suharso Y. Memahami pemanasan global dan perubahan iklim. Online Journal of Ivet University. 2017;24(2):36–46.
2. Syukur A. Buku Pintar Penanggulangan Banjir. DIVA PRESS; 2021.
3. Hermon D. Geografi bencana alam. PT. RajaGrafindo Persada-Rajawali Pers; 2015.
4. Hidayat A. DAMPAK PERUBAHAN IKLIM TERHADAP PERTANIAN DAN STRATEGI ADAPTASI YANG DITERAPKAN OLEH PETANI. 2023;
5. Tumpu M, Jamal M, SYAHRIR M, Pasanda OSR, Lapian FEP, Rustam MSPA, et al. Infrastruktur berbasis mitigasi bencana. TOHAR MEDIA; 2023.
6. Laksmi GS. Dampak Alih Fungsi Lahan dan Curah Hujan terhadap Banjir di Kota Pekalongan, Jawa Tengah. In: Seminar Nasional Lahan Suboptimal. 2020. p. 382–91.
7. Susilawati S. Dampak perubahan iklim terhadap kesehatan. Electronic Journal Scientific of Environmental Health And Disease. 2021;2(1):25–31.
8. Anandari AA. Analisis Regresi Deret Fourier: Aplikasi Data Curah Hujan. CV Jejak (Jejak Publisher); 2023.
9. Hidayat R, Yuliani Y, Sam M. Model regresi nonparametrik dengan pendekatan spline truncated. Prosiding. 2018;3(1).
10. Khairunnisa LR, Prahutama A, Santoso R. PEMODELAN REGRESI SEMIPARAMETRIK DENGAN PENDEKATAN DERET FOURIER (Studi Kasus: Pengaruh Indeks Dow Jones dan BI Rate Terhadap Indeks Harga Saham Gabungan. Jurnal Gaussian. 2020;9(1):50–63.
11. Utami TW, Prahutama A, Karim A, Achmad ARF. Modelling rice production in Central Java using semiparametric regression of local polynomial kernel approach. In: Journal of Physics: Conference Series. IOP Publishing; 2019. p. 012108.
12. Mösching A, Dümbgen L. Monotone least squares and isotonic quantiles. 2020;
13. Azriel D, Schwartzman A. Estimation of linear projections of non-sparse coefficients in high-dimensional regression. 2020;
14. Al Azies H, Hapsery A. Spline Nonparametric Regression Approach For Modeling Factors Affecting Vocational National Exam Results in Surabaya. Vol. 1, PROCEEDINGS OF THE 1 st STEEEM. 2019. 244–252 p.
15. Rodriguez-Poo JM, Soberón A. Nonparametric estimation of fixed effects panel data varying coefficient models. J Multivar Anal. 2015;133:95–122.
16. Chamidah N, Rifada M. Estimation of median growth curves for children up two years old based on biresponse local linear estimator. In: AIP Conference Proceedings. AIP Publishing; 2016.
17. Saputro DRS, Sukmayanti A, Widyaningsih P. The nonparametric regression model using Fourier series approximation and penalized least squares (PLS)(case on data proverty in East Java). In: Journal of Physics: Conference Series. IOP Publishing; 2019. p. 012019.
18. Amri IF, Chamidah N. Early detection models of currency crises in Indonesia based on inflation and interest rates indicators. In: Journal of Physics: Conference Series. IOP Publishing; 2020. p. 012018.
19. Yolanda Y. Analysis of factors affecting inflation and its impact on human development index and poverty in Indonesia. 2017;
20. Sari V. Model Hybrid ARIMA dan Neural Network untuk Meramalkan Data Time Series. Majalah Ilmiah Median. 2016;9(1).
21. Ahmad IS, Setiawan S, Suhartono S, Masun NH. Forecasting of monthly inflow and outflow currency using time series regression and ARIMAX: The Idul Fitri effect. In: AIP Conference Proceedings. AIP Publishing; 2015.
22. Sahoo D, Hoi SCH, Li B. Large scale online multiple kernel regression with application to time-series prediction. ACM Transactions on Knowledge Discovery from Data (TKDD). 2019;13(1):1–33.
23. Aydın D, Ahmed SE, Yılmaz E. Right-Censored Time Series Modeling by Modified Semi-Parametric A-Spline Estimator. Entropy. 2021;23(12):1586.
24. Lee T, Ouarda TBMJ, Yoon S. KNN-based local linear regression for the analysis and simulation of low flow extremes under climatic influence. Clim Dyn. 2017;49:3493–511.
25. Prahutama A, Utami TW. Modelling Fourier regression for time series data-a case study: modelling inflation in foods sector in Indonesia. In: Journal of Physics: Conference Series. IOP Publishing; 2018. p. 012067.
26. Chamidah N, Febriana SD, Ariyanto RA, Sahawaly R. Fourier series estimator for predicting international market price of white sugar. In: AIP Conference Proceedings. AIP Publishing; 2021.
27. Chamidah N, Lestari B. Estimation of covariance matrix using multi-response local polynomial estimator for designing children growth charts: A theoretically discussion. In: Journal of Physics: Conference Series. IOP Publishing; 2019. p. 012072.
28. Asrini LJ, Budiantara N. FOURIER SERIES SEMIPARAMETRIC REGRESSION MODELS (CASE STUDY: THE PRODUCTION OF LOWLAND RICE IRRIGATION IN CENTRAL JAVA). 2014;9(9). Available from: www.arpnjournals.com
29. Kuzairi, Chamidah N, Budiantara IN. Theoretical Study of Fourier Series Estimator in Semiparametric Regression for Longitudinal Data Based on Weighted Least Square Optimization. In: Proceedings of the 1st International Multidisciplinary Conference on Education, Technology, and Engineering (IMCETE 2019) [Internet]. Atlantis Press; 2020. p. 264–7. Available from: https://doi.org/10.2991/assehr.k.200303.064
30. Varet S, Lacour C, Massart P, Rivoirard V. Numerical performance of penalized comparison to overfitting for multivariate kernel density estimation. ESAIM: Probability and Statistics. 2023;27:621–67.
31. Chen C, Ren M, Zhang M, Zhang D. A two-stage penalized least squares method for constructing large systems of structural equations. Journal of Machine Learning Research. 2018;19(2):1–34.
32. Bai J, Liao Y. Efficient estimation of approximate factor models via penalized maximum likelihood. J Econom. 2016;191(1):1–18.
33. Salim MI, Sauddin A, Nawawi MI. Model Regresi Nonparametrik Deret Fourier Pada Kasus Tingkat Pengangguran Terbuka Di Sulawesi Selatan. Jurnal MSA (Matematika dan Statistika serta Aplikasinya). 2022;10(2):48–56.
34. Pradipta NS, Sembiring P, Bangun P. ANALISIS PENGARUH CURAH HUJAN DI KOTA MEDAN. Vol. 1. 2013.
35. Susilowati S, Sadad I. Analisa karakteristik curah hujan di Kota Bandar Lampung. Konstruksia. 2015;7(1).
36. Ernyasih E, Fajrini F, Latifah N. Analisis Hubungan Iklim (Curah Hujan, Kelembaban, Suhu Udara dan Kecepatan Angin) dengan Kasus ISPA di DKI Jakarta Tahun 2011–2015. Jurnal Ilmu Kesehatan Masyarakat. 2018;7(3):167–73.
37. Sumastuti E, Pradono NS. Dampak perubahan iklim pada tanaman padi di Jawa Tengah. Journal of Economic Education. 2016;5(1):31–8.
38. Sholekhah NW, Nugraha AL, Awwaluddin M. ANALISIS ANCAMAN TERHADAP BENCANA BANJIR DAN TANAH LONGSOR PADA WILAYAH PERMUKIMAN DI KABUPATEN JEPARA. Jurnal Geodesi Undip. 2021;10(2):29–35.
39. Chamidah N, Lestari B, Budiantara IN, Aydin D. Estimation of Multiresponse Multipredictor Nonparametric Regression Model Using Mixed Estimator. Symmetry (Basel) [Internet]. 2024 Mar 25;16(4):386. Available from: https://www.mdpi.com/2073-8994/16/4/386
40. Gao J, Hawthorne K. Semiparametric estimation and testing of the trend of temperature series. Econom J [Internet]. 2006 Jul 1;9(2):332–55. Available from: https://doi.org/10.1111/j.1368-423X.2006.00188.x
41. Sahidah S, Kuzairi K, Mardianto MFF. Estimator Deret Fourier Dalam Regresi Nonparametrik Dengan Penalti Untuk Perencanaan Penjualan Produk Musiman. Zeta - Math Journal. 2022 Nov 25;7(2):69–78.
42. Green PJ, Silverman BW. Nonparametric regression and generalized linear models: a roughness penalty approach. Crc Press; 1993.
43. Montaño J, Palmer A, Sesé A, Cajal B. Using the R-MAPE index as a resistant measure of forecast accuracy. Psicothema. 2013 Nov 1;25:500–6.
FINANCING
This research was funded through the Junior Lecturer Research program, which is an internal fund from Universitas Muhammadiyah Semarang. The fund is intended to support the development of early research by lecturers who are just starting their academic careers, enabling the collection and analysis of rainfall and wind speed data in Jepara, Indonesia from December 2023 to March 2024.
CONFLICT OF INTEREST
The authors declare that no conflict of interest is associated with this research. The research process was conducted objectively and independently, without influence from any stakeholder that could benefit personally or institutionally.
AUTHORSHIP CONTRIBUTION
Conceptualization: Ihsan Fathoni Amri, Nur Chamidah.
Data curation: Ihsan Fathoni Amri.
Formal analysis: Ariska Fitriyana Ningrum.
Acquisition of funds: Ihsan Fathoni Amri, Nur Chamidah.
Research: Ihsan Fathoni Amri.
Methodology: Ihsan Fathoni Amri, Toha Saifudin.
Project management: Saeful Amri.
Resources: Dannu Purwanto.
Software: Saeful Amri.
Supervision: Ariska Fitriyana Ningrum, Nur Chamidah.
Validation: Dannu Purwanto, Toha Saifudin.
Display: Alwan Fadlurohman.
Drafting - original draft: Ihsan Fathoni Amri.
Writing - proofreading and editing: Alwan Fadlurohman, Nur Chamidah.