doi: 10.56294/dm2024262
ORIGINAL
Hybrid Feature Selection with Chaotic Rat Swarm Optimization-Based Convolutional Neural Network for Heart Disease Prediction from Imbalanced Datasets
Selección de funciones híbridas con red neuronal convolucional basada en optimización de enjambre de ratas caóticas para la predicción de enfermedades cardíacas a partir de conjuntos de datos desequilibrados
Sasirega. D1 *, Dr.Krishnapriya.V2 *
1Ph.D Scholar, Sri Ramakrishna College of Arts and Science, Assistant Professor KG college of Arts and Science. Coimbatore, Tamil Nadu-641006, India.
2Associate Professor and Head, Department of Computer Science and Cognitive Systems, Sri Ramakrishna College of Arts and Science. Coimbatore, Tamil Nadu-641006, India.
Cite as: Sasirega D, Krishapriya V. Hybrid Feature Selection with Chaotic Rat Swarm Optimization-Based Convolutional Neural Network for Heart Disease Prediction from Imbalanced Datasets. Data and Metadata. 2024; 3:262. https://doi.org/10.56294/dm2024262
Submitted: 20-11-2023 Revised: 02-03-2024 Accepted: 16-05-2024 Published: 17-05-2024
Editor: Adrián
Alejandro Vitón Castillo ![]()
ABSTRACT
Introduction: early diagnosis of Cardiovascular Disease (CVD) is vital in reducing mortality rates. Artificial intelligence and machine learning algorithms have increased the CVD prediction capability of clinical decision support systems. However, the shallow feature learning in machine learning and incompetent feature selection methods still pose a greater challenge. Consequently, deep learning algorithms are needed to improvise the CVD prediction frameworks.
Methods: this paper proposes an advanced CDSS for CVD detection using a hybrid DL method. Initially, the Improved Hierarchical Density-based Spatial Clustering of Applications with Noise (IHDBSCAN), Adaptive Class Median-based Missing Value Imputation (ACMMVI) and Clustering Using Representatives-Adaptive Synthetic Sampling (CURE-ADASYN) approaches are introduced in the pre-processing stage for enhancing the input quality by solving the problems of outliers, missing values and class imbalance, respectively. Then, the features are extracted, and optimal feature subsets are selected using the hybrid model of Information gain with Improved Owl Optimization algorithm (IG-IOOA), where OOA is improved by enhancing the search functions of the local search process. These selected features are fed to the proposed Chaotic Rat Swarm Optimization-based Convolutional Neural Networks (CRSO-CNN) classifier model for detecting heart disease.
Results: four UCI datasets are used to validate the proposed framework, and the results showed that the OOA-DLSO-ELM-based approach provides better heart disease prediction with high accuracy of 97,57 %, 97,32 %, 96,254 % and 97,37 % for the four datasets.
Conclusions: therefore, this proposed CRSO-CNN model improves the heart disease classification with reduced time complexity for all four UCI datasets.
Keywords: Cardiovascular Diseases; Adaptive Synthetic Sampling; Improved Owl Optimization Algorithm; Chaotic Rat Swarm Optimization; Convolutional Neural Networks.
RESUMEN
Introducción: el diagnóstico precoz de las Enfermedades Cardiovasculares (ECV) es vital para reducir las tasas de mortalidad. Los algoritmos de inteligencia artificial y aprendizaje automático han aumentado la capacidad de predicción de ECV de los sistemas de apoyo a las decisiones clínicas. Sin embargo, el aprendizaje de características superficial en el aprendizaje automático y los métodos de selección de características incompetentes aún plantean un desafío mayor. En consecuencia, se necesitan algoritmos de aprendizaje profundo para improvisar los marcos de predicción de CVD.
Métodos: este artículo propone un CDSS avanzado para la detección de ECV utilizando un método DL híbrido. Inicialmente, en el preprocesamiento se introducen los enfoques de agrupación espacial de aplicaciones con ruido basada en densidad jerárquica mejorada (IHDBSCAN), imputación de valor perdido basada en la mediana de clase adaptativa (ACMMVI) y agrupación mediante muestreo sintético adaptativo de representantes (CURE-ADASYN). etapa para mejorar la calidad de la entrada resolviendo los problemas de valores atípicos, valores faltantes y desequilibrio de clases, respectivamente. Luego, se extraen las características y se seleccionan los subconjuntos de características óptimos utilizando el modelo híbrido de ganancia de información con el algoritmo de optimización Owl mejorado (IG-IOOA), donde la OOA se mejora mejorando las funciones de búsqueda del proceso de búsqueda local.Estas características seleccionadas se alimentan al modelo clasificador de redes neuronales convolucionales basado en la optimización de enjambres de ratas caóticas (CRSO-CNN) propuesto para detectar enfermedades cardíacas.
Resultados: se utilizan cuatro conjuntos de datos UCI para validar el marco propuesto, y los resultados mostraron que el enfoque basado en OOA-DLSO-ELM proporciona una mejor predicción de enfermedades cardíacas con una alta precisión de 97,57 %, 97,32 %, 96,254 % y 97,37 % para los cuatro conjuntos de datos.
Conclusiones: Por lo tanto, este modelo CRSO-CNN propuesto mejora la clasificación de enfermedades cardíacas con una complejidad temporal reducida para los cuatro conjuntos de datos de la UCI.
Palabras clave: Enfermedades Cardiovasculares; Muestreo Sintético Adaptativo; Algoritmo de Optimización de Búhos Mejorado; Optimización de Enjambre de Ratas Caóticas, Redes Neuronales Convolucionales.
INTRODUCTION
Cardiovascular disease (CVDs) is a range of diseases that affect the heart and blood vessels that perform important activities in the human body. Globally, around 20,5 million deaths are reported due to CVDs by the World Health Organization (WHO) and are considered a global health problem. The symptoms of heart disease are irregular heartbeats, tightness in the chest, nausea, breathing disability, discomfort in arms and legs, fainting, weakness, and chest pain.(1) The heart and blood vessels are affected due to cholesterol blocks or narrowing of veins that cause the inability to pump blood to other organs. This leads to sudden heart dysfunction and the prevalence of the mortality risk. Some potential risk factors associated with CVDs are smoking, stress, alcohol consumption, high blood pressure, being inactive, unhealthy diets and obesity. These risk factors are considered as modifiable risk factors. Some non-modifiable risk factors causing heart disease are family history, age, gender and ethnicity. Thus, early prediction is essential to reduce death rates and improve the quality of life. Various diagnostics techniques and treatments are available to identify and minimize the risk of CVDs. These include blood tests, echocardiograms, stress tests, electrocardiograms, chest X-rays, and cardiac catheterization(2) and medications such as adenosine, atropine, beta-blockers, calcium, potassium and sodium channel blockers and digoxin are prescribed-based on the type and severity of the disease.(3) However, these methods are costly and require more time for diagnostics. Early and timely prediction with improved risk assessments and accurate diagnosis can minimize the death rate. Thus, Clinical decision support systems (CDSS) are introduced to increase the screening of CVD risk factors and help diagnose CVD-related diseases through preventive care services, clinical tests, and treatments.(4)
CDSS are computer-based systems that aid the process of diagnostics, disease prediction, and clinical management, reduce the risk of clinical errors, monitor patients’ response to the treatment and improve patient outcomes. The traditional statistical methods that work with the principle of identifying the correlation and association between the data patterns of patients were employed. Generally, CDSS uses regression analysis, survival analysis such as Kaplan-Meier curves and Cox proportional hazards models, and hypothesis testing like t-tests and chi-squared tests to determine the significance of associations in clinical data.(5) Bayesian statistical methods were also employed in CDSS to incorporate prior knowledge, update probabilities, and support diagnostic or predictive tasks. Data mining methods are employed to analyze historical data and identify the associations in data patterns using techniques such as clustering, association rules discovery, regression, sequential patterns discovery, and collaborative filtering.(6) However, data mining techniques include potential bias in the data and struggle with complex or unstructured data sets that require additional pre-processing steps. Machine learning (ML) methods were used to overcome these challenges by automating the process of data analysis and pattern recognition. ML models can parse data, learn from them, and then apply the knowledge gained to make intelligent predictions. ML can handle complex and unstructured data sets more efficiently and helps identify hidden patterns and trends in data that were not identified using traditional statistical methods.(7) ML algorithms play a crucial role in CDSS by analyzing patient data to provide useful information and aid medical decision-making. However, the ML algorithm is always based on shallow learning of features in data that could not gather significant heart disease information. To overcome these challenges, deep learning (DL) techniques are utilized for heart disease classification. DL methods can provide accurate classification results that help medical practitioners conclude the presence and absence of heart disease. However, DL algorithms are considered black boxes as it is difficult to interpret and explain the reason behind predictions. This is because DL models have multiple layers and require more time to learn the features.(8) Despite these challenges, DL has gained popularity due to its ability to automatically learn and extract complex patterns from patient data compared to ML models. Hence, lightweight DL models are developed for CVD prediction to reduce the standard DL model's challenges significantly.
Considering the advantages and challenges in heart disease prediction, an intelligent CDSS framework for CVD prediction using an advanced deep learning method is proposed. The proposed model comprises three stages: pre-processing, feature extraction and selection, and classification. In the pre-processing stage, the acquired datasets are pre-processed to detect and remove outliers, imputing the missing values and balancing the dataset to overcome class imbalance problems. The proposed model utilizes an IHDBSCAN method for detecting and removing outliers. The HDBSCAN method(9) is limited to handling clusters of varying densities and poses high computational complexity when data points are huge. Thus, the initial clusters of HDBSCAN are uniquely redefined in IHDBSCAN to reduce the complexity and slow processing for similar density clusters for outlier removal. After removing the outliers, the missing value imputation is performed using the proposed ACMMVI method. The ACMMVI method replaces the missing values based on the attribute type with the class median values. The threshold values are calculated based on the distances between the class median and the other observed data points. Then, the class imbalance problem in the dataset is resolved using the CURE-ADASYN method. The standard ADASYN(10) faced the difficulty of handling datasets for generating new instances to balance the number of samples and increase the computational complexity of the minority class. CURE reduces the computational complexity of ADASYN by improving the initial clustering of balanced classes. This helps to represent the majority and minority class data better, leading to a more accurate classification by balancing the data. In the second stage, feature extraction and selection are applied.
The proposed feature selection method combines the Information gain (IG)-based filter method and the Improved Owl Optimization (IOOA)-based wrapper method to form a hybrid IG-IOOA algorithm, where the IOOA selects the optimal feature subsets based on IG. IOOA is developed by improving the search functions of the local search process of OOA. The method of selecting optimal feature subsets can lead to faster model training. Finally, the selected features are fed as input to the classifier model, CRSO-CNN, for heart disease classification. The RSO is improved by integrating the chaotic process to enhance its exploration capabilities and improve its convergence speed, and then it is used to optimally select the hyper-parameters of the CNN classifier to form the best configured CNN model. This best-configured CNN can efficiently reduce the training time and improve the training process. The CRSO-CNN model can contribute to more accurate and efficient heart disease diagnosis and risk assessment. The proposed CRSO-CNN model was evaluated using UCI Datasets- Cleveland, Hungary, Switzerland and VA Long Beach and the method provides high accuracy and low complexity in predicting heart disease.
Previously, Asadi et al.(11) proposed a method of multi-objective particle swarm optimization (MOPSO) and a Random Forest (RF) for predicting heart disease. Evaluations are performed using Statlog, Cleveland, SPECT, SPECTF, and VA Long Beach datasets and obtained 88,26 %, 87,65 %, 86,70 %, 87,50 %, and 80,95 % respectively. However, because of the high number of iterations, these model approaches consume excess time to generate training sets for training decision trees. Mehmood et al.(12) presented a deep learning method of Convolutional Neural Networks (CNN)-based Cardio Help model for predicting cardiovascular disease. Evaluations are performed using Cleveland datasets and obtained 97 % prediction accuracy. However, this method has high computational complexity. Mienye et al.(13) proposed a method of PSO technique and stacked sparse autoencoder (SSAE) for predicting heart disease. Evaluations are performed using Framingham and Cleveland datasets and obtained the classification accuracy of 0,973 and 0,961, respectively. However, PSO's performance is sensitive to the values of its parameters, such as the acceleration coefficients and population size. Sekar et al.(14) proposed a Tuned Adaptive Neuro-Fuzzy Interference System (TANFIS) for heart disease prediction. Evaluations are performed using Kaggle datasets and obtained a classification accuracy of 99,86 %. However, this method consumes more time. Budholiya et al.(15) proposed a method of optimized Extreme Gradient Boost (XGBoost) classifier to predict heart disease. Evaluations are performed using the Cleveland dataset, and the model achieves accuracy, sensitivity, specificity, F1-score, and AUC of 91,8 %, 96,9 %, 85,7 %, 90,5 %, and 92,8 %, respectively. Although this model reduces the complexity, the feature learning capability is limited.
Al Bataineh et al.(16) proposed a multilayer perceptron particle swarm optimization algorithm (MLP-PSO) method to diagnose heart disease. Evaluations are performed using the Cleveland dataset, and the model achieves an accuracy of 84,61 %. PSO is robust in controlling parameters, easy to implement, and computationally efficient. However, the PSO takes more time (22,6) for convergence to find a solution. El-Shafiey et al.(17) combined genetic algorithm (GA), particle swarm optimization (PSO) and Random Forests (GAPSO-RF) for heart disease detection. It achieved high accuracies of 87,8 % (10-fold) and 95,6 % (holdout) for the Cleveland and 87,78 % (10-fold) and 91,4 % (holdout) for the Statlog datasets. However, computational cost and temporal complexity are high due to wrapper-based selection in GAPSO. Paul et al.(18) introduced a scaled conjugate gradient back propagation method of artificial neural networks using K-fold cross-validation for predicting heart disease. Evaluations are performed using the Cleveland processed dataset and the Cleveland Hungarian Statlog heart dataset and obtained an accuracy of 63,38 % and 88,47 %, respectively. However, in this method, the Cleveland processed dataset takes more time (54,2264 seconds) and provides less accuracy. Shrivastava et al.(19) combined CNN and Bidirectional Long Short-Term Memory (Bi-LSTM) to predict heart disease. Evaluations are performed using the Cleveland dataset, and the model achieves accuracy, precision, recall, and f1-score values of 96,66 %, 96,84 %, 96,66 %, and 96,63 %, respectively. However, this method faced computational latency and model complexity. Yaqoob et al.(20) proposed a modified artificial bee colony optimization method with a support vector machine (MABC-SVM) to diagnose heart disease. Evaluations are performed using the Kaggle dataset, and the model achieves an accuracy of 93,8 % and reduces classification error by 1,6 %. However, it can be challenging to interpret this model's predictions and understand the importance of individual features, especially with complex kernels.
Elsedimy et al. (21) introduced a method by combining a quantum-behaved particle swarm optimization (QPSO) algorithm and a support vector machine (SVM) for predicting cardiovascular disease. Evaluations were performed using the Cleveland dataset and obtained 96,31 % prediction accuracy. However, SVMs have model complexity due to increased support vectors for learning the features. Almazroi et al.(22) proposed a Clinical Decision Support System (CDSS) using a Keras-based-dense neural network (DNN) to diagnose heart disease. Evaluations are performed using Cleveland, Hungarian, Long Beach, and Switzerland datasets and obtained accuracies of 82,49 %, 81,02 %, 60,06 %, and 64 %, respectively. However, this model was poorly performed for the Switzerland and Long Beach datasets, with only 60 % accuracy achieved because it failed to handle the NaN values in the datasets. The existing methods showed that many ML and DL algorithms have been used for predicting heart diseases. Common challenges include computational latency, high computational costs, time consumption, and complexity. To overcome these limitations, the proposed method uses a lightweight CDSS using effective pre-processing methods, IG-IOOA for feature selection and CRSO-CNN classifier for predicting heart disease from imbalanced datasets.
METHODS
|
Table 1. List of variables used in this study |
|
|
〖dist〗_core |
Core distance |
|
minPts |
Nearest neighbour among a minimum neighbours |
|
〖 d(x〗_p,〖 x〗_q) |
Normal Euclidean distances |
|
ES (C_i) |
Stability of the cluster |
|
D_(_complete) |
Complete data |
|
D_(_incomplete), |
Instances with missing values |
|
cent(D_i ) |
Euclidean distances between the class centre |
|
|
Distance between the instance and |
|
dist(y_i,x_2) |
A minority and majority class samples |
|
〖 l〗_mi and〖 l〗_ma |
Total number of synthetic data |
|
G |
Parameter that specifies the desired balance level |
|
β |
The distance between the two clusters |
|
dist (S,T) |
The distance between the two data items (p, q) |
|
dist(p,q) |
The centre point of the clusters |
|
S_r and〖 S〗_c |
An instance ratio (number of majority neighbours/number of minority neighbours). |
|
r_i |
The number of synthetic data samples |
|
g_i |
Probability distribution of the samples |
|
Re and ▁Re |
The probability distribution |
|
p |
Binary function represents the logarithmic value, for the events X and Y |
|
H(Y) and H(Y|X) |
The clustering process and nest renewal |
|
〖PP〗_(num,) 〖SP〗_(num,) and〖 Dep〗_(nest,) |
Random values |
|
R_(1,) and〖 R〗_(2,) |
The number of primary branches |
|
〖PP〗_(num,) |
The number of Owls |
|
〖OW〗_(n,) |
The number of secondary perches |
|
〖SP〗_num |
New positions |
|
〖 OW〗_new |
The population of rats is initialized in this CRSO |
|
P ⃗_i |
The position of the rat in the i-th iteration |
|
P ⃗_best |
The position of the optimal rat |
|
B and r |
Random numbers |
|
P ⃗_(i+1) |
The position of the next rat |
The proposed method for heart disease prediction involves three stages: Data pre-processing, Feature extraction and selection and classification. The pre-processing stage is improved by imputing the missing data and removing the outliers and class imbalance problems. To enhance these problems, suitable methods like IHDBSCAN, ACMMVI and CURE-ADASYN methods are introduced. The features are extracted and selected in the next stage. The feature selection is performed using a hybrid model of the IG-IOOA algorithm. The final classification stage is performed using the proposed CRSO-CNN model. The total work method of this suggested approach is shown in figure 1.
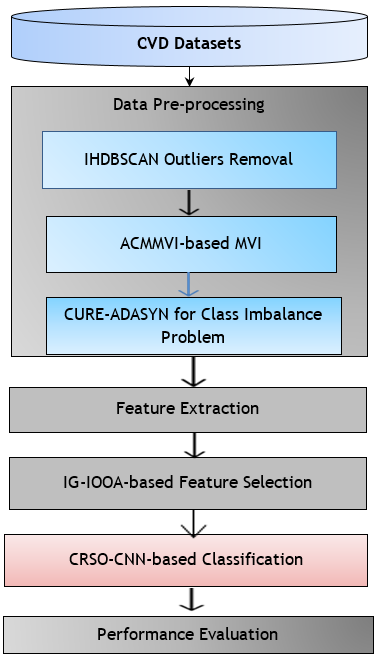
Figure 1. Workflow of Proposed Methodology
Data pre-processing
The CVD datasets contain outlier removal, missing value impute, and class imbalance problems. These problems can degrade the input information's effectiveness and decrease the evaluation's effectiveness. Therefore, using suitable methods, the datasets are pre-processed to enhance the data quality and representation. In this pre-processing step, removing the outliers, imputing missing values, and balancing class are vital tasks to improve the data quality. As stated earlier, the three methods of IHDBSCAN, ACMMVI, and CURE-ADASYN are utilized for these purposes in the pre-processing section.
Outlier Removal using Improved Hierarchical DBSCAN
In this proposed approach, an Improved Hierarchical DBSCAN technique is implemented to remove outliers. This technique is developed from the HDBSCAN method because it handles datasets with irregularly shaped clusters, varying cluster densities, and noisy data. Declining as an outlier method is done to remove small clusters using the HDBSCAN cluster selection process. In this process, cluster selection does not depend upon the global epsilon threshold, but it creates an effective hierarchy for all the epsilon values for minPts a minimum cluster size. The first step is to find mutual reachability distance, represented as the core distance (〖 dist〗_core) between an object and its nearest neighbor among a minimum of minPts neighbors. The two objects are represented as,〖 x〗_p and〖 x〗_q are calculated as follows:
![]()
Where, 〖 d(x〗_p,〖 x〗_q) refers to normal Euclidean distances. This method distinguishes sparse data points from the rest by ensuring they are separated by a minimum distance equal to their core distance. Therefore, the dataset can be visualized as a graph, which is used for creating a spanning tree. Next, creating a condensed cluster hierarchy method and stability-based cluster selection typically involves selecting a subset of the most significant clusters from the original hierarchy tree and the context of clustering analysis.
Finally, the Framework for Optimal Selection of Clusters (FOSC) is an approach that aims to guide the process of determining the optimal number of clusters in a clustering analysis. This measure needs to have two specific properties: local and additive. In local, the calculation for one cluster should not interfere with the calculation for another cluster. The measure should be meaningful in additive property to add up the computed cluster values. FOSC formulates the cluster selection as an optimization problem. To solve the optimization problem, FOSC uses a bottom-up approach. It's essential to ensure that exactly one cluster is selected on each branch of the hierarchical clustering tree. This requirement adds structure to the clustering solution, ensuring that clusters are well-defined and non-overlapping. FOSC is described as providing an efficient way of finding the globally optimal solution for cluster extraction based on the chosen stability measure. By efficiently traversing the hierarchy tree and making decisions at each level, FOSC aims to find the best cluster set that maximizes the sum of cluster stabilities.
However, HDBSCAN has some limitations, like taking more processing time due to its model complexity and slow processing for similar-density clusters. The IHDBSCAN technique was introduced in this proposed method with reduced computational complexity to overcome these limitations. This improved method introduces a threshold for better performance of cluster splits. Here, a threshold distance ( ε) ̂ is used for selecting a cluster from HDBSCAN.
Here, an HDBSCAN hierarchy is used as a selection method according to FOSC. The proposed method of Improved HDBSCAN using cluster selection uses epsilon stable and epsilon stability conception. A cluster is represented as C_i with the i value of {2,…,k} is called epsilon stable if ε_max (C_i )>( ε) ̂ for a given( ε) ̂>0. Whenever C_i appears, the density level is λ_min (C_i )=1/(ε_max (C_i ) ) . This is equal to its parent cluster split off. If the parent clusters split off at a distance above our threshold ( ε) ̂, then the cluster is called epsilon stable. Next, the epsilon stability is defined as:
![]()
Where ES is the stability of the cluster, the λ value is 0,2. For ( ε) ̂ and minPts, selected clusters reach the highest epsilon stability in each path of the hierarchy tree and will not further split up. The parent clusters are split up at the distance〖 ε〗_min>( ε) ̂, which is equal to the ε_max value on the level where their children appear. The child clusters are not allowed to split themselves because they are leaf clusters, or they are split when the threshold level is〖 λ〗_max=1/ε_min.
From this stability definition, problems are solved using maximizing the sum of epsilon stabilities. Also, the definition explains when exploring the hierarchy of clusters from the bottom to the top, the biggest and most cohesive clusters at each step are found, as the smaller or less significant clusters are removed. This approach helps to focus on the most substantial clusters as they move up the hierarchy, which can be useful in various data analysis and clustering tasks. The outlier removal is explained in algorithm 1:
Algorithm 1: Improved Hierarchical DBSCAN
1. Initializing δ (.) = 1 for all leaf nodes.
2. Perform a bottom-up traversal starting from all leaves, excluding the root node:
If ES(C_i) is greater than 0; if S(C_i) is 0, proceed to the next leaf node.
Else, if ES (C_i )equals 0, and the ES (C_(PARENT (i))) is greater than 0, do the following:
-Set δ_(PARENT(i)) is equal to 1,
-Set δ (.) is equal to 0 for all nodes within the sub-tree of C_(PARENT (i)).
From the above algorithm 1, start marking all the leaves in the HDBSCAN cluster hierarchy as selected. If a leaf was previously marked as not being a cluster or if it's already epsilon stable (λ_min<=1/( ε) ̂ for input parameter( ε) ̂), move on to the next leaf without any further action. Otherwise, it moves upwards in the hierarchy until it finds an ascendant that splits off from its parent at a certain density level (λ_min<=1/( ε) ̂ ). It is stopped if such an ascendant finds before encountering any of its descendants. This process guarantees that the largest epsilon stable cluster is selected along each path in the hierarchy. To move up the tree, ES (C_i) generally decreases (except for cases with 0 values). This approach guarantees the selection of the largest epsilon-stable cluster along each path. Essentially, the initial clusters choose the path that originated at a distance greater than ( ε) ̂ and, therefore, is not permitted to split.
Conceive an example cluster tree using a small sample dataset with these algorithm concepts. On the left side, the tree is marked with λ_min values, while on the right, the same tree is annotated with epsilon stability values for a parameter value of ( ε) ̂ = 5 meters, equivalent to λ=1/( ε) ̂ =0,2. Any cluster at a level that doesn't meet the epsilon stability criterion is assigned a value of 0. Conversely, clusters meeting the criterion receive λ_min as their epsilon stability value. Checking the λ_min observe that levels with values of 0,6, 0,3, and 1,4 surpass the 0,2 threshold. This implies that clusters at these levels are separated from their parent clusters at distances less than 5 meters. To obtain the final set of clusters, follow a process starting from the leaf nodes and selecting the ascendant with the highest epsilon stability value along each path. This process successfully removes outliers in this proposed approach.
Adaptive Class Median-based Missing Value Imputation
The missing value imputation is done using the ACMMVI method in this proposed method. Imputing missing values helps maintain the integrity and completeness of the data. In this ACMMVI method, missing values are replaced by the mean/mode of the data samples, which depends on the attribute type in a particular class. Threshold identification is calculated, and missing values are imputed in this method. Missing rate defined below:
![]()
The threshold identification process is based on the distances between the class centres and their correspondences to the complete data. This process begins with an incomplete dataset, denoted as D, which comprises N different classes. Divide this dataset into two subsets: D_(_complete), which contain complete data, and D_(_incomplete), which contain instances with missing values. Next, focus on each class individually within the (D_(_complete) ), subset. For a given class i D_(_incomplete) calculated the following statistics: Computed the class center for each attribute within class I, using the mean value as the class center if an attribute is numerical. For categorical attributes, designate the mode as the class center. Then, Calculated the Euclidean distances between the class center (cent(D_i )) and every data sample within Class i. This step involves measuring the difference between each instance and the class center for the specific class.
The threshold value (T1) for class i was determined based on the computed distances. Using the mean or mode for calculating distances depends on the data type. For numerical datasets, use the mean of distances. For categorical datasets, use the mode of distances. Calculate distances using the mean and mode for mixed datasets containing both numerical and categorical attributes. Then, use the mean or mode of these distances as the threshold (T1) for Class i. Repeat the above steps for each class in the dataset. This ensures a distinct threshold value for each class, considering the nature of the data within that class.
After finding threshold values, the focus is on imputed missing values, which is done in two ways based on the standard deviation (STD) of the data. If STD is less than or equal to 1, outlier detection involves calculating the distance between the imputed value and the class center. If this distance exceeds a predefined threshold, the imputed value is considered an outlier and is replaced with the median value of the attribute in that class. If STD exceeds 1, the missing value is considered an outlier. To replace it, the average weighted distance is computed according to equation (2),-based on the distances between the missing value and its nearest neighbors in the complete data.
![]()
Where W_i represents the weight distance of the ith outlier data point, y_i represents the ith instance of outlier data, and x1 represents the first instance of complete data. The function dist(y_i,x_2) is used to calculate the distance between the instance y_( i)and〖 x〗_j. This step is repeated until each instance's average weight distance is obtained. The resulting average weighted distance is then used to replace the missing value.
Class imbalance problem using CURE-ADASYN: This proposed work uses CURE-ADASYN to solve the class imbalance problem. ADASYN is one of the methods that are used for solving class imbalance problems efficiently. This algorithm adaptively generates synthetic samples for minority class instances that are difficult to classify, emphasizing those closer to the decision boundary. However, using the ADASYN method to solve the class imbalance problem faced the difficulty of handling datasets for generating new instances to balance the number of samples. Therefore, this proposed work combines the CURE algorithm and the ADASYN method for solving class imbalance problems. CURE helps to generate artificial samples randomly between representative points and the center point and cluster the sample of the minor class.
In this process, identifying the minority and majority classes is important for recognizing the impact of class imbalance. The training dataset of this process is represented as 〖TR〗_d those containing l samples {x_i,y_i }. The value of i=1,…,l , x_i is an instance, and 〖 y〗_i is the class identity label, and〖 y〗_i∈Y={1,-1} that is associated with an 〖 x〗_i instance in the n-dimensional feature space X. A minority and majority class samples are represented as 〖 l〗_mi and〖 l〗_ma. So, the value of 〖 l〗_mi ≤〖 l〗_ma and〖 l〗_mi +〖 l〗_ma=l. First, a class imbalance degree is calculated as:
![]()
Where d belongs to [0, 1] based on the class imbalance degree, the number of synthetic data samples needed for the minority class. The class imbalance degree notifies decisions related to data pre-processing. For example, if the d value is less than or equal to the present threshold 〖 d〗_th for the maximum tolerated degree, several synthetic data samples must be calculated to generate the minority class.
![]()
Where G is the total number of synthetic data, β is a parameter (β∈ [0,1]) that specifies the desired balance level after generating the synthetic data. If the β value is 1, before the generalization process, a fully balanced dataset is created. Next, the Euclidean distance of the minor class samples is found using the CURE method. Initially, the minor class sample distance was dist calculated. Assume, samples〖 (X〗_1=X_11+X_12+⋯,X_1M) and 〖(X〗_2=X_21+X_22+⋯,X_2M):
![]()
The distance between the two data items (p, q) and the two clusters (S, T) are calculated,
![]()
The next step is to set the clustering number c and update and merge the representative points and center based on the smallest distance between the two clusters. Setting the clustering number is used to determine the number of final clusters in the dataset, which helps with clustering; updating the center and representative points helps maintain an accurate representation of the newly merged cluster.
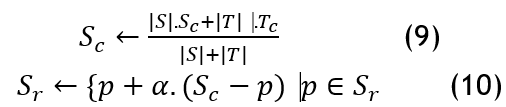
Where the representative set and the center point of the clusters are denoted as S_r and〖 S〗_c ,α=0,5, |S| is the number of data items for the Class S. The class exhibiting the least growth rate is considered to have abnormal points and is scheduled for removal. In cases where the number of representative points exceeds the required amount, the algorithm selects the data point farthest from the cluster's center as the initial representative point. Then, the next representative point chosen is the one that is farthest from the previously selected representative. The algorithm concludes when the number of cluster centres reaches a predetermined threshold, and clusters with minimal samples are eliminated. After determining groups, distributions( r_i ) are calculated in the underlying data to identify regions of high and low density in the feature space. By analyzing the distribution of minority class instances in their local neighbourhoods, ADASYN can target areas with the highest class imbalance.
![]()
Here, r_i represented as an instance ratio (number of majority neighbors/number of minority neighbors). These ratios can determine how many synthetic samples to generate for each instance to address class imbalance in ADASYN adaptively. Instances with higher values r_i are associated with a greater number of synthetic samples to mitigate the imbalance. Next, calculate the number of synthetic data samples that need to be generated for the entire minority class:
![]()
Where, g_i represents the number of synthetic data samples that need to be generated for each instance in the minority class. After generating these synthetic data samples, incorporating them into the dataset to address class imbalance.
The synthetic samples are added to the original dataset, augmenting the minority class. This process increases the size of the minority class and helps balance the class distribution in the dataset. Calculate imbalance ratio and incorporate synthetic samples steps are repeated for each sample in the minority class, ensuring that synthetic samples are generated adaptively based on the local neighborhood characteristics of each instance. This adaptive process continues until it achieves the desired level of balance. The model learns from original and synthetic data and helps address the class imbalance and improve model performance. This process ensures that the synthetic data generation process is controlled and doesn't introduce biases or over-fitting into the model.
Feature selection using IG-IOOA: the IG-IOOA method was developed by combining the IG-based filter and IOOA-based wrapper-based methods. The IG filter selects the important features first, and then the IOOA algorithm reduces the number of selected features. Information Gain (IG) is a widely used filtering technique for effectively selecting highly relevant features in reducing high-dimensional datasets across various applications. IG leverages the concept of entropy to assess the significance of features, quantifying their information gain concerning class labels.
The calculation of gene importance within a specific category can be carried out by analyzing the differences between entropy and conditional entropy, often denoted as IG (Information Gain). Let y denote a discrete random variable attribute containing two possible outputs: relevant and irrelevant for the ideal feature.
![]()
Here, the H binary function represents the logarithmic value, p denotes the probability distribution of the samples Re and ▁Re, is y∈Re and y∈▁Re. On the other hand, there are two events X,Y, X has the value feature x and the definitions of H(Y) and H(Y|X) are provided as follows:
![]()
After the filter-based method selects the important features, the wrapper method of the IOOA algorithm is used to reduce the number of selected features. IOOA is a nature-inspired algorithm based on the decoy behavior of burrowing owls in the presence of predators or other fears near their nests. This algorithm incorporates five key parameters: 〖PP〗_(num,) 〖SP〗_(num,) 〖Dep〗_(nest,) R_(1,) and〖 R〗_(2,). The first three parameters, 〖PP〗_(num,) 〖SP〗_(num,) and〖 Dep〗_(nest,), are associated with the clustering process and nest renewal, while the remaining two, R_(1,) and〖 R〗_(2,) are random values generated from a uniform distribution within the range [0,1].
Stage 1: Initialization: The existing problem, such as the optimization problem and decision parameters, is defined. Further, the IOOA parameters are adjustable, such as 〖OW〗_(n,) representing the number of Owls, 〖PP〗_(num,)denoting the number of primary branches, 〖SP〗_num the number of secondary perches, 〖iter〗_max is the highest iteration number and 〖 Dep〗_nest the deprecated nests’ percentile. It is crucial to observe that the number of primary branches and subordinate branches should match the number of owls, as stated 〖OW〗_(n,)=〖PP〗_(num,)+〖SP〗_(num,) 〖PP〗_num.
Stage 2: Initializing Owl’s Position: Regarding the boundary conditions of a D-dimensional space, the owls are positioned randomly and represented as a matrix;
![]()
Where the individual in the 〖OW〗_n position with dimensions D is represented as O_(〖OW〗_(n,D,).
Stage 3: Sorting: The vector is generated by obtaining the fitness value for the problem for each owl. The classification error or accuracy is considered the fitness metric for each individual. Subsequently, a sorting algorithm is employed to arrange and form clusters according to the attained fitness values, referred to as Ford sort. Each cluster is assigned specific primary and secondary perches. Furthermore, random numbers R_1 and〖 R〗_2 are generated for this stage.
Stage 4: Position Update:-based on the behavior observed in owls, a process where new positions, denoted as〖 OW〗_new are explored within the search space. Initially, an owl explores two positions within a cluster: the next improved perch and the position within that cluster. The owl's objective is to find an improved perch within the remaining unexplored area of the cluster. However, suppose the new position does not offer an advantage over its previous perch or fails to locate a superior one. In that case, the owl chooses to return and remain in its current position. The position update equation is updated by multiplying the function using a parameter 0,1≤ε<1,0, which is adaptively determined based on the number of iterations. This is the improved position update equations.
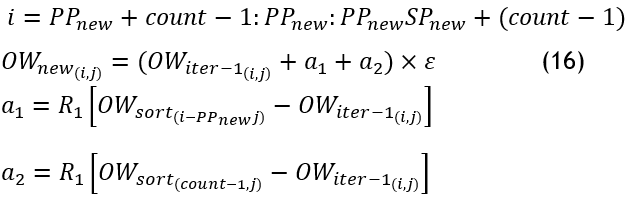
Then, the fitness is evaluated for each new individual.
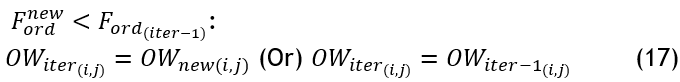
According to the deprecated nests' percentile, the primary branches are also updated as a new perch, 〖OW〗_new^sort obtained from the better perch in position search. If i>round (〖PP〗_new 〖DP〗_new):
![]()
After the above calculation, the fitness is evaluated for each new nest.
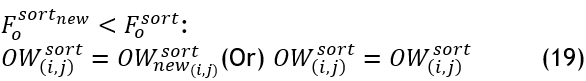
If the new position is not preferable to the prior one, the perch is allocated at its existing location.
Stage 5: Termination: The process proceeds when the highest number of iterations is attained by repeating the location search from the 3rd and 4th stages.
CVD Classification using CRSO-CNN framework: The CRSO algorithm is employed by incorporating the chaotic map functions in the RSO algorithm. This chaotic version is used to initialize the position of the rats in replacement of the random initialization to improve the convergence speed and searching ability. Chaos demonstrates remarkable dynamics and statistical properties with a randomized nature, which means the map function potentially covers the entire region, leading to an effective solution. It also reduces the computational complexity. There are several chaotic map functions, and one of these functions is the iterative chaotic map function. It is mathematically expressed as:
![]()
Here, c=0.7, which is a parameter that controls the behavior of the map, x_(n+1) is the next position and x_n is the current position. Using this chaotic map, the population of rats is initialized in this CRSO as:
![]()
Therefore, the initialization of the population positions is mathematically defined as:
![]()
CRSO conceptualizes the fighting and chasing behavior of the rats with their prey. Rats use their social agnostic behavior to chase their prey in groups. The chasing of the prey is mathematically expressed as:
![]()
Where, P ⃗_i is the position of the rat in the i-th iteration, and P ⃗_best is the position of the optimal rat. And B are the control parameters as they control the exploration and exploitation phases. The control parameters are mathematically defined as:
![]()
Here, B and r are termed as random numbers generated in the range of [0, 2] and [1, 5], respectively and i=0,1,2,…,〖Max〗_iter.
The fighting process of the rats with their prey is mathematically represented as:
![]()
Here, P ⃗_(i+1) is defined as the position of the next rat, which is updated concerning the position of the optimal rat P ⃗_best.
The CNN architecture is optimized using this CRSO algorithm. CNN comprises four main operators: Convolution, pooling layer, fully connected layer, and non-linear activation function.
Convolution layer (CL): It forms the major core of CNN that analyses and extracts the desired features. This convolution task conserves the spatial connection amongst the input data by acquiring the aspects by the kernel function. The outcome of the CL will be the convolved aspect plot. The kernel points are updated automatically based on the optimal structure configuration. The magnitude of the aspect plot is reliant on the depth of the layers.
Non-linear activation (NLA): After the convolution operation, the additional non-linear function is used before creating feature maps. The NLA can be tanh, sigmoid or Rectified Linear Unit (ReLU). This NLA acts as the element-wise task to compromise the negative points of the aspects. In most cases, the sigmoid or ReLU provided better performance.
Pooling layer (PL): Spatial pooling is the sub-sampling or down-sampling process in CNN, performed to reduce the dimensionality of the feature maps. It is similar to the feature reduction process that removes the less important data while retaining vital information. Kinds of pooling are average, max, stochastic and sum pooling, denoted by the pooling numbers 1-4. In most cases, max-pooling provides the most important features.
Fully-connected Layer (FCL): It is a conventional multi-level neural layer employing a softmax initiation utility in the outcome layer. The FCL has the preceding layer nodes interlinked with the succeeding layer nodes. The complex aspects yielded from CL and PL are used by this FCL for labeling the data into classes using past learning knowledge. The process of CRSO to be used for CNN is presented in the following algorithm.
Algorithm 2: CRSO algorithm for tuning CNN parameters
Population Initialization of rats (P_i)
Set Iteration = 0
Initialize the CRSO parameters
Map the CNN parameters to the CRSO solution search
Calculate the fitness and select the best search agent
For each i=0 to n do
Choosing two solutions (x_1,x_2) as parents from the population
Compare the solutions
Update the position of search agents
Update the CRSO parameters
Adjust the out-of-boundary rats
Compute the fitness of each search agent
Update the best solution
Increment Iteration by 1
Until maximum iteration
End for
Return the best solution (CNN configuration) from the population
The top configuration obtained for CNN using CRSO is shown in table 2. The error rate obtained for this configuration is 9,87. For optimal structure, the CRSO-CNN required 3 FCL layers and one EL and CL layer each. This configuration enables CNN to learn deep spatial and temporal features for large-scale datasets. The input dimension is (1, 256, 24) where 1 denotes the input data channel, 256 denotes the number of data, and 24 denotes the time steps to process them.
|
Table 2. Optimal configuration obtained for CRSO-CNN |
|||
|
Layer |
Name |
Parameters |
Dimensions |
|
0 |
Input |
- |
(1, 256, 24) |
|
1 |
EL Activation (ReLU) |
(16, 3, 3) - |
(16, 256, 24) - |
|
2 |
Convolution Pooling Activation (ReLU) |
(64, 3, 3) (2, 2) - |
(64, 64, 6) (64, 32, 3) - |
|
3 |
Flatten |
- |
(1536, ) |
|
4 |
Fully connected |
278 |
(278, ) |
|
5 |
Fully connected |
278 |
(278, ) |
The networks are formed using this configuration. In the next stage, the trained features are used to classify the test data on the similarity, the instance pairs are formed, and the majority voting-based approach is used for classifying the instances.
RESULTS
The proposed method is implemented on the CVD dataset from the UCI repository consisting of the data from Cleveland, Hungary, Switzerland and VA Long Beach (https://archive.ics.uci.edu/ml/datasets/heart+disease). This dataset comprises 303 instances featuring 75 attributes and a single class label. But, out of these 75 attributes, a subset of 14 is commonly employed in most published research. None of these four datasets include the patient names or contact information for privacy considerations. Although the datasets share similar instances, the Cleveland dataset is the most frequently used because it contains fewer missing values than the other three datasets. The Cleveland dataset consists of 5 distinct class values, with 0 absence of heart disease, while 1 to 4 denotes the presence of heart diseases. The other three databases primarily focus on binary classification to distinguish between the presence and absence of heart diseases. The proposed method will use all four databases to validate the pre-processing and classification methods. The performance is evaluated in accuracy, precision, recall, f-measure, error rate, MCC and processing time. Table 3 shows the performance comparison of the proposed method with other existing classification methods.
|
Table 3. Comparison of performance evaluation of the proposed method with the existing classifiers |
||||
|
Methods/metrics |
Cnn |
Rso-cnn |
Crso-cnn |
Proposed IG-IOOA & CRSO-CNN |
|
Cleveland dataset |
||||
|
Accuracy (%) |
97,5653 |
98,0202 |
98,1433 |
99,0099 |
|
Precision (%) |
96,2386 |
97,4478 |
98,1023 |
99,3939 |
|
Recall (%) |
96,5005 |
97,6812 |
97,3068 |
98,9589 |
|
F-Measure (%) |
96,3694 |
97,5644 |
97,7029 |
99,1759 |
|
Error (%) |
2,4347 |
1,9798 |
1,8567 |
0,9901 |
|
MCC |
0,9710 |
0,9725 |
0,9865 |
0,9934 |
|
Time (s) |
7,0120 |
6,4423 |
5,6674 |
3,9030 |
|
Hungarian dataset |
||||
|
Accuracy (%) |
97,3223 |
98,8253 |
98,6519 |
99,6599 |
|
Precision (%) |
96,7445 |
98,1250 |
98,3250 |
99,5927 |
|
Recall (%) |
95,5646 |
96,3549 |
97,5612 |
99,7340 |
|
F-Measure (%) |
96,1509 |
97,2319 |
97,9416 |
99,6333 |
|
Error (%) |
2,6777 |
1,1747 |
1,3481 |
0,3401 |
|
MCC |
0,9531 |
0,9628 |
0,9752 |
0,9946 |
|
Time (s) |
6,2363 |
6,2561 |
4,8596 |
3,4560 |
|
Switzerland dataset |
||||
|
Accuracy (%) |
96,2536 |
97,1269 |
97,2293 |
99,0187 |
|
Precision (%) |
96,3945 |
96,8796 |
97,1356 |
99,7778 |
|
Recall (%) |
96,1030 |
96,3589 |
97,8536 |
99,5833 |
|
F-Measure (%) |
96,2485 |
96,6185 |
97,4933 |
99,6805 |
|
Error (%) |
3,7464 |
2,8731 |
2,7707 |
0,8130 |
|
MCC |
0,9631 |
0,9699 |
0,9726 |
0,9987 |
|
Time (s) |
5,5800 |
4,2548 |
3,1999 |
2,9800 |
|
Va long beach dataset |
||||
|
Accuracy (%) |
97,3695 |
97,2584 |
98,1225 |
99,5000 |
|
Precision (%) |
96,8692 |
97,1256 |
98,1333 |
99,6164 |
|
Recall (%) |
96,3961 |
97,3205 |
97,9987 |
99,5122 |
|
F-Measure (%) |
96,6289 |
97,2230 |
98,0660 |
99,5638 |
|
Error (%) |
2,6305 |
2,7416 |
1,8775 |
0,5000 |
|
MCC |
0,9675 |
0,9722 |
0,9793 |
0,9907 |
|
Time (s) |
7,5982 |
6,2586 |
5,9120 |
3,1020 |
Table 3 shows that the proposed IG-IOOA & CRSO-CNN method has better results. Table 4 presents the evaluation of the proposed IG-IOOA & CRSO-CNN method in comparison to established procedures using the Cleveland dataset. The results affirm the exceptional performance of the IG-IOOA & CRSO-based model when contrasted with existing methods applied to the Cleveland dataset.
|
Table 4. Performance Comparison of IG-IOOA & CRSO-CNN with existing techniques |
|||||||
|
Methods/ Metrics |
Accuracy (%) |
Precision (%) |
Recall (%) |
F-Measure (%) |
Error (%) |
MCC |
Time (s) |
|
MOPSO-RF(11) |
95,21 |
83,5 |
84,26 |
83,88 |
4,79 |
0,8263 |
12,57 |
|
DL-CNN(12) |
97 |
85,60 |
87,72 |
86,65 |
3 |
0,8151 |
25,74 |
|
SSAE-PSO(13) |
96,1 |
92,3 |
82,69 |
87,23 |
3,9 |
0,8512 |
10,6 |
|
TANFIS(14) |
97,76 |
94,6 |
92,74 |
93,66 |
2,24 |
0,9123 |
11,4 |
|
XGBOOST(15) |
91,8 |
88,3 |
95,32 |
91,68 |
8,2 |
0,8926 |
14,8 |
|
MLP-PSO(16) |
94,6 |
95,1 |
86,7 |
90,7 |
5,4 |
0,8695 |
12,76 |
|
GAPSO-RF(17) |
95,6 |
91,68 |
95,2 |
93,41 |
4,4 |
0,9232 |
6,3 |
|
SCGPB(18) |
92,47 |
83,74 |
80 |
86,33 |
7,53 |
0,9547 |
25,9 |
|
BI-LSTM-CNN (19) |
96,66 |
90 |
94,6 |
92,2 |
3,34 |
0,9258 |
26,3 |
|
MABC-SVM(20) |
93,8 |
96,3 |
93,1 |
94,7 |
6,2 |
0,8351 |
27,59 |
|
QPSO-SVM(21) |
96,31 |
98,3 |
89,9 |
93,9 |
3,69 |
0,9736 |
28,7 |
|
Keras-DNN(22) |
90,49 |
97,25 |
95 |
96,11 |
9,51 |
0,9545 |
16,3 |
|
Proposed IG-IOOA & CRSO-CNN |
99 |
99,39 |
98,95 |
99,17 |
0,9901 |
0,9934 |
3,903 |
The results of the comparative analysis in table 3 and 4 demonstrate that the disease classification model based on the proposed IG-IOOA & CRSO-CNN outperforms the models found in the existing literature. These findings emphasize the superiority of the IG-IOOA & CRSO-CNN approach in attaining greater accuracy and superior overall performance when compared to the assessed methods.
DISCUSSION
For the Cleveland dataset, the proposed model increased accuracy by 1,4446 %, 0,9897 %, and 0,866 % compared to CNN, RSO-CNN, and CRSO-CNN methods. For the Hungarian dataset, the achieved accuracy was increased by 2,7651 %, 1,8918 % and 1,008 %, respectively. For the Switzerland dataset, the accuracy was increased by 2,8281 %, 1,8918 % and 1,7957 % and for VA Long Beach Dataset by 2,1306 %, 2,2416 % and 1,3775 % compared to other methods. Similarly, the proposed IG-IOOA & CRSO-CNN-based CVD prediction model achieved good results for precision, recall, f-measure, MCC and error rates. Also, the proposed method reduced the processing time for all four datasets. Consequently, the IG-IOOA & CRSO-CNN method performs better than the CNN, RSO-CNN and CRSO-CNN methods by substantially reducing processing time. These findings show the proposed approach's efficacy and supremacy in handling classification tasks, signifying its promising utility across diverse real-world applications.
The comprehensive comparison of various machine learning models in terms of their performance metrics, including accuracy, precision, recall, F-measure, error rate, Matthews correlation coefficient (MCC), and computational time. Each model has been evaluated on a specific task, presumably a classification problem, and the results showcase their effectiveness in handling the given task. The proposed model, IG-IOOA & CRSO-CNN, outperforms all other models across nearly all metrics. Notably, it achieved a significant increase in accuracy by 3,79 %, 2,01 %, 2,24 %, 7,20 %, 4,40 %, 3,40 %, 6,53 %, 2,34 %, 5,20 %, 2,69 % and 8,51 % compared to MOPSO-RF, DL-CNN, SSAE-PSO, TANFIS, XGBOOST, MLP-PSO, GAPSO-RF, SCGPB, BI-LSTM-CNN, MABC-SVM, QPSO-SVM and Keras-DNN. The proposed model remarkably reduced the computational time required for analysis compared to several counterparts. It demonstrates a considerable decrease in computational time relative to 8,667s, 21,837s, 6,697s, 7,497s, 10,897s, 8,857s, 2,397s, 21,997s, 22,397s, 23,687s, 24,797s and 12,397s. This reduction in computational overhead can be crucial for real-time applications or large-scale datasets. Overall, the proposed IG-IOOA and CRSO-CNN model showcased competitive performance across various metrics while offering significant computational advantages compared to existing models. Its robust performance makes it a promising for a wide array of classification tasks.
The proposed model exhibited enhanced input quality and addressed issues like class imbalance outliers and missing values. The hybrid model also selected optimal features and reduced redundancy with improved model performance. The proposed model achieves high accuracy in CVD prediction while maintaining low complexity, making it suitable for practical deployment in clinical settings. By combining efficient feature selection, robust classification, and streamlined pre-processing, the model offers a promising solution for early diagnosis of cardiovascular disease.
CONCLUSIONS
This paper introduces an effective disease classification model that combines efficient pre-processing techniques with advanced machine learning classifiers. The proposed framework employs an IG-based filter method and IOOA wrapper-based method for feature selection on pre-processed data to reduce dimensionality and highlight the most relevant attributes for classification. Subsequently, the CRSO-CNN machine learning classifier is utilized to classify individual patient data. When evaluated against benchmark datasets, the IG-IOOA and CRSO-CNN-based model demonstrates enhanced disease classification accuracy and reduced model complexity. Comparative analyses with existing methods further validate the effectiveness of the proposed model. Future research will explore the potential for detecting heart diseases in multiple source datasets and consider applying this model to other disease datasets.
REFERENCES
1. Ghorashi S, Rehman K, Riaz A, Alkahtani HK, Samak AH, Cherrez-Ojeda I, Parveen A. Leveraging regression analysis to predict overlapping symptoms of cardiovascular diseases. IEEE Access. 2023 Jun 14.
2. Inamdar AA, Inamdar AC. Heart failure: diagnosis, management and utilization. Journal of clinical medicine. 2016 Jun 29;5(7):62.
3. Sun R, Liu M, Lu L, Zheng Y, Zhang P. Congenital heart disease: causes, diagnosis, symptoms, and treatments. Cell biochemistry and biophysics. 2015 Jul;72:857-60.
4. Fitriyani NL, Syafrudin M, Alfian G, Rhee J. HDPM: an effective heart disease prediction model for a clinical decision support system. IEEE Access. 2020 Jul 20;8:133034-50.
5. Kitano T, Kovács A, Nabeshima Y, Tokodi M, Fábián A, Lakatos BK, Takeuchi M. Prognostic value of right ventricular strains using novel three-dimensional analytical software in patients with cardiac disease. Frontiers in Cardiovascular Medicine. 2022 Feb 25;9:837584.
6. Yoo H, Chung K, Han S. Prediction of cardiac disease-causing pattern using multimedia extraction in health ontology. Multimedia Tools and Applications. 2021 Nov;80(26):34713-29.
7. Ribeiro JM, Astudillo P, de Backer O, Budde R, Nuis RJ, Goudzwaard J, Van Mieghem NM, Lumens J, Mortier P, Mattace-Raso F, Boersma E. Artificial intelligence and transcatheter interventions for structural heart disease: a glance at the (near) future. Trends in cardiovascular medicine. 2022 Apr 1;32(3):153-9.
8. Sarker IH. Deep learning: a comprehensive overview on techniques, taxonomy, applications and research directions. SN Computer Science. 2021 Nov;2(6):420.
9. McInnes L, Healy J, Astels S. hdbscan: Hierarchical density based clustering. J. Open Source Softw.. 2017 Mar 21;2(11):205.
10. He H, Bai Y, Garcia EA, Li S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In2008 IEEE international joint conference on neural networks (IEEE world congress on computational intelligence) 2008 Jun 1 (pp. 1322-1328). Ieee.
11. Asadi S, Roshan S, Kattan MW. Random forest swarm optimization-based for heart diseases diagnosis. Journal of biomedical informatics. 2021 Mar 1;115:103690.
12. Mehmood A, Iqbal M, Mehmood Z, Irtaza A, Nawaz M, Nazir T, Masood M. Prediction of heart disease using deep convolutional neural networks. Arabian Journal for Science and Engineering. 2021 Apr;46(4):3409-22.
13. Mienye ID, Sun Y. Improved heart disease prediction using particle swarm optimization based stacked sparse autoencoder. Electronics. 2021 Sep 25;10(19):2347.
14. Sekar J, Aruchamy P, Sulaima Lebbe Abdul H, Mohammed AS, Khamuruddeen S. An efficient clinical support system for heart disease prediction using TANFIS classifier. Computational Intelligence. 2022 Apr;38(2):610-40.
15. Budholiya K, Shrivastava SK, Sharma V. An optimized XGBoost based diagnostic system for effective prediction of heart disease. Journal of King Saud University-Computer and Information Sciences. 2022 Jul 1;34(7):4514-23.
16. Al Bataineh A, Manacek S. MLP-PSO hybrid algorithm for heart disease prediction. Journal of Personalized Medicine. 2022 Jul 25;12(8):1208.
17. El-Shafiey MG, Hagag A, El-Dahshan ES, Ismail MA. A hybrid GA and PSO optimized approach for heart-disease prediction based on random forest. Multimedia Tools and Applications. 2022 May;81(13):18155-79.
18. Paul B, Karn B. Heart disease prediction using scaled conjugate gradient backpropagation of artificial neural network. Soft Computing. 2023 May;27(10):6687-702.
19. Shrivastava PK, Sharma M, Kumar A. HCBiLSTM: A hybrid model for predicting heart disease using CNN and BiLSTM algorithms. Measurement: Sensors. 2023 Feb 1;25:100657.
20. Yaqoob MM, Nazir M, Khan MA, Qureshi S, Al-Rasheed A. Hybrid classifier-based federated learning in health service providers for cardiovascular disease prediction. Applied Sciences. 2023 Feb 1;13(3):1911.
21. Elsedimy EI, AboHashish SM, Algarni F. New cardiovascular disease prediction approach using support vector machine and quantum-behaved particle swarm optimization. Multimedia Tools and Applications. 2024 Mar;83(8):23901-28.
22. Almazroi AA, Aldhahri EA, Bashir S, Ashfaq S. A clinical decision support system for heart disease prediction using deep learning. IEEE Access. 2023 Jun 12.
FINANCING
"The authors did not receive financing for the development of this research.
CONFLICT OF INTEREST
The authors declare that there is no conflict of interest.
AUTHORSHIP CONTRIBUTION
Conceptualization: Sasirega. D, Dr.Krishnapriya.V.
Formal analysis: Sasirega. D.
Research: Sasirega. D and Dr.Krishnapriya.V.
Methodology: Sasirega. D, Dr.Krishnapriya.V.
Drafting - original draft: Sasirega. D.
Writing - proofreading and editing: Sasirega. D, Dr.Krishnapriya.V.