doi: 10.56294/dm2024.348

ORIGINAL

Sociocognitive configuration: meanings and creations in the mathematical learning of middle school students

Configuración sociocognitiva: significaciones y creaciones en el aprendizaje matemático de estudiantes de educación media

María José Parada Carreño¹ *, Antonio José Bravo Valero² *, Juan Diego Hernández Albarracín³ *

¹Institución Educativa Oriental No. 26. San José de Cúcuta - Colombia.

²Universidad Simón Bolívar. Facultad de Ciencias Básicas y Biomédicas, Centro de Crecimiento Empresarial – MACONDOLAB. Cúcuta, Colombia.

³Universidad Simón Bolívar. Facultad de Ciencias Jurídicas y Sociales, Centro de Investigación en Estudios Fronterizos. Cúcuta, Colombia.

Citar como: Parada Carreño MJ, Bravo Valero AJ, Hernández Albarracín JD. Sociocognitive configuration: meanings and creations in the mathematical learning of middle school students. Data and Metadata. 2024; 3:.348. https://doi.org/10.56294/dm2024.348

Enviado: 14-02-2024                   Revisado: 26-05-2024                   Aceptado: 30-09-2024                Publicado: 01-10-2024

Editor: Adrián Alejandro Vitón-Castillo

Autor para la correspondencia: María José Parada Carreño *

ABSTRACT

The study explores the socio-cognitive configuration in the mathematical learning of middle school students, relating cognitive processes to the social interactions that shape perceptions and performance in mathematics. A qualitative approach was adopted to delve into students’ subjective experiences. Meaningful interactions revealed in the classroom enhance mathematical understanding and foster critical and problem-solving skills. The socio-cognitive configuration achieved evidence that mathematical cognition is deeply affected and defined by its social context and educational practices. This study underscores the importance of integrating students’ personal and collective meanings in mathematical learning to foster a holistic pedagogical approach to both the transmission of knowledge and its social and personal relevance, which transforms mathematics teaching by making it more applicable to students’ real-life challenges and contexts.

Keywords: Sociocognitive Configuration; Imaginary Significations; Creations in Learning; Social Interactions; Mathematical Learning.

RESUMEN

El estudio explora la configuración sociocognitiva en el aprendizaje matemático de estudiantes de media, relacionando los procesos cognitivos con las interacciones sociales que moldean las percepciones y el desempeño en matemáticas. Se adoptó un enfoque cualitativo para profundizar en las experiencias subjetivas de los estudiantes. Las interacciones significativas reveladas en el aula mejoran la comprensión matemática y fomentan habilidades críticas y de resolución de problemas. La configuración sociocognitiva alcanzada evidencia que la cognición matemática es profundamente afectada y definida por su contexto social y las prácticas educativas. Este estudio subraya la importancia de integrar las significaciones personales y colectivas de los estudiantes en el aprendizaje matemático para fomentar un enfoque pedagógico holístico tanto para la transmisión del conocimiento como su relevancia social y personal, lo que transforma la enseñanza de las matemáticas haciendo que sea más aplicable a los desafíos y contextos de la vida real de los estudiantes.

Palabras clave: Configuración Sociocognitiva; Significaciones Imaginarias; Creaciones en el Aprendizaje; Interacciones Sociales; Aprendizaje Matemático.

INTRODUCCIÓN

La interacción entre los procesos cognitivos individuales y los factores sociales en un contexto de aprendizaje o de desarrollo humano establecen la configuración sociocognitiva de un individuo.⁽¹⁾ Esta idea encapsula cómo las estructuras cognitivas de una persona, es decir, su manera de pensar, entender y procesar información, están influenciadas y moldeadas por el entorno, que incluye las interacciones con otros, las normas culturales, y las instituciones educativas.⁽²⁾ La configuración sociocognitiva es un marco útil para entender la interdependencia entre el pensamiento individual y los contextos sociales en los que este pensamiento se desarrolla y manifiesta.

La teoría de las significaciones imaginarias sociales resalta cómo la interacción entre los procesos cognitivos individuales y los factores sociales, detallada por Bandura⁽¹⁾ y Salomon⁽²⁾, juega un papel crucial en la comprensión humana. Las significaciones colectivas emergen y se sustentan dentro de una comunidad, incluyendo símbolos, mitos y valores compartidos.⁽³⁾ Estos elementos permiten tanto comprender y dar sentido al mundo,⁽⁴⁾ lo que en consecuencia influye en la configuración de estructuras cognitivas y en la manera de procesar información.

Este marco conceptual se alinea con la idea de la configuración sociocognitiva, subrayando cómo la cognición individual y el contexto social y se entrelazan de manera que cada uno moldea y redefine al otro.⁽⁵⁾ Como lo plantean Pintos⁽⁶⁾ y García-Muñoz y Gómez-Gallego⁽⁷⁾, las significaciones imaginarias actúan como prismas interpretativos del entorno y las experiencias. Según Murcia Peña y Jaramillo Ocampo⁽⁸⁾, estas significaciones afectan el cómo se enseña y se aprende, y pueden servir como catalizadores para métodos pedagógicos que reconocen y utilizan estos repertorios de sentido de manera constructiva.

Las creaciones humanas, como elementos básicos en la configuración sociocognitiva, no se pueden observar únicamente como reflejos o técnicas. Castoriadis y Vicens⁽⁹⁾ resaltan cómo cada cultura crea e instituye valores propios que influyen profundamente en la orientación de la vida y en sus motivaciones. Estas creaciones, lejos de ser simples reproducciones o respuestas automáticas a estímulos, representan genuinas innovaciones del tejido social que afectan y definen la naturaleza de las interacciones y los procesos cognitivos individuales y colectivos.

La dialéctica entre el legein y el teukhein descrita por Castoriadis y Vicens⁽⁹⁾ refleja la interacción entre el decir y el hacer en el ámbito social, en el cual cada acto y cada palabra son creaciones que emergen del imaginario social y al mismo tiempo lo transforman. La comprensión profunda de la configuración sociocognitiva y su interrelación con las significaciones imaginarias y las creaciones en el contexto educativo, esta investigación busca explorar cómo estos elementos se manifiestan en el aprendizaje de las matemáticas en estudiantes de educación media.

MÉTODO

Diseño metódico

Esta investigación se guía por un enfoque cualitativo⁽¹⁰⁾ debido a su capacidad para profundizar en las experiencias subjetivas de los individuos, permitiendo una comprensión detallada de los procesos cognitivos y sociales que conforman la educación matemática.

La recolección de datos se realizó con entrevistas semiestructuradas.⁽¹¹⁾ El guion de entrevista se basó en una integración teórica de la configuración sociocognitiva, significaciones y creaciones de la realidad del aprendizaje matemático en la educación media.

Tal fundamentación teórica se operacionaliza mediante un sistema de categorías que estructura los elementos del fenómeno de estudio: el aprendizaje de las matemáticas en el contexto de educación media. La Figura 1 ilustra el sistema de categorías para la comprensión de las áreas a explorar y documentar. Un proceso de validación confirmó la claridad, precisión de las preguntas en la exploración de los constructos teóricos establecidos.⁽¹²⁾

Participantes

El estudio se centró en un grupo de 20 estudiantes de grados 10 y 11 de la Institución Educativa Colegio Oriental N. 26 de Cúcuta, Norte de Santander en Colombia. Estos estudiantes fueron seleccionados mediante un muestreo por conveniencia debido a la accesibilidad y la disposición de los estudiantes para participar en el estudio.^(13,14) Cada estudiante proporcionó narrativas personales acerca de cómo las matemáticas influyen y se integran en su vida diaria y su desarrollo académico.⁽¹⁵⁾

Técnica de Análisis de Narrativas

Se empleó la teoría fundamentada⁽¹⁶⁾ como técnica útil para comprender fenómenos complejos en la identificación de patrones dentro de las narrativas. Inicialmente, se extrajeron citas de las percepciones del aprendizaje matemático, las cuales fueron codificadas y agrupadas en familias de códigos facilitando la síntesis de datos.⁽¹⁷⁾ Durante el análisis, se dio apertura a categorías emergentes para no restringirlo a las categorías predefinidas. Esto aseguró la captura de la complejidad y la diversidad de las perspectivas con apoyo del software NVivo. El software facilitó la gestión de datos proporcionando herramientas de la codificación, recuperación y visualización de relaciones entre categorías.⁽¹⁸⁾

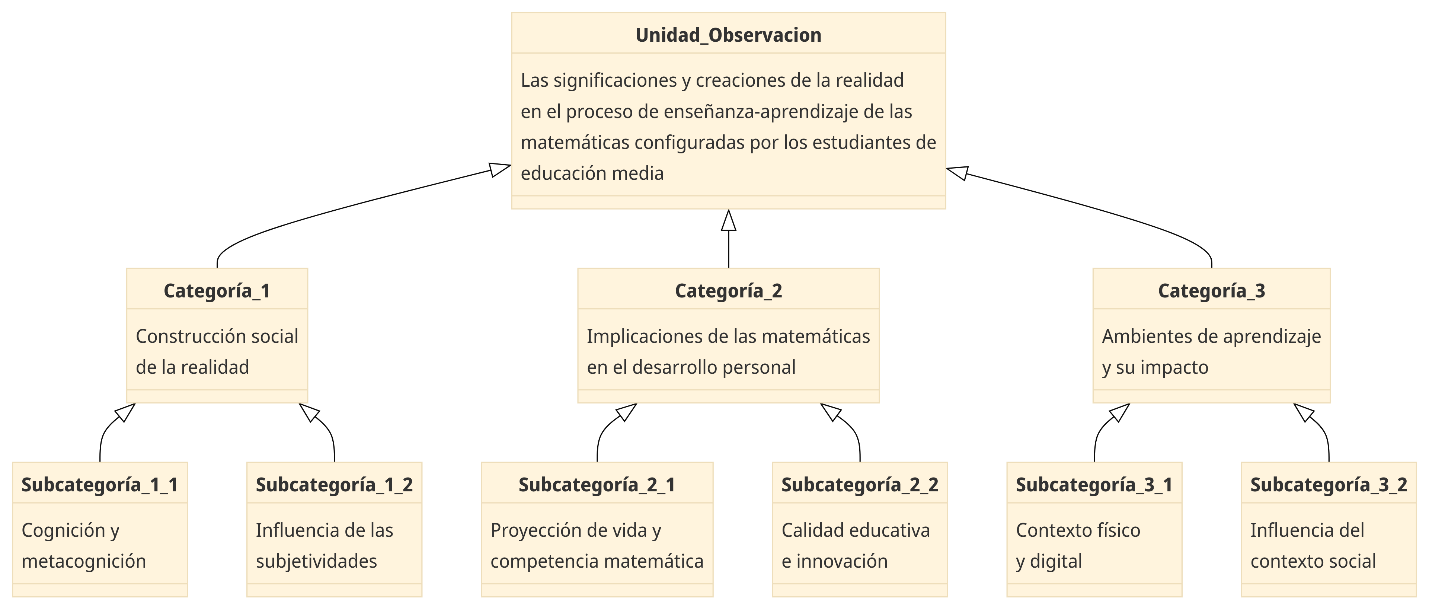
Figura 1. Categorías para el análisis del aprendizaje matemático

RESULTADOS

La tabla 1 expone los hallazgos siguiendo las categorías delineadas durante el análisis, cada uno profundizando en diferentes dimensiones de cómo las matemáticas configuran y son configuradas por las significaciones y creaciones de los estudiantes.

Tabla 1. Elementos que impactan las matemáticas en la educación y la vida cotidiana
Hallazgo	Descripción
Aspectos cognitivos y metodológicos	Las matemáticas son apreciadas tanto su utilidad práctica como por su belleza y rigor lógico intrínsecos.
Cosmovisión y significaciones personales	La cosmovisión matemática impacta en las percepciones individuales y colectivas al relacionarlos con esta ciencia.
Ambientes de aprendizaje	El ambiente físico y social es crucial para el éxito, la comodidad del aula.
Contexto digital	Los Recursos Educativos Digitales (RED) enriquecen el aprendizaje.
Implicaciones prácticas de las matemáticas	La competencia es fundamental en la academia y la vida diaria.
Innovación educativa	Métodos innovadores transforman la educación haciendo el aprendizaje más atractivo y accesible.

La tabla 2 presenta una colección de citas extraídas de las narrativas que ilustran tanto perspectivas positivas como desafíos enfrentados en aspectos clave del aprendizaje.

Tabla 2. Percepciones de estudiantes sobre el aprendizaje de matemáticas
Hallazgo	Citas positivas	Citas negativas
Aspectos cognitivos y metodológicos	“Para mí la matemática sirve mucho en la vida, … “. (Participante_4).	“No se interesan por qué cada uno de los estudiantes esté animado a aprender…”. (Participante_2).
Cosmovisión y significaciones personales	“Tienen un gran significado puesto que están en cada área de la vida…”. (Participante_1).	“No tiene el más mínimo significado de mi vida cotidiana…”. (Participante_19).
Ambientes de aprendizaje	“El salón está normal, las clases de matemáticas la explican bien”. (Participante_3).	“Me agobia el calor y evita que me concentre… “. (Participante_16).
Contexto digital	“La verdad es muy beneficioso y de mucha ayuda la tecnología ya que podemos ver videos …”. (Participante_7).	“En nada porque no entiendo ni cuando veo videos”. (Participante_8).
Implicaciones prácticas	“Gracias a las matemáticas se me ha facilitado entender temas más complejos...” (Participante_5).	“Creo que las matemáticas son importantes en la vida diaria…”. (Participante_12).
Innovación educativa	“La competitividad se hacía por aprender y ser mejor…”. (Participante_10).	“Ninguna innovadora, sólo método tradicional”. (Participante_16).

Las significaciones se refieren a cómo los estudiantes perciben el rol de las matemáticas en su vida diaria y académica, y cómo estas percepciones influencian su cosmovisión y actitudes hacia la disciplina. Las creaciones describen las diversas maneras en que las percepciones de los estudiantes se materializan en comportamientos, decisiones académicas y profesionales, y métodos de aprendizaje. La tabla 3 muestra las significaciones y creaciones obtenidas de las percepciones de los estudiantes de educación media.

Tabla 3. Significaciones y creaciones: percepciones en contextos educativos y personales
Significación	Creación
Percepción de las matemáticas día a día	Valor asignado más allá de su utilidad
Emociones y percepciones individuales	Experiencias educativas formativas
Efectos de condiciones subóptimas de aprendizaje	Efectos en trayectorias académicas y profesionales
Influencia de las matemáticas en decisiones	Aplicación en contextos variados
Reacciones hacia la enseñanza tradicional	Contribución al desarrollo social y personal
Opiniones sobre la eficacia de los RED	Cambios en la carrera impulsados por matemáticas
Impacto de factores externos y ambientales en el aprendizaje
Impacto del entorno	Desarrollo personal atribuido al aprendizaje matemático
Efecto del entorno físico en la concentración
Valoración colectiva de las matemáticas	Métodos de aprendizaje individuales
Mejora de métodos de enseñanza tradicionales	Adopción de enfoques educativos novedosos
Importancia de la competencia y autoeficacia en el aprendizaje	Fomento de habilidades prácticas
Experiencias educativas gratificantes	Preferencias por estrategias de aprendizaje transmedia
Desarrollo personal y emocional

Las creaciones destacan la capacidad de cada cultura educativa para forjar valores que influyan en la orientación de la vida y sus motivaciones.⁽¹⁹⁾

DISCUSIÓN

La configuración sociocognitiva en el aprendizaje matemático de los estudiantes de educación media aborda profundamente las interacciones dinámicas entre la cognición individual y el contexto sociocultural.⁽²⁰⁾ Como señalan Bandura⁽¹⁾ y Salomon⁽²⁾, el entorno social en el que los estudiantes interactúan afecta significativamente su forma de procesar y utilizar el conocimiento matemático, un concepto que es fundamental en la comprensión de la configuración sociocognitiva.

La configuración sociocognitiva no solo facilita el aprendizaje de conceptos matemáticos, sino que también fomenta la integración de estos conceptos en la vida cotidiana de los estudiantes. Esta integración es crucial para el desarrollo de una competencia matemática práctica y aplicada. Es fundamental reconocer que los procesos cognitivos individuales son moldeados por las interacciones sociales, y estas interacciones pueden ser diseñadas pedagógicamente para maximizar el aprendizaje y la retención de conceptos matemáticos.

Las significaciones imaginarias, como construcciones sociales y culturales, juegan un papel vital en cómo los estudiantes perciben y valoran las matemáticas. Estas significaciones pueden influir en la motivación y el interés de los estudiantes por la materia. Por ejemplo, un estudiante que ve las matemáticas como una herramienta para resolver problemas reales puede estar más motivado a aprender que uno que las ve como un conjunto de reglas abstractas sin aplicación práctica.

La investigación destaca cómo las matemáticas funcionan como una construcción social influenciada por interacciones significativas dentro del entorno educativo.⁽²¹⁾ Según Cerchiaro et al.⁽²²⁾, estas interacciones no solo facilitan la comprensión matemática, sino que también promueven habilidades de pensamiento crítico y resolución de problemas, aspectos que son esenciales para la adaptabilidad y flexibilidad cognitiva.⁽²³⁾ Estos hallazgos destacan la capacidad de los estudiantes para aplicar matemáticas de manera efectiva en diversas situaciones, fundamental para su desarrollo académico y personal.

La implementación de prácticas pedagógicas innovadoras, que integren las experiencias y significaciones personales y colectivas de los estudiantes, puede enriquecer significativamente su aprendizaje matemático. Estas prácticas deben incluir métodos que promuevan la colaboración, la resolución de problemas en contextos reales y el uso de recursos digitales educativos (RED). Al fomentar un entorno de aprendizaje interactivo y contextualizado, se puede mejorar no solo la comprensión matemática, sino también la aplicación práctica de los conocimientos adquiridos.

La investigación también explora cómo las significaciones imaginarias⁽³⁾ forman un esquema de percepción que dan sentido a su mundo matemático. Esta dimensión sociocultural se refleja en la forma en que los estudiantes valoran y aplican sus conocimientos matemáticos tanto en contextos académicos como en su vida cotidiana. Los educadores deben tener en cuenta cómo las percepciones colectivas e individuales afectan la relación estudiante-matemáticas.

La calidad del entorno educativo, tanto físico como social, es un factor determinante en la eficacia del aprendizaje matemático. Un ambiente de aprendizaje cómodo y estimulante, junto con un apoyo social adecuado, puede facilitar la concentración y el compromiso de los estudiantes con las matemáticas. Además, el uso de tecnologías digitales puede proporcionar a los estudiantes acceso a múltiples recursos y perspectivas, enriqueciendo su experiencia educativa.

Cerrando la discusión, es claro que un enfoque integrador de teorías educativas con prácticas pedagógicas innovadoras significativamente enriquece la experiencia educativa en matemáticas. Implementar y evaluar enfoques educativos integradores y prácticos no solo mejora el rendimiento académico de los estudiantes, sino que también promueve una comprensión más profunda y aplicada de las matemáticas. Esto, a su vez, puede empoderar a los estudiantes para utilizar las matemáticas como una herramienta para comprender y transformar su contexto social y personal.^{(21,24, 25, 26)}

CONCLUSIÓN

El estudio revela cómo las matemáticas son configuradas por los estudiantes no solo como conocimientos abstractos sino también como herramientas vitales que se integran en su interpretación y actuación dentro de su mundo cotidiano y futuro. Esta investigación subraya la comprensión de las matemáticas como una construcción social, influenciada significativamente por las interacciones dentro del entorno educativo y las normas culturales y sociales predominantes. La influencia de las interacciones sociales, la calidad del entorno educativo⁽²⁷⁾ y la pertinencia de los métodos de enseñanza son factores determinantes que impactan directamente la relación de los estudiantes en los procesos de aprendizaje.⁽²⁸⁾

La configuración de las matemáticas por parte de los estudiantes de educación media presenta tanto aspectos positivos como negativos que influyen significativamente en cómo perciben y aplican las matemáticas en su aprendizaje y vida cotidiana. Los aspectos negativos corresponden con, presión y ansiedad, desconexión con la realidad, influencia de estereotipos, y metodologías de enseñanza rígidas. Los aspectos positivos, habilidades críticas y resolutivas, empoderamiento, flexibilidad cognitiva, y preparación para el futuro. Estos insights son cruciales para diseñar intervenciones que no solo aborden los desafíos, sino que también aprovechen las oportunidades para enriquecer la experiencia educativa de los estudiantes.

REFERENCIAS

1. Bandura A. Self-efficacy: the exercise of control. New York: W H Freeman & Co; 1997.

2. Salomon G. Cogniciones distribuidas: consideraciones psicológicas y educativas. Amorrortu; 2001.

3. Castoriadis C. El imaginario social instituyente. Zona Erógena. 1997;35(9):1–9.

4. Cegarra J. Fundamentos teórico epistemológicos de los imaginarios sociales. Cinta de Moebio. 2012; (43). Disponible en: http://www.moebio.uchile.cl/43/cegarra.html

5. Kahl S, Kopp S. Intertwining the social and the cognitive loops: socially enactive cognition for human-compatible interactive systems. Phil Trans R Soc B. 2023;378(1875):20210474. https://doi.org/10.1098/rstb.2021.0474

6. Pintos JL. Los imaginarios sociales: la nueva construcción de la realidad social. Editorial Sal Terrae; 1995.

7. García-Muñoz CM, Gómez-Gallego RÁ. Aproximación epistemológica a los imaginarios sociales como categoría analítica en las ciencias sociales. Rev Guillermo Ockham. 2021;19(2):219–32. https://doi.org/10.21500/22563202.4807

8. Murcia Peña N, Jaramillo Ocampo D. La Escuela con mayúscula: Configurando una Escuela para el re-conocimiento. Cárol Castaño Trujillo. 2017;35(9):153-178.

9. Castoriadis C, Vicens A. La institución imaginaria de la sociedad. Tusquets; 2013

10. Creswell JW. Research design: qualitative, quantitative, and mixed methods approaches. SAGE Publications; 2013.

11. Patton MQ. Qualitative research & evaluation methods: integrating theory and practice. SAGE Publications; 2015.

12. Cohen L, Manion L, Morrison K. Research methods in education. Routledge; 2018.

13. Bryman A. Social research methods. Oxford University Press; 2016.

14. Maxwell JA. Qualitative research design: an interactive approach. SAGE Publications; 2013.

15. Silverman D. Doing qualitative research. SAGE Publications; 2017.

16. Corbin J, Strauss A. Basics of qualitative research: techniques and procedures for developing grounded theory. SAGE Publications; 2015.

17. Saldaña J. The coding manual for qualitative researchers. SAGE Publications; 2016.

18. Dhakal K. NVivo. Jmla. 2022;110(2). https://doi.org/10.5195/jmla.2022.1271

19. Ylimaki RM, Brunderman LA. Values, Culture and Context. En: Ylimaki RM, Brunderman LA, editores. Evidence-Based School Development in Changing Demographic Contexts Cham: Springer International Publishing; 2022. p. 43–53. https://doi.org/10.1007/978-3-030-76837-9_3

20. Dressel M. Models of science and society: transcending the antagonism. Humanit Soc Sci Commun. 2022;9(1):241. https://doi.org/10.1057/s41599-022-01261-x

21. Vygotsky L. Mind in society: the development of higher psychological processes. Cambridge: Harvard University Press; 1978.

22. Cerchiaro Ceballos E, Barras Rodríguez RA, Breidis Nayely Curiel Gómez BN, Bustamante Meza LY. Metacognición y resolución de problemas en niños escolarizados. 2021;1–23. https://doi.org/10.32457/ejep.v14i2.1570

23. Olhaberry M, Sieverson C. Desarrollo socio-emocional temprano y regulación emocional. Revista Médica Clínica Las Condes. 2022; 33(4):358–66. https://doi.org/10.1016/j.rmclc.2022.06.002

24. Giroux H. On critical pedagogy. London: Bloomsbury Publishing; 2020.

25. Kozlowski JS, Chamberlin SA, Mann E. Factors that Influence Mathematical Creativity. The Mathematics Enthusiast. 2019;16(1–3):505–40. https://doi.org/10.54870/1551-3440.1471

26. Olivares D, Lupiáñez JL, Segovia I. Roles and characteristics of problem solving in the mathematics curriculum: a review. International Journal of Mathematical Education in Science and Technology 2021; 52(7):1079–96. https://doi.org/10.1080/0020739X.2020.1738579

27. Hernández-Albarracín JD, Ramírez-Lindarte MD, Bravo AJ. Hacia un nuevo lugar de enunciación: aportes intersubjetivos sobre la calidad de la educación en norte de Santander. Una perspectiva desde la teoría fundamentada. Análisis Político. 2023; 36(107):89–108. Disponible en: https://doi.org/10.15446/anpol.v36n107.112547

28. Brighenti AM, Sabetta L. Activated. Towards a sociology of reaction. European Journal of Social Theory. 2024; 13684310241230168. https://doi.org/10.1177/13684310241230167

FINANCIACIÓN

Ninguna.

CONFLICTO DE INTERESES

Ninguno.

CONTRIBUCIÓN DE AUTORÍA

Conceptualización: María José Parada Carreño, Antonio José Bravo Valero.

Curaduría de datos: María José Parada Carreño, Antonio José Bravo Valero.

Análisis Formal: María José Parada Carreño, Antonio José Bravo Valero.

Investigación: María José Parada Carreño, Antonio José Bravo Valero.

Metodología: María José Parada Carreño, Antonio José Bravo Valero.

Administración del proyecto: María José Parada Carreño, Antonio José Bravo Valero.

Recursos: María José Parada Carreño, Antonio José Bravo Valero.

Software: María José Parada Carreño, Antonio José Bravo Valero.

Supervisión: María José Parada Carreño, Antonio José Bravo Valero.

Validación: María José Parada Carreño, Antonio José Bravo Valero.

Visualización: María José Parada Carreño, Antonio José Bravo Valero.

Redacción (borrador original): María José Parada Carreño, Antonio José Bravo Valero, Juan Diego Hernández Albarracín.

Redacción (revisión y edición): María José Parada Carreño, Antonio José Bravo Valero, Juan Diego Hernández Albarracín.