doi: 10.56294/dm2024.358

ORIGINAL

Deep Revamped Quantum Convolutional Neural Network on Fashion MNIST Dataset

Red neuronal convolucional cuántica profunda renovada en el conjunto de datos MNIST de moda

Meshal Alharbi¹ *, Sultan Ahmad¹ *

¹Department of Computer Science, College of Computer Engineering and Sciences Prince Sattam Bin Abdulaziz University. Alkharj 11942, Saudi Arabia.

Cite as: Alharbi M, Sultan A. Deep Revamped Quantum Convolutional Neural Network on Fashion MNIST Dataset. Data and Metadata. 2024; 3:.358. https://doi.org/10.56294/dm2024.358

Submitted: 18-01-2024                   Revised: 07-05-2024                   Accepted: 11-09-2024                 Published: 12-09-2024

Editor: Adrián Alejandro Vitón Castillo

Corresponding Author: Meshal Alharbi *

ABSTRACT

Introduction: image classification stands as a pivotal undertaking within the domain of computer vision technology. Primarily, this task entails the processes of image augmentation and segmentation, which are executed by various neural network architectures, including multi-layer neural networks, artificial neural networks, and perceptron networks. These image classifiers employ distinct hyperparameters for the prediction and identification of objects. Nevertheless, these neural networks exhibit susceptibility to issues such as overfitting and a lack of interpretability when confronted with low-quality images.

Objective: these limitations can be mitigated through the adoption of Quantum Computing (QC) methodologies, which offer advantages such as rapid execution speed, inherent parallelism, and superior resource utilization.

Method: this approach aims to ameliorate the challenges posed by conventional Machine Learning (ML) methods. Convolutional Neural Networks (CNNs) are instrumental in reducing the number of parameters while preserving the quality of dataset images. They also possess the capability to automatically discern salient features and maintain robustness in noisy environments. Consequently, a novel approach known as Deep Revamped Quantum CNN (DRQCNN) has been developed and implemented for the purpose of categorizing images contained within the Fashion MNIST dataset, with a particular emphasis on achieving heightened accuracy rates.

Results: in order to assess its efficacy, this proposed method is systematically compared with the traditional Artificial Neural Network (ANN). DRQCNN leverages quantum circuits as convolutional filters with a weight adjustment mechanism for multi-dimensional vectors.

Conclusions: this innovative approach is designed to enhance image classification accuracy and overall system effectiveness. The efficacy of the proposed system is evaluated through the analysis of key performance metrics, including F1-score, precision, accuracy, and recall.

Keywords: Image Classification; Quantum Computing; Convolutional Neural Network; Weight Adjustments; Fashion MNIST.

RESUMEN

Introducción: la clasificación de imágenes es una tarea fundamental en el ámbito de la tecnología de visión por ordenador. Principalmente, esta tarea implica los procesos de aumento y segmentación de imágenes, que son ejecutados por diversas arquitecturas de redes neuronales, incluyendo redes neuronales multicapa, redes neuronales artificiales y redes perceptrón. Estos clasificadores de imágenes emplean distintos hiperparámetros para la predicción e identificación de objetos. Sin embargo, estas redes neuronales muestran susceptibilidad a problemas como el sobreajuste y la falta de interpretabilidad cuando se enfrentan a imágenes de baja calidad.

Objetivo: estas limitaciones pueden mitigarse mediante la adopción de metodologías de Computación Cuántica (CC), que ofrecen ventajas como una rápida velocidad de ejecución, un paralelismo inherente y una utilización superior de los recursos.

Método: este enfoque tiene como objetivo mejorar los desafíos planteados por los métodos convencionales de Aprendizaje Automático (ML). Las redes neuronales convolucionales (CNN) permiten reducir el número de parámetros y preservar la calidad de las imágenes de los conjuntos de datos. También poseen la capacidad de discernir automáticamente características destacadas y mantener la solidez en entornos ruidosos. En consecuencia, se ha desarrollado e implementado un nuevo enfoque conocido como Deep Revamped Quantum CNN (DRQCNN) con el fin de categorizar las imágenes contenidas en el conjunto de datos Fashion MNIST, haciendo especial hincapié en lograr mayores índices de precisión.

Resultados: para evaluar su eficacia, este método propuesto se compara sistemáticamente con la Red Neuronal Artificial (RNA) tradicional. DRQCNN aprovecha los circuitos cuánticos como filtros convolucionales con un mecanismo de ajuste de pesos para vectores multidimensionales.

Conclusiones: este enfoque innovador está diseñado para mejorar la precisión de la clasificación de imágenes y la eficacia general del sistema. La eficacia del sistema propuesto se evalúa mediante el análisis de métricas de rendimiento clave, como la puntuación F1, la precisión, la exactitud y la recuperación.

Palabras clave: Clasificación de Imágenes; Computación Cuántica; Red Neuronal Convolucional; Ajustes de Peso; Moda MNIST.

INTRODUCTION

Classifying multi-class fashion products poses a formidable challenge necessitating differentiation among various classes. The classification task is beset by numerous challenges, including variability in noise, variations in lighting conditions, susceptibility to distortion, and inherent similarities between certain objects. While various methods for fashion image classification have been employed, they often encounter misclassification issues. Deep Learning (DL) algorithms, as exemplified by neural networks (NN), offer promising solutions by directly learning essential image features or attributes from the data.⁽¹⁾ Although artificial neural networks (ANN) have been used for image classification, they fall short in accounting for the spatial structure of images, treating each pixel as an independent feature, which results in suboptimal performance.⁽²⁾ To address this spatial structure issue, Convolutional Neural Networks (CNN) have emerged, comprising convolutional layers for feature learning, pooling layers for down sampling, and fully connected layers for the final classification process.^(3,4,5) CNNs share similarities with traditional NNs, featuring hidden layers with trainable parameters in each node. These nodes process inputs through dot products and subsequent non-linear transformations, effectively mapping raw image pixels to corresponding class scores. Notably, while ANN converts 2D images into 1D vectors before training, CNNs excel in 2D image classification, offering superior accuracy.

In the realm of quantum computing, there exists the potential to surpass classical computers, particularly in enhancing feature extraction and state approximation. Quantum bits (qubits) harness superposition, enabling them to exist in two states simultaneously (e.g., 0 and 1). Quantum Computing (QC) exploits adjacent pairs of qubits for computation. Quantum Convolutional Neural Networks (QCNN)⁽⁶⁾ leverage variational parameters to make quantum systems trainable, demonstrating proficiency in addressing significant challenges like quantum phase recognition and quantum error correction, thereby enhancing feasibility.

Recent advancements have witnessed the implementation of numerous Machine Learning (ML) and Deep Learning (DL) algorithms for fashion product image classification. Quantum image classification offers distinct advantages, including reduced space complexity, faster runtime, and fewer qubits required for image encoding. Consequently, gate-based quantum state vectors and quantum simulators⁽⁷⁾ have been employed to improve training on large datasets by dividing the data into smaller subsets, although noise from quantum devices has introduced precision and classification challenges. An extension of Quantum Neural Networks (QNN)⁽⁸⁾, aims to enhance image encoding and train Quantum Convolutional Neural Networks (QCNN), incorporating encoding, trainable quanvolutional layers, classical NN layers, and classical post-processing and optimization. Around 120 experiments have been conducted, exploring various combinations of encoding approaches, quanvolutional filter sizes, strides, and rotations in variational circuits.⁽⁹⁾ QCNN applies convolutional and pooling layers similar to CNN in quantum systems. The learnability of QNN⁽¹⁰⁾ is characterized by its inherent unpredictability due to gate noise, measurement error, and non-convex optimization landscapes. Therefore, this study investigates QNN’s learnability, focusing on generalization and trainability, while utilizing statistical learning and optimization techniques. Performance comparisons encompass high-order gradient descent methods, loss functions, and optimizers. Despite the achievements of existing methods in fashion product image classification, they still encounter challenges in precise image prediction and identification.

To address misclassification issues, we propose the Dual-Resolution Quantum Convolutional Neural Network (DRQCNN) featuring two levels of weight adjustment mechanisms. We employ the Fashion MNIST dataset containing various apparel classes, preprocess the images to optimize quality, and perform train-test data splitting. The trained images are subsequently employed for classification, with quantum computing mechanisms implemented alongside Deep Convolutional Neural Networks (DCNN) to enhance image manipulation and representation. The DRQCNN incorporates convolutional layers for feature extraction, pooling layers for dimension reduction, and dense layers for classification. Batch normalization is applied to stabilize and expedite the network. The dense layer classifies images based on the output of previous layers. In parallel, the proposed system’s performance is compared with traditional ANN. Subsequently, the classified model undergoes a prediction phase to evaluate the efficiency of trained data with test data. Performance evaluation metrics include F1-score, precision, accuracy, and recall.

The primary contributions of this paper are summarized as follows:

· The utilization of a quantum-based CNN with a weight adjustment strategy for fashion MNIST dataset classification.

· Improved classification accuracy and enhanced reliability achieved by comparing the performance of DRQCNN with the traditional ANN algorithm.

· Evaluation of the proposed system’s efficiency using performance metrics, including F1-score, precision, accuracy, and recall.

Paper Organization

The paper is structured to provide a coherent and logical flow of information, beginning with the elucidation of key concepts pertaining to quantum CNN based image classification for the Fashion MNIST dataset. Following this foundational discussion, Section II delves into an in-depth analysis of traditional approaches. Moving forward, Section III presents the proposed system, encompassing its workflow and algorithms. This section explains the intricate details of the system architecture, ensuring a comprehensive understanding of its inner workings. In Section IV, the paper presents the results obtained from the application of the proposed system. Furthermore, it conducts a comparative study, contrasting the performance of the proposed system with existing methods. This section serves to provide empirical evidence of the system’s efficacy and its potential to outperform conventional approaches. Lastly, Section V serves as the culmination of the paper, where conclusions drawn from the study are presented. Additionally, the paper outlines avenues for future research, thereby contributing to the ongoing advancement of the field. This structured organization ensures a systematic and coherent presentation of the research, facilitating a clear understanding of the contributions and implications of the study.

Literature Review

This section undertakes a comprehensive examination and appraisal of diverse techniques pertinent to image classification in the context of the Fashion MNIST dataset, coupled with the identification of associated challenges. One notable approach featured herein is the implementation of a fully parameterized QCNN tailored for classical data classification, primarily leveraging two-qubit interactions. Within this paradigm, the QCNN architecture, as delineated Hur et al.⁽¹¹⁾ is thoughtfully combined with various factors, including the structural configuration of parameterized QC for optimization, preprocessing of classical data, cost functions, and quantum data encoding methods. Furthermore, this methodology incorporates convolutional kernels and pooling operators. An augmentation to the utility of QCNN is achieved through the utilization of distinct data encoding techniques, specifically hybrid angle encoding and hybrid direct encoding, accompanied by dynamic adjustments in QC depth and width. Notably, this approach yields an impressive accuracy rate of 94 % when applied to the Fashion MNIST dataset.

Additionally, Shen et al.⁽¹²⁾ explores the application of transfer learning  as a strategic tool to address the manifold challenges encountered during the training of accurate CNNs. The concept of fine-tuning emerges as a pivotal mechanism for mitigating the challenges associated with limited training data and the costly process of labelling new data instances. In this context, a flexible multi-tuning method is deployed, complemented by a policy network, which efficiently determines the fine-tuning parameters for individual data samples. This policy network is also tasked with optimizing the weighting assigned to the various fine-tuning techniques. Furthermore, the section evaluates the impact of diverse feature descriptors and classifiers in the context of fashion product classification tasks, as expounded Greeshma et al.⁽¹³⁾. Specifically, the classification is carried out on the Fashion MNIST dataset employing two classifiers: CNN⁽¹⁴⁾ and Support Vector Machine (SVM). SVM leverages feature descriptors such as Local Binary Patterns (LBP) and Histograms of Oriented Gradients (HOG),⁽¹⁵⁾ resulting in a commendable accuracy rate of 91,59 %.

Recognizing the inherent challenges of multi-class classification, especially when dealing with closely related classes, Seo et al.⁽¹⁶⁾ delves into the application of Hierarchical CNN (H-CNN) for apparel classification. A pivotal step involves the pre-definition of hierarchical labels within the dataset through data-driven procedures. Prior to training the H-CNN, a base CNN module is trained independently, omitting the hierarchical classifiers. This approach yields a noteworthy accuracy rate of 93 %. Subsequently, Alotaibi⁽¹⁷⁾ introduces the framework of Deep Auto DNN for apparel classification, which entails a fusion of deep autoencoders and Deep Neural Networks (DNNs). This configuration serves to extract high-level features and composite patterns from fashion samples in a supervised manner. Computational time analysis reveals that the Deep Auto DNN framework is remarkably efficient, taking approximately 0,001 seconds per image. Furthermore, increasing the number of hidden layers within the NN leads to enhanced framework performance, culminating in a precision rate of 93,365 %.

In the realm of QC, Easom-McCaldin et al.⁽¹⁸⁾ explores the deployment of a single-qubit-based Deep Quantum Neural Network (DQNN) as an innovative approach to image classification, emphasizing a reduction in the number of parameters compared to conventional techniques. This model undergoes rigorous evaluation across various datasets, including ORL, Fashion MNIST, and MNIST, in a Noisy Intermediate Scale Quantum (NISQ) environment. Notably, the DQNN demonstrates superior classification accuracy, despite the influence of qubit decay due to amplitude damping.⁽¹⁹⁾

In addition to conventional neural network models, Sun et al.⁽¹⁹⁾ highlights the utility of Quantum Superposition Spiking Neural Network (QS-SNN) as a means to enhance robustness within the system. QS-SNN leverages quantum superposition and quantum image encoding states for information representation, subsequently subjecting this information to processing through spatial-temporal SNN mechanisms. Comparatively, this approach outperforms traditional ANN methods in image recognition tasks.

Furthermore, Greeshma et al.⁽²⁰⁾ acknowledges the rapid advancements facilitated by Convolutional Neural Networks (CNNs) in image classification. A variant of CNN, specifically a DCNN with data augmentation, is introduced. This DCNN configuration is augmented with various regularization techniques and Hyper Parameter Optimization (HPO), applied to the Fashion MNIST dataset. To address the challenge of limited image samples required for DL, diverse data augmentation techniques such as shifting, rotation, cropping, and flipping are employed. Consequently, the model attains an impressive precision rate of 93,99 %.

A hybrid approach known as Quantum Dilated CNN (QDCNN)⁽²¹⁾ is introduced to capture large contextual information while executing quantum convolution processes, effectively mitigating computational costs. Evaluation results on Fashion MNIST and MNIST datasets showcase classification accuracy rates of 80,5 % and 89,5 %, respectively.

Furthermore, explores the implementation of a quantum-alternative Artificial Neural Network (ANN) for image classification. The proposed system constructs and tests a combination of traditional NN and QC elements to ensure optimal performance. Remarkably, this approach minimizes computational resources by employing simple quantum gates within a Variational Quantum Circuit (VQC).⁽²²⁾ These low-parameter quantum gates substantially reduce power consumption, leading to enhanced efficiency. By initializing and updating rotational gates during training, the system effectively optimizes the cost function, thereby establishing a clear relationship between performance and the number of parameters.

Additionally, a Quantum-Enhanced ML algorithm introduced by Sahoo et al.⁽²³⁾, grounded in a shallow variational ansatz, is deployed for image classification on the Fashion MNIST dataset. The system addresses challenges related to quantum phase recognition for specific spin models and employs error mitigation techniques to assess its performance.

In the context of CNNs, Henderson et al.⁽²⁴⁾ underscores the use of quanvolutional layers, which transform input data analogously to random convolutional filter layers. These transformations yield valuable attributes for image recognition, with the distinct advantage of requiring smaller quantum circuits and reduced error correction. The efficacy of quantum transformations is demonstrated by comparing different models across the MNIST dataset, including QNN, CNN, and CNN with additional non-linearities. This approach yields a notable accuracy rate of 95 %, surpassing traditional CNNs in terms of training efficiency.

Moreover, Caro et al.⁽²⁵⁾ introduce the concept of angle encoding with learnable rotation, which effectively reduces the number of qubits and circuit depth. Quantum convolutional layers, implemented with multiple quantum circuits, are subjected to an evaluation of parameters such as dilation, stride, and arbitrary size. This approach enables the learning of multiple feature maps with a single quantum circuit through the utilization of encoding with learnable rotation, ultimately resulting in reduced computational costs and improved precision.

Finally, Konar et al.⁽²⁶⁾ explores the Random Neural Network (RNN) with a hybrid classical-quantum methodology, incorporating amplitude encoding features and superposition states. The overarching goal is to utilize qubits to achieve robust classification in noisy environments, thereby enhancing accuracy. The quantum information is processed on qubits via various quantum gate procedures, while classical layers rely on random spiking neural networks. This framework is evaluated across multiple datasets, including KMNIST, MNIST, and Fashion MNIST, yielding an impressive classification accuracy of 94,9 %.

Problem Identification

In this section, we delve into the principal concerns arising from the examination of conventional algorithms:

· The study employs an adaptive multi-tuning approach; however, it exhibits a deficiency in the employment of hyper-parameter distribution for the purpose of achieving efficient fine-tuning15.

· Utilizing a variational QNN, the research faces computational challenges in terms of inference on quantum simulators and learning. Additionally, it endeavors to emulate noisy quantum hardware, a pursuit that inevitably leads to a reduction in the overall accuracy of the framework19.

· Within the study, two classifiers, namely CNN) and SVM based on LBP and HOG, are employed for object classification within the Fashion MNIST dataset. Nevertheless, the model exhibits shortcomings in terms of optimizing efficiency and effectiveness8.

METHOD

Traditional DL methodologies exhibit shortcomings in optimization, reliability, and adaptability. In response to these limitations, our proposed system leverages QC as a means to efficiently process data within a classical intractable framework. This novel approach is embodied in the DRQCNN, an amalgamation of quantum computing and DCNN architecture, supplemented by a weight adjustment mechanism to enhance image classification accuracy. The evaluation of this system is conducted on the Fashion MNIST dataset, which comprises 60 000 training samples and 10 000 testing samples, each representing images of dimensions 28 pixels in width and 28 pixels in height, totalling 784 pixels. These images are grayscale and correspond to 10 distinct classes.

For the purpose of this classification task, we specifically focus on classes 5 (Sandals) and 7 (Sneaker). Our workflow begins with the dataset loading and image pre-processing stage, where noise removal and image quality enhancement are applied to facilitate more precise image analysis. Subsequently, the pre-processed images are segregated into training and testing subsets, with the training data exclusively employed for classification purposes. The classification process involves a comparative analysis between our proposed DRQCNN model and the conventional ANN algorithm, incorporating the DCNN with quantum computing and weight adjustment components.

Notably, the QCNN integrated within our system employs a kernel matrix with reduced dimensions compared to the input image size, resulting in a diminished parameter requirement. This, in turn, reduces computational complexity and augments system performance. The weights of the kernels are adjusted using backpropagation to minimize the disparity between predicted outputs and actual values. This adaptive mechanism enhances the ability of DRQCNN to learn more effective feature representations tailored to the specific classification task at hand. The overall process for image classification based on DRQCNN is illustrated in figure 1.

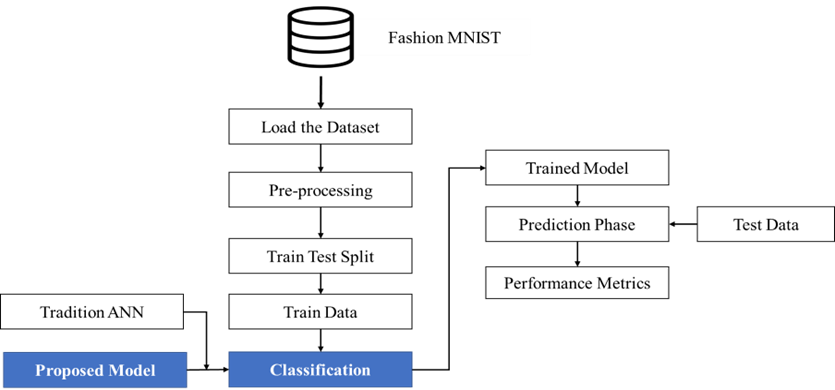
Figure 1. Overall Process of Image Classification Based on DRQCNN for Fashion MNIST Dataset

Batch normalization is strategically inserted between the maximum pooling layer and the dense layer within our network architecture. In this arrangement, the output emanating from the maximum pooling layer undergoes a standardization process via batch normalization before being forwarded as input to the subsequent dense layer. This judicious placement of batch normalization contributes to enhanced training speed and improved learning rates, resulting in a more efficient and effective training process.

Following the training phase, the classified images are juxtaposed with the test dataset to evaluate the performance of the trained DRQCNN algorithm. This assessment is based on several key performance metrics, including but not limited to the F1-score, precision, accuracy, and recall. These metrics collectively provide a comprehensive and quantifiable measure of the algorithm’s classification prowess, offering insights into its ability to correctly identify and classify images within the test dataset.

Traditional Artificial Neural Network (ANN)

ANNs are inspired by the structural and functional aspects of the human brain, with data processing and transfer occurring through multiple layers of interconnected neurons or nodes. Typically, ANNs consist of two primary layers: the input layer, serving as the initial point for data ingestion, and the output layer, positioned at the network’s apex, responsible for producing the final results in the form of a probability distribution across all potential classes.^(27,28) Between these layers, there exists an intermediate layer known as the hidden layer, which carries out intermediate computations and evaluations.

The training of ANNs hinges on the backpropagation approach, which involves iteratively adjusting the weights of connections among nodes within the network to minimize the loss function.^(29,30) This loss function quantifies the disparity between the model’s predicted output and the actual output. By calculating the gradients of the loss function with respect to the network’s weights, these gradients are subsequently employed to update the weights through the gradient descent optimization technique.

In the context of information flow, ANNs operate as feed-forward networks, meaning that data moves from one layer to another without circulating through a node more than once. This layered architecture empowers neural networks to comprehend and acquire knowledge pertaining to intricate patterns and relationships within data. ANNs find utility in various image-related tasks, encompassing image segmentation, data reduction, and preprocessing. However, ANNs are not without their limitations. They often exhibit a fuzzy architecture, making it challenging to elucidate their inner workings. Training neural networks can be a formidable task, often demanding copious amounts of data for effective model convergence. Additionally, when working with two-dimensional images, they must be converted into one-dimensional vectors, which can dramatically increase the number of trainable parameters and computational demands. To mitigate these challenges, the presented algorithm outlines specific steps in the training process aimed at minimizing the likelihood of suboptimal ANN convergence

Algorithm I: Traditional ANN (Artificial Neural Network)

Step I: Initialization

Set the weights (w) to random numbers.

Step II: Forward Propagation

Propagate the input neuron values (x) through hidden neurons to the output neuron.

Evaluate the output neuron values (ANN probabilities).

Evaluate the error function using equation (A1).

Step III: Backward Propagation

Calculate the gradient (g) for the network neurons.

Update the weights (w) using the gradient.

Increase the iteration count (p) by one.

Repeat steps 2 and 3 until the selected error criterion is satisfied.

Step IV: Repeat (recommended)

Repeat the entire process starting from step 1 to minimize the probability of ending up with a sub-optimal ANN.

Quantum Convolutional Neural Network (DRQCNN)

QC employs quantum bits, or qubits, in contrast to classical bits, and harnesses their unique properties such as uncertainty, superposition, and entanglement. In contrast, the DRQCNN possesses the innate capability to autonomously acquire spatial hierarchies of features critical for image recognition. This network structure comprises a sequence of interconnected layers designed to process input data. Within each layer, a 2D array of pixels, referred to as a feature map, is derived from the preceding layer. These layers encompass the convolutional layer, pooling layer, and fully connected layers. The pivotal component of the DRQCNN is the 2D convolutional layer, which plays a central role in encoding image data into a quantum system. The schematic representation of the quantum environment within the CNN, featuring level adjustments, is elucidated in figure 2.

Figure 2. Schematic Diagram of Quantum Environment in CNN with Level Adjustment

Multiple 2D matrices serve as input data for testing, and they yield multiple 2D matrices as output. Notably, the number of input matrices does not necessarily match the number of output matrices. Each set of kernel matrices functions as a local feature extractor, responsible for capturing regional features within the input matrices. Training the kernel matrices involves utilizing backpropagation to augment the connection weights within a neural network, thus acting as shared connection weights. Subsequently, a pooling layer is employed to reduce the dimensionality of images by merging neighboring elements within the convolution output matrices. Two commonly used pooling algorithms are max-pooling and avg-pooling. In the proposed method, a max-pooling layer is utilized, selecting the highest value among neighboring elements of the input matrix to generate a corresponding element in the output matrix. This process results in a reduction of feature map dimensions, while considering the minimum significant information from adjacent pixels.

In the quantum domain, quantum gates, represented as unitary matrices, induce transformations on quantum states. These quantum states are characterized by qubits, each capable of assuming values of 0 or 1, with probabilities determined by the square of the corresponding amplitude. This phenomenon is expressed as:

Here, |G) represents the garbage state, and the amplitude estimation of any positive integer is determined by:

Within unitary operations, there exists a mapping u:|0^⊗n)→ √alg |x,1)+√(1-alg) |G,0) for ½<alg<1. subsequently, a quantum algorithm is introduced, characterized by △>0 and 1⁄2<alg₀<alg, which produces a state such that 2T[(ln(1/△)/(2(|alg₀|-1^2/2)]. These subroutines are essential for encoding vectors into quantum states. Optimization of the fully connected function and weights is achieved through training on extensive datasets.

Consider a single kernel within the context of R^{I^l×W^l×Dim^l}. This kernel traverses various regions of the input and produces outputs for each region. Specifically, the input consists of a3D tensor input, A^l ∈ R^{I^l ×W^l×Dim^l} and 4d Tensor, Q^l∈R^{I×W×Dim^l×Dim^(l+1)}. Quantum states are generated, approximating |f(A^l+1), where A^l+1=A^l*Q^l and f: R→[0,C]. The classical approximation of this quantum process is expressed as:

The time complexity of this procedure is O (M/∈), where M represents the maximum norm of a product between Dim^l+1 kernel and A^l of size IWDim^l. The complexity is further influenced by factors that diminish poly-logarithmically in ∆, the size of A^l and Q^l. The output constitutes the quantum state representation of the convolution product, facilitating the transfer of information from the previous layer to the next. Pixels with lower values in the output indicate the absence of patterns in the corresponding input regions. Figure 3 illustrates the layered structure of DRQCNN.

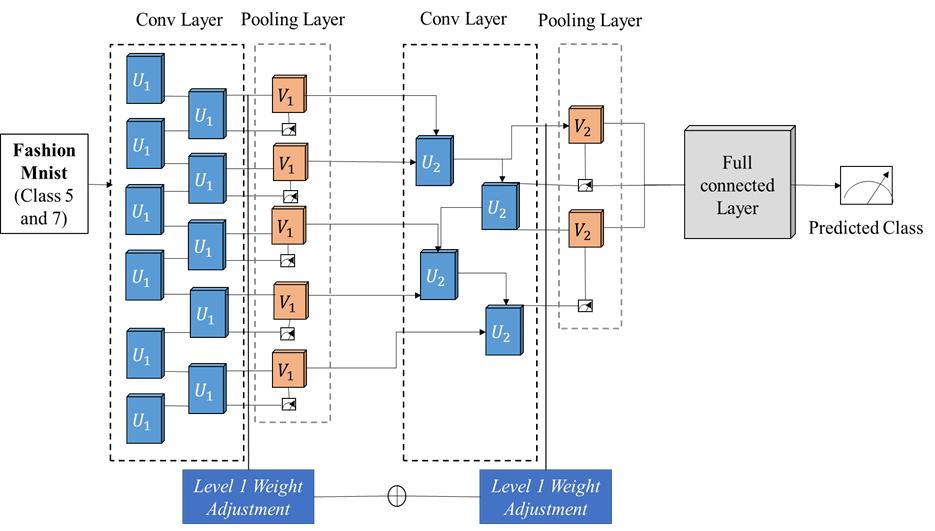
Figure 3. Paradigm of DRQCNN with Layered Structure

The figure illustrates the layered architecture of the system, with Fashion MNIST images (specifically, classes 5 and 7) represented as quantum states serving as the input. Within this architecture, a convolutional layer applies a single quasilocal unitary transformation, denoted as U1, in a translationally consistent manner throughout predictable depth. During pooling operations, a fraction of qubits undergo evaluation, and the corresponding effects modulate unitary rotations represented as V1. These rotations are applied to neighboring qubits, introducing non-linearity into the DRQCNN by reducing the degrees of freedom. Both convolutional and pooling layers are processed until the model’s dimensions become sufficiently small. In contrast, the fully connected layer is implemented as a unitary transformation applied to the residual qubits. Consequently, the system’s output is generated by computing a fixed number of output qubits, with weights added at each convolutional layer. Notably, DRQCNN hyperparameters, such as the number of convolution and pooling layers, remain static, while unitaries are learned autonomously.

The input consists of two key components: the data kernel matrix Kerl and the input matrix Al, both retained within DRQCNN. A non-linearity function, denoted as f: R→[0,C], is employed, alongside precision attributes denoted as ∈ and η. The output, denoted as B^l+1, corresponds to the data matrix resulting from convolution between the input and weight matrices, followed by pooling and non-linear transformations.

Step 1: QC

Inner Product Estimation: To achieve QCNN-based mapping, the following computation is performed:

Where:

K represents the normalization factor.

Non-linearity: two QCNNs and an arithmetic circuit are employed to compute the convolution output while applying the non-linear function:

Step 2: Weight Adjustment

Both weight adjustment and conditional rotation are applied to obtain the state as follows:

The values with high probability (pol,Quat ,f(Y ̅_pol,Quat^l+i) above the precision  are retained, while the others are set to 0.

Step 3: QCNN Update

The QCNN is updated to sample for the subsequent layer, B^l+1. Both average and maximum pooling operations are performed as part of the QCNN update.

The hyperparameters derived from DRQCNN include:

· Number of convolution and pooling layers, which remain static.

· Parameters related to unitary transformations, which are autonomously learned within the system.

Quantum Pooling Layer

The primary purpose of the pooling layer is to reduce spatial dimensions and decrease the number of parameters. In the case of 2x2 pixel pooling, an operation is performed with a stride of 2 pixels. The input image is denoted as:

Here, |g’ represents the final image from the previous layer, obtained by feature extraction from the input image. The output after performing quantum pooling is represented as:

Where |p is the final image extracted from the quantum pooling layer.

Quantum Fully Connected Layer

The fully connected layer typically serves as the final stage of a Convolutional Neural Network (CNN), consolidating data from previous layers to produce the final output. In this context, a parameterized Hamiltonian is introduced as a second-order link, forming the quantum fully connected layer, as given by equation (9):

Here, h⁰, hⁱ, h^ij are parameters, and σ_zⁱ represents the Pauli matrix. This Hamiltonian consists of both Pauli and identity operators, where the Pauli matrix acts on qubits at specific sites.

The Hamiltonian’s expectation value, f(pol)=(pol|I|pol), is measured, and the features of the Hamiltonian matrix are optimized using gradient descent, as expressed in equation (10).

Gradient Descent Method:

The cost function is redefined as follows:

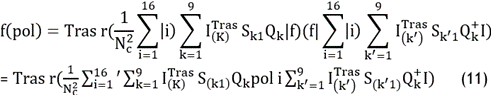
Here, pol i=|f)|i)(i|f|. From equation (8), the partial derivative of the cost function is given by:

The parameters are updated by computing the probability values of specific operators. This approach enhances the proposed DRQCNN system by employing quantum pooling, weight adjustment mechanisms, and a reduced parameter count, resulting in improved performance and significant results, particularly for large datasets.

RESULTS AND DISCUSSION

This section provides a detailed discussion of the results obtained from the various mechanisms implemented in the system. Additionally, it includes a description of the dataset used, exploratory data analysis (EDA), performance metrics, experimental findings, and a comparative analysis of existing techniques.

Dataset Description

The system utilizes the Fashion MNIST dataset, which comprises 60 000 images in the training set and 10 000 images in the test set, distributed across 10 classes. These classes are as follows:

· T-shirt/top.

· Trouser.

· Pullover.

· Dress.

· Coat.

· Sandal.

· Shirt.

· Sneaker.

· Bag.

· Ankle Boot.

Each class contains 7000 images. However, for the classification task, the system focuses solely on two classes:

· Sandal.

· Sneaker.

Exploratory Data Analysis (EDA)

EDA is a crucial step in understanding and summarizing the input data. It provides valuable insights, detects anomalies, checks assumptions, and identifies data patterns. Figure 4 depict sample plots derived from the Fashion MNIST dataset, facilitating a visual understanding of the data distribution and characteristics.

Figure 4. Sample Plot of Sandal

Figure 5 provides a visual representation of the dataset, showcasing images from Class 5 (Sandal) and Class 7 (Sneakers). This graphical representation aids in understanding the distinct characteristics of these two classes, which are crucial for the classification task.

In the parametrized quantum circuit, synchronized quantum operations are executed on quantum data while classical processing occurs simultaneously. Figure 6 illustrates the Scalable Vector Graphics (SVG) circuit employed within the proposed system. This circuit plays a pivotal role in enhancing the classification algorithm’s capabilities.

Figure 5. Sample plot of Sneaker

Figure 6. SVG Circuit

The integration of quantum operations and classical processing within the circuit exemplifies the system’s sophisticated approach to data classification, harnessing the capabilities of quantum computing to enhance overall results.

The SVG consists of 4 Hadamard structures, 7 rotational gates, and 6 entanglement gates, forming a complex quantum circuit. Within this circuit, multiple quantum gates, measurement circuits, and quantum variables are combined under specific conditions, as depicted in figure 7.

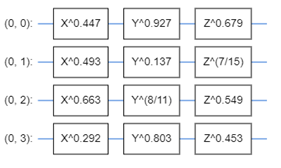
Figure 7. Parameterised Quantum Circuit

This parameterized quantum circuit is a critical component of the system, orchestrating the quantum operations that underpin the classification process. It produces a feature map across 8 channels, as illustrated in the figure. This feature map, in turn, plays a pivotal role in predicting classification results, working in conjunction with the fully connected layer to achieve accurate and meaningful outcomes.

Performance Analysis

The performance evaluation of the proposed method relies on several key metrics, including precision, accuracy, recall, and the F1-score. Here, we provide definitions and equations for each of these metrics:

Precision (P)

Precision measures the proportion of correctly predicted positive cases out of all cases that were predicted as positive. It is given by the equation (13):

Where Tp (True Positive) represents the number of correctly predicted positive cases, and Fp (False Positive) represents the number of cases incorrectly predicted as positive.

Accuracy (A)

Accuracy quantifies the overall correctness of the predictions and is defined as the ratio of correctly predicted instances (both positive and negative) to the total number of instances. It is given by the equation (14):

Where Tn (True Negative) is the number of correctly predicted negative cases, and Fn (False Negative) is the number of cases incorrectly predicted as negative.

Recall (R)

Recall, also known as sensitivity or true positive rate, assesses the proportion of correctly identified positive cases out of all actual positive cases. It is given by the equation (15):

Where Fn (False Negative) represents the number of actual positive cases that were incorrectly predicted as negative.

F1-score (F1)

The F1-score is a combined metric that balances precision and recall. It provides a harmonic mean of these two metrics, offering a single value that reflects the overall performance. It is calculated using the equation (16):

The F1-score is useful when there’s a need to balance precision and recall, especially when the data is imbalanced.

These metrics collectively support assess the effectiveness and robustness of the proposed method in solving the classification task, particularly in the context of classes 5 (Sandals) and 7 (Sneakers) in the Fashion MNIST dataset.

Experimental Results

The proposed system, implemented using DRQCNN, has yielded promising results, which are summarized in table 1 and visually represented in figure 8.

Table 1. Accuracy of the Proposed System
Model	Accuracy
Traditional ANN	46
Proposed	98,5

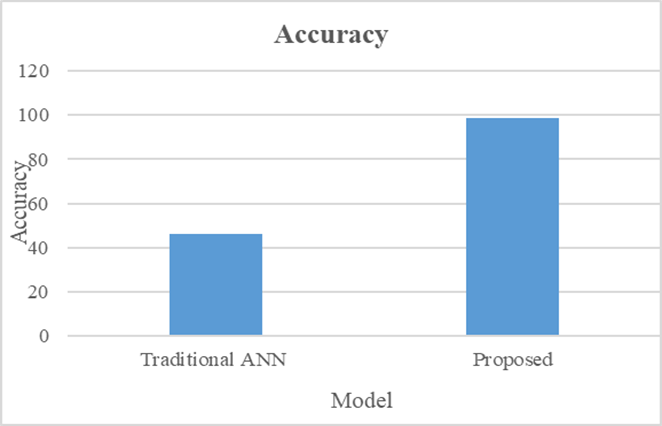
Figure 8. Graphical Representation of Comparison of ANN with DRQCNN

From figure 8, it is evident that a comparison between the proposed DRQCNN model and the traditional ANN has been conducted. The results clearly demonstrate that the proposed DRQCNN model outperforms traditional methods. While the traditional ANN approach achieved an accuracy rate of only 46 %, the proposed DRQCNN achieved an impressive accuracy rate of 98,5 %. Table 2 provides a more detailed breakdown of accuracy and loss metrics for both the traditional ANN and the proposed DRQCNN:

Table 2. Accuracy and Loss of Traditional ANN and Proposed Method
Models	Accuracy	Loss
Traditional ANN	46,00	6,62
Proposed	98,50	0,12

Accuracy, in this context, represents the proportion of correct classifications out of the total classifications made. These results clearly demonstrate the significant improvement achieved by the proposed DRQCNN over the traditional ANN in terms of both accuracy and loss.

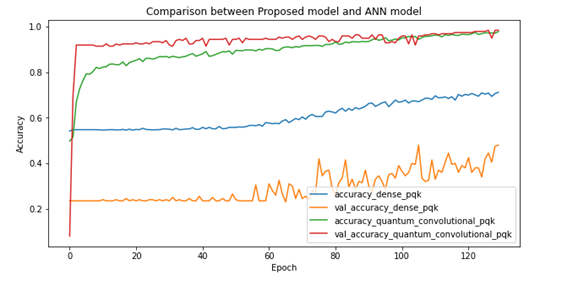
Figure 9. Accuracy Prediction with Corresponding Epochs

Figure 9 illustrates the model’s accuracy and validation accuracy across different numbers of epochs. Notably, the accuracy and validation accuracy of DRQCNN in Fashion MNIST image classification of two classes consistently remain high, reaching an impressive accuracy rate of 98,5 %. This further emphasizes the robust performance of the proposed DRQCNN model.

Comparative Analysis

The binary classification of the Fashion MNIST dataset, specifically classes 5 and 7, presents a more challenging task compared to binary classification in the standard MNIST dataset. The study outlined here adopts a hybrid approach, combining quantum-inspired tensor networks and VQC for supervised learning. This hybrid model enables simultaneous training of both quantum and classical sections, offering flexibility and the potential for implementation on quantum hardware.

In this study, ternary classification is performed on the MNIST dataset, while both ternary and binary classifications are carried out on the Fashion MNIST dataset. The results are summarized in table 3, and a graphical representation is provided in figure 10.

Table 3. Accuracy of Existing Method10
Model	Accuracy
Existing model	96
Proposed	98,5

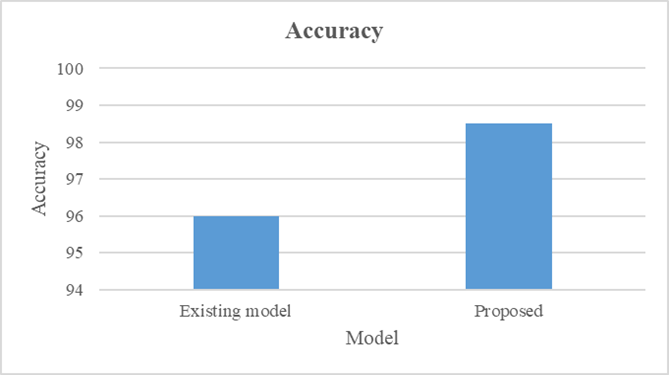
Figure 10. Graphical Representation of accuracy of existing and proposed model 10

Figure 10 illustrates the comparison of accuracy between the existing hybrid model and the proposed DRQCNN model. The existing hybrid model achieved an accuracy of 96 %, whereas the proposed DRQCNN achieved a significantly higher accuracy of 98,5 %. This indicates that the proposed model performs exceptionally well and offers superior efficiency compared to conventional algorithms.

It’s important to note that previous studies often focused on classifying all 10 classes within the Fashion MNIST dataset. However, only a few studies attempted binary classification of two distinct classes, which typically resulted in lower precision due to the inherent challenges. The classification of two different classes in Fashion MNIST has lower chances of success. Therefore, the proposed model takes a focused approach by classifying only two classes, namely 5 (Sandal) and 7 (Sneaker), using DRQCNN to achieve optimal results.

In contrast to traditional ANNs, which tend to increase the number of trainable parameters and subsequently raise storage and computational costs, QCNNs leverage quantum systems to enhance image classification. The incorporation of DRQCNN, coupled with a weight-sharing mechanism, optimizes dataset classification with superior precision. This highlights the potential of quantum-inspired models in advancing the field of image classification and machine learning.

CONCLUSIONS

QCNNs have proven to be well-suited for enhancing various processes such as time series analysis, signal processing, and visual recognition. Unlike some other CNN models, QCNNs excel in terms of generalization and mitigating overfitting. Additionally, QCNNs often result in fewer trainable parameters, thereby reducing computational costs and processing time. In this context, the proposed DRQCNN model, along with its weight adjustment mechanism, was developed to improve the learning capabilities of the framework, particularly for the Fashion MNIST dataset. The primary objective was to achieve accurate classification of classes, with a specific focus on classes 5 (Sandals) and 7 (Sneakers). The integration of QCNN played a pivotal role in enhancing image recognition and classification. The performance of the proposed system was assessed using key metrics such as F1-score, precision, accuracy, and recall. The experimental results demonstrated an impressive accuracy rate of 98,55 % when compared to the traditional ANN method. This clearly indicates that the proposed mechanism outperformed conventional methods in terms of classification accuracy. In future work, the extension of this approach to include other classes within the Fashion MNIST dataset could further improve classification performance. Additionally, the exploration of various other DL algorithms and techniques may offer opportunities to achieve even higher accuracy and reliability in image classification tasks. This study highlights the potential of quantum-inspired models in advancing the field of image classification and machine learning, opening the door for further research and innovation.

ACKNOWLEDGMENT

We thank the Deanship of Scientific Research, Prince Sattam Bin Abdulaziz University, Alkharj, Saudi Arabia for help and support. This study is supported via funding from Prince Sattam Bin Abdulaziz University project number (PSAU/2024/R/1445).

BIBLIOGRAPHIC REFERENCES

1. Vijayaraj A, Vasanth Raj PT, Jebakumar R, Gururama Senthilvel P, Kumar N, Suresh Kumar R, et al. Deep learning image classification for fashion design. Wirel Commun Mob Comput. 2022;2022(1):7549397.

2. Whig V, Othman B, Gehlot A, Haque MA, Qamar S, Singh J. An Empirical Analysis of Artificial Intelligence (AI) as a Growth Engine for the Healthcare Sector. In: 2022 2nd International Conference on Advance Computing and Innovative Technologies in Engineering (ICACITE). IEEE; 2022. p. 2454–7.

3. Chen Z, Lv M, Tian S, Yin S. Fashion-MNIST Classification Based on CNN Image Recognition. Highlights Sci Eng Technol. 2023;34:196–202.

4. Kayed M, Anter A, Mohamed H. Classification of garments from fashion MNIST dataset using CNN LeNet-5 architecture. In: 2020 international conference on innovative trends in communication and computer engineering (ITCE). IEEE; 2020. p. 238–43.

5. Kadam SS, Adamuthe AC, Patil AB. CNN model for image classification on MNIST and fashion-MNIST dataset. J Sci Res. 2020;64(2):374–84.

6. Cong I, Choi S, Lukin MD. Quantum convolutional neural networks. Nat Phys. 2019;15(12):1273–8.

7. Du Y, Huang T, You S, Hsieh MH, Tao D. Quantum circuit architecture search for variational quantum algorithms. npj Quantum Inf. 2022;8(1):62.

8. Anand A, Lyu M, Baweja PS, Patil V. Quantum image processing. arXiv Prepr arXiv220301831. 2022;

9. Chen SYC, Huang CM, Hsing CW, Kao YJ. An end-to-end trainable hybrid classical-quantum classifier. Mach Learn Sci Technol. 2021;2(4):45021.

10. Qian Y, Wang X, Du Y, Wu X, Tao D. The dilemma of quantum neural networks. IEEE Trans Neural Networks Learn Syst. 2022;

11. Hur T, Kim L, Park DK. Quantum convolutional neural network for classical data classification. Quantum Mach Intell. 2022;4(1):3.

12. Shen X, Plested J, Caldwell S, Zhong Y, Gedeon T. AMF: Adaptable Weighting Fusion with Multiple Fine-tuning for Image Classification. arXiv Prepr arXiv220712944. 2022;

13. Greeshma K V, Gripsy JV. Image classification using HOG and LBP feature descriptors with SVM and CNN. Int J Eng Res Technol. 2020;8(4):1–4.

14. LEITHARDT V. Classifying garments from fashion-MNIST dataset through CNNs. Adv Sci Technol Eng Syst J. 2021;6(1):989–94.

15. Greeshma K V, Sreekumar K. Fashion-MNIST classification based on HOG feature descriptor using SVM. Int J Innov Technol Explor Eng. 2019;8(5):960–2.

16. Seo Y, Shin K shik. Hierarchical convolutional neural networks for fashion image classification. Expert Syst Appl. 2019;116:328–39.

17. Alotaibi A. A hybird framework based on autoencoder and deep neural networks for fashion image classification. Int J Adv Comput Sci Appl. 2020;11(12).

18. Easom-McCaldin P, Bouridane A, Belatreche A, Jiang R, Al-Maadeed S. Efficient quantum image classification using single qubit encoding. IEEE Trans Neural Networks Learn Syst. 2022;35(2):1472–86.

19. Sun Y, Zeng Y, Zhang T. Quantum superposition inspired spiking neural network. Iscience. 2021;24(8).

20. Greeshma K V, Sreekumar K. Hyperparameter optimization and regularization on Fashion-MNIST classification. Int J Recent Technol Eng. 2019;8(2):3713–9.

21. Chen Y. QDCNN: Quantum Dilated Convolutional Neural Network. arXiv Prepr arXiv211015667. 2021;

22. Gil Fuster EM. Variational quantum classifier. 2019;

23. Sahoo S, Azad U, Singh H. Quantum phase recognition using quantum tensor networks. Eur Phys J Plus. 2022;137(12):1373.

24. Henderson M, Shakya S, Pradhan S, Cook T. Quanvolutional neural networks: powering image recognition with quantum circuits. Quantum Mach Intell. 2020;2(1):2.

25. Caro MC, Gil-Fuster E, Meyer JJ, Eisert J, Sweke R. Encoding-dependent generalization bounds for parametrized quantum circuits. Quantum. 2021;5:582.

26. Konar D, Gelenbe E, Bhandary S, Sarma A Das, Cangi A. Random quantum neural networks (RQNN) for noisy image recognition. arXiv Prepr arXiv220301764. 2022;

27. Haque MA, Ahmad S, Haque S, Kumar K, Mishra K, Mishra BK. Analyzing University Students’ Awareness of Cybersecurity. In: 2023 International Conference on Emerging Trends in Networks and Computer Communications (ETNCC). IEEE; 2023. p. 250–7.

28. Zeba S, Haque MA, Alhazmi S, Haque S. Advanced Topics in Machine Learning. Mach Learn Methods Eng Appl Dev. 2022;197.

29. Haque MA, Ahmad S, Sonal D, Abdeljaber HAM, Mishra BK, Eljialy AEM, et al. Achieving Organizational Effectiveness through Machine Learning Based Approaches for Malware Analysis and Detection. Data Metadata. 2023;2:139.

30. Hossain MA, Haque MA, Ahmad S, Abdeljaber HAM, Eljialy AEM, Alanazi A, et al. AI-enabled approach for enhancing obfuscated malware detection: a hybrid ensemble learning with combined feature selection techniques. Int J Syst Assur Eng Manag [Internet]. 2024; Available from: https://doi.org/10.1007/s13198-024-02294-y

FINANCING

This study is supported via funding from Prince Sattam Bin Abdulaziz University project number (PSAU/2024/R/1445).

CONFLICT OF INTEREST

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

AUTHORSHIP CONTRIBUTION

Conceptualization: Meshal Alharbi, Sultan Ahmad.

Investigation: Meshal Alharbi, Sultan Ahmad.

Methodology: Meshal Alharbi, Sultan Ahmad.                 

Writing - original draft: Meshal Alharbi, Sultan Ahmad.                    

Writing - review and editing: Meshal Alharbi, Sultan Ahmad.