doi: 10.56294/dm2024.365

ORIGINAL

Cluster Heat Selection Optimization in WSN Via Genetic Based Evolutionary Algorithm and Secure Data Transmission Using Paillier Homomorphic Cryptosystem

Optimización de la Selección de Calor de Cluster en WSN Mediante Algoritmo Evolutivo Basado en Genética y Transmisión Segura de Datos Utilizando el Criptosistema Homomórfico de Paillier

Yuvaraja M¹ *, Priya R² *, Uma Maheswari S³ *, Dhanasekar J⁴ *

¹Associate professor, Department of ECE, P. A. College of Engineering and Technology. Pollachi, Tamil Nadu, India.

²Assistant Professor, CSE, Pollachi Institute of Engineering and Technology. Pollachi, Coimbatore District, Tamila Nadu, India.

³Assistant Professor, Division of Data Science and Cyber Security, Karunya Institute of Technology and Sciences. Karunya Nagar, Coimbatore, Tamil Nadu.

⁴Assistant Professor, Department of ECE, Sri Eshwar College of Engineering. Coimbatore, Tamil Nadu, India.

Cite as: M Y, R P, S UM, J D. Cluster Heat Selection Optimization in WSN Via Genetic Based Evolutionary Algorithm and Secure Data Transmission Using Paillier Homomorphic Cryptosystem. Data and Metadata. 2024; 3:.365. https://doi.org/10.56294/dm2024.365

Submitted: 25-01-2024                   Revised: 19-04-2024                   Accepted: 02-09-2024                 Published: 03-09-2024

Editor: Adrián Alejandro Vitón Castillo

Corresponding Author:  Yuvaraja M *

ABSTRACT

Introduction: wireless Sensor Networks (WSNs) consist of sensor nodes requiring energy-saving measures to extend their lifespan. Traditional solutions often lead to premature node failure due to non-adaptive network setups. Differential Evolution (DE) and Genetic Algorithms (GA) are two key evolutionary algorithms used for optimizing cluster head (CH) selection in WSNs to enhance energy efficiency and prolong network lifetime.

Method: this study compares DE and GA for CH selection optimization, focusing on energy efficiency and network lifespan. It also introduces an improved decryption method for the Paillier homomorphic encryption system to reduce decryption time and computational cost.

Results: experiments show GA outperforms DE in the number of rounds for the first node to die (FND) and achieves a longer network lifespan, despite fewer rounds for the last node to die (LND). GA has slower fitness convergence but higher population fitness values and significantly faster decoding speeds.

Conclusions: GA is more effective than DE for CH selection in WSNs, leading to an extended network lifespan and better energy efficiency. Despite slower fitness convergence, GA’s higher fitness values and improved decoding speeds make it a superior choice. The enhancements to the Paillier encryption system further increase its efficiency, offering a robust solution for secure and efficient WSN operation.

Keywords: Wireless Sensor Network (WSN); Genetic Algorithm (GA); Differential Evolution (DE); Paillier Homomorphic Encryption (PHE).

RESUMEN

Introducción: las redes de sensores inalámbricos (WSN) consisten en nodos de sensores que requieren medidas de ahorro de energía para extender su vida útil. Las soluciones tradicionales a menudo provocan fallos prematuros en los nodos debido a configuraciones de red no adaptables. La evolución diferencial (DE) y los algoritmos genéticos (GA) son dos algoritmos evolutivos clave que se utilizan para optimizar la selección de cabezas de clúster (CH) en WSN para mejorar la eficiencia energética y prolongar la vida útil de la red.

Método: este estudio compara DE y GA para la optimización de la selección de CH, centrándose en la eficiencia energética y la vida útil de la red. También introduce un método de descifrado mejorado para el sistema de cifrado homomórfico de Paillier para reducir el tiempo de descifrado y el costo computacional.

Resultados: los experimentos muestran que GA supera a DE en el número de rondas para que muera el primer nodo (FND) y logra una vida útil de red más larga, a pesar de tener menos rondas para que muera el último nodo (LND). GA tiene una convergencia de aptitud más lenta pero valores de aptitud de la población más altos y velocidades de decodificación significativamente más rápidas.

Conclusiones: GA es más eficaz que DE para la selección de CH en WSN, lo que conduce a una vida útil de la red extendida y una mejor eficiencia energética. A pesar de una convergencia de aptitud más lenta, los valores de aptitud más altos de GA y las velocidades de decodificación mejoradas lo convierten en una opción superior. Las mejoras al sistema de cifrado Paillier aumentan aún más su eficiencia, ofreciendo una solución sólida para una operación WSN segura y eficiente.

Palabras clave: Red de Sensores Inalámbricos (WSN); Algoritmo Genético (GA); Evolución Diferencial (DE); Cifrado Homomórfico de Paillier (PHE).

INTRODUCTION

WSNs have grown to become crucial components of many applications in the recent decade.⁽¹⁾ WSNs have gained the attention of researchers due to their widespread usages in commercial and consumer applications.⁽²⁾ One power management technique used in WSNs are clustering the networks with a cluster leader assigned to groups. The CH combines the data received from the nodes in the cluster before delivering it to the base station, as opposed to each node transmitting its own data straight to it.⁽³⁾

On the other hand, research has recently been heavily focused on the examination of data and information protection.⁽⁴⁾ To safeguard the privacy of data and personal information, several encryption techniques have been created. The integrity and confidentiality of data can be guaranteed by multiple systems, but none of them can facilitate processing on encrypted data.⁽⁵⁾ The non-adaptive network architecture caused by the lack of global knowledge during decision-making is a typical flaw in conventional routing systems. Without taking global information into account, randomised CH placement may result in unequal CH placement and an ineffective clustering network.

It enhances CH selection and boosts data transmission security level performance to address these problems. CH selection optimisations are crucial to improve energy efficiencies in WSNs. However, in order to accomplish successful optimisation, many criteria must be considered. In order to overcome this difficulty, evolutionary algorithms are crucial since they have the ability to adaptively solve complicated problems in polynomial time.⁽⁶⁾

Research indicate that genetically based evolutionary algorithms like DEs and GAs are suitable.to make the CH selection process more efficient. Despite having a slightly longer execution time, GAs has beaten PSO (Particle Swarm Optimisation) in terms of energy efficiency and fitness value.⁽⁷⁾ Any homomorphic encryption technique, such as the Paillier scheme, requires computationally intensive processes for encryption and decryption on portable devices. Therefore, an enhanced and quick encryption and decryption technique that supports handheld devices with constrained computing power is required. For secure data transmission, the faster and better decryption method for Paillier homomorphic encryption is suggested. According to the testing findings, it extends the network’s life, boosts packet delivery rates, cuts down on delays, and enhances secure data transmission.

Literature review

Dattatraya et al.⁽⁸⁾ proposed a new CH selection approach to improve energy efficiency and network longevity. A unique fitness-based FGF (firefly swarm and Drosophila optimisation algorithm), which combines GSO (firefly swarm optimisation) and FFOA (Drosophila optimisation algorithm), is also offered in this work to choose the best CH in WSN. The proposed FGF compares favourably with other ones already in use, such PSO, GA, ABC (Artificial Bee Colony), GSO, ALO (Antlion Optimisation), and CS (Cuckoo Search), in terms of live node analysis, energy analysis, and cost function. It outperforms the prior approach.), GAL-LF (Group Search Algorithm Using Levy Flight), FFOA, and GOA (Grasshopper Optimisation Algorithm).

Gong et al.⁽⁹⁾ suggested IMCPSO framework for better multi-objective clustering using PSO. To help PSO identify cluster solutions in continuous spaces, a novel particle model of the cluster issue was created in the study. Subsequently, Pareto set’s distributions were analysed. The analysis’ findings guided the processes of choosing leaders and keeping the algorithm from being trapped at local optimums. The method vastly increased the effectiveness of discovering clustering solutions while being experimented with 28 datasets and nine cutting-edge clustering algorithms. According to their evaluated ARI indices, their suggested method outperformed other methods.

Agrawal et al.⁽¹⁰⁾ combined fuzzy logics with harmony searches to increase the network’s lifespan. The hot spot issue was covered because the researchers used a strategy known as heterogeneous clustering to solve it. Heterogeneous clusters are produced by the suggested technique. By contrasting the suggested algorithm with other well-known heterogeneous clustering methods and harmonic search-based algorithms in various network topologies, its efficacy is proved. The suggested protocol produces higher performance in all environments. Compared to the many techniques that have been suggested so far, it increases the network’s longevity.

METHOD

Exploration and optimisation algorithms based on the concepts of natural evolution are known as genetically based evolutionary algorithms. The population of solutions are genetically based evolutionary algorithms which get iteratively updated, and possible solutions are chosen as parents create new children. The population ultimately finds ideal answers at the end of generations. Operator variations are used throughout the generation process to sift through the population of potential solutions in pursuit of the global optimum. GAs and DEs are two evolutionary algorithms based on genetics. Both algorithms feature operators with functionalities that are comparable. The arrangement of these operators is the primary distinction between GA and DE. The following diagram illustrates how GA and DE are formed.

GAs

GAs are search and optimisation algorithms based on the concepts of natural evolutions.^(11,12) Natural selection and the notion of the fittest are the foundations of GAs. The initial chromosomal population transforms into a population of superior chromosomes, and these chromosomes serve as the answer. Selection, crossover, mutation, and substitution are the agents of evolution. Together, these operators help the algorithm find the best answer to a given issue.

Selections

Selections are operators of parent selections to generate next generations. RWS (roulette wheel selections) are the simplest selection schemes in which chromosomes are mapped into consecutive segments similar to roulette wheels.⁽¹³⁾ The size of each segment is related to its fitness. Therefore, the probability of each chromosome being selected by the roulette wheel can be expressed by the formula (1). The higher the fitness value of a chromosome, the higher the probability that that chromosome will be selected. The pseudocode for the RWS algorithm is shown in algorithm 1.

Algorithm 1: Roulette Wheel Sampling Algorithm

Step 1: roulette wheel sampling methodology.

Step 2: begin the population.

Step 3: separate a population’s chromosomes into continuous chunks.

Step 4: generate random pointers.

Step 5: decide which chromosome best fits the pointer position.

Crossovers

Crossovers are operators analogous to biological crossovers. The most used crossover method, single-point crossover, chooses random crossing points to identify the locations of the genes to be swapped.⁽¹⁴⁾ Two children will be born if this genetic region is used for mating. However, there is just a predetermined possibility that the two parents will mate. The offspring will resemble the parents perfectly if there is no mating. Algorithm 2 displays the one-point crossover pseudocode.

Algorithm 2: One-Point Crossover Algorithm

Step 1: initialization of crossover probability in first phases of one-point crossover algorithm.

Step 2: select parents from the general population.

Step 3: if the crossing probability is determined at random.

a. Construct arbitrary intersections.

b. Complete the one-point intersection.

Step 4: else

c. Clone parents

Step 5: end if.

Mutations

Mutations are operators that keep population diversity intact. Premature convergence can happen if the likelihood of mutation is very low. However, if the mutation probability is too large, convergence may also be challenging. Consequently, we require an ideal mutation probability. Multifit flip mutation, which selects a random number of genes for mutation, is one of the most used mutation procedures.⁽¹⁵⁾ Bit-flipping is performed on the chosen genes with a predetermined mutation frequency. Algorithm 3 displays the multi-bit flip mutation algorithm’s pseudocode.

Algorithm 3: Multi-Bit Flip Mutation Algorithm

Step 1: initialise the mutation probability in the first phase.

Step 2: choose genes from the chromosomes of the progeny.

Step 3: for number of selected genes until maximum number of selected genes.

a. If randomly generated probability ≤ mutation probability.

i. Retain selected genes.

b. Else.

i. Retain selected genes.

c.  End if

Step 4: end for.

Replacements

A new population can be created using the operator substitution. In each GA cycle, breeding ends with this stage. A steady-state replacement method is improper parent replacement. A more suitable chromosome replaces the parental chromosome using this replacement method.⁽¹⁶⁾ Algorithm 4 displays the pseudocode for this method.

Algorithm 4: Weak Parent Replacement Algorithm

Step 1: if fitness of trail offspring chromosome >fitness of parent chromosome.

a. Replace parent chromosome with offspring chromosome.

Step 2: else.

a. Abandon the offspring chromosome

Step 3: end if

Differential evolution

Vectors are used as the solution representation in DEs, a stochastic optimisation technique.⁽¹⁷⁾ Selection, recombination, and mutation are the three fundamental components of DE. These operators act similarly to GA operators. Crossover and replacement roles are included in recombination and selection.

Mutations

The sampling procedure in procedure 5 is initially used by the mutation operator to choose four vectors from the population. It has three parameter vectors as well as a target vector. Equation is used to compute using the parameter vector. produce a donor vector (2).⁽¹⁸⁾ The weighted difference gets less as the population’s vectors converge as.

Where:

 first parameter vectors

 second parameter vectors

 third parameter vectors

F is the differential weight which is a constant between 0 and 2.

 is donor vector.

Algorithm 5: Vector Sampling Algorithm

Step 1: set population’s Initial values.

Step 2: map population vectors as continuous segments.

Step 3: randomly create four pointers.

Step 4: select four vectors whose fitness spans pointers’s positions.

Recombination

Recombination operator will generate a trial offspring vector by mixing bits from target and donor vectors. This operator is based on equation (3) and its pseudo code is given in algorithm 6.⁽¹⁹⁾

Where: u_j,i,G , V_j,i,G and x_j,i,Gare the bits of trial offspring, donor and target vectors respectively, Cr is the crossover probability, and j_rand is the number of bits that is chosen randomly between 1 and vector length to avoid an exact clone of target vector.

Algorithm 6: Recombination Algorithm

Step 1: initialize the crossover probability.

Step 2: for number of bits until vector length.

Step 3: if randomly generated probability ≤ crossover probability.

Step 4: else number of bits= randomly chosen number of bits.

a. Take the bit from donor vector.

Step 5: else if.

a. Take the bit from target vector.

Step 6: end if.

Step 7: end for.

Selection

Applying assembler survival principles are selection operators. Only if the experimental child vector has a superior match, as determined by equation (4)⁽²⁰⁾ does it take the place of the target vector. Algorithm 7 displays the selection algorithm’s pseudocode.

Where:  are the trial offspring and target vectors respectively.

Algorithm 7: Selection Algorithm

Step 1: if fitness of trail offspring vector > fitness of target vector.

a. Replace target vector with trail offspring vector.

Step 2: else.

a. Abandon the trail offspring vector.

Step 3: end if.

Paillier homomorphic encryption

Additive homomorphic public key encryption, also known as Paillier encryption, is often employed in the fields of third-party data processing and cryptographic signal processing. A similar arithmetic operation may be performed on the ciphertext right after encryption, and the outcome is the same as the outcome of the corresponding operation in the plaintext domain. This is its homomorphic quality.⁽²¹⁾ Its probabilistic characteristic ensures the semantic security of the ciphertext by allowing alternative ciphertexts to be generated from the same plaintext using various encryption techniques.⁽²²⁾ The following are the encryption and decryption mechanisms,

Key generation: choose two huge prime numbers at random, p and q, and then determine their product N, the least common multiple of p and q, and then randomly choose integers satisfying following conditions:

Among them, function L(u)=(u-1)⁄N and function gcd(.) are used to calculate the greatest common divisor of two numbers. Z_N² is the set of integers less than xϵZ* , while Z* _(N²₎ is the set of integers coprime with N² in Z_(N³₎. (N,g) are λ are public key and private key, respectively in equation (5).

Encryption process: a random integer rϵZ_i is selected. For any plaintext mϵZ_w, the corresponding ciphertext c is obtained by using public key (N,g) encryption:

Equation (6) of the Paillier encryption scheme states that if the same public key is used to encrypt both the ciphertext c and the plaintext r, the same plaintext will be obtained. It is possible to acquire distinct ciphertexts c for m, but not for m with the same ciphertext c. The semantic security of the ciphertext is ensured since the plaintext m can be obtained when the decryption is restored.

Decryption process: equation (7) uses the secret key n to decrypt the encrypted ciphertext c and produce the matching plaintext m.

CRT-Based Paillier Cryptosystem: several encryption techniques employ CRT to hasten the encrypting or decryption process. The Paillier-based decoding approach results in decoding overload, while our study focuses on enhancing the decoding process through modular operations.⁽²³⁾ The reader is directed to⁽²⁴⁾ learn more about CRT and Euler and Fermat’s little theorem in order to properly comprehend CRT and its use in Paillier encryption.

The CRT-based Paillier scheme has three algorithms, namely; key generation, encryption, and decryption. The key generation and encryption algorithms have been described in section two above. In this section, the decryption process is explicated since that is the process intend to improve the equation (8-9).

Applying the L function which is defined as L={x<n²|x=1 mod n} and for the two moduli p and q, which are the product of n.

Recall that from equation (10):

Let, equation (11):

From the equation (12):

Which are pre-computed.

Also, from the equation (13):

Applying the CRT, the equation (14):

Parameter Settings

On a two-dimensional network structure, base stations and sensor nodes are distributed. The x and y coordinates of each sensor node and BS are specified specifically while creating a network topology model. The Euclidean distance between two points can be used to calculate the distance parameter utilised in the radio model. The method below may be used to determine the Euclidean distance d between two sensor nodes if the first sensor node’s coordinates are (x1, y1) and the second sensor node’s coordinates are (x2, y2). It may be calculated using (15).

The table 1 and table 2 show the parameter settings of WSNs and genetic-based evolutionary algorithms respectively.

Table 1. Parameter setting of WSNs
Parameters	Values
Base station Coordinates	x= -80 m, y= -80 m
Sensor Node Counts	200
Network Dimensions	100 m×100 m
Initial Energies	0,05 J
Bit Numbers	1000 bits

Table 2. Parameter Setting of GAs and DEs
Parameters	Symbols	values
Generation Numbers	Gn	1000
Population Sizes	P	50
Crossover Probabilities	Cr	0,9
Mutation Probabilities	Mr	0,3
Differential Weights	F	2

RESULTS AND DISCUSSION

The network sizes used for experiments ranged from 500 to 3000 with 0,02 (m/s) search speeds. Average hop loss, average hop delivery ratio (PDR), average end-to-end latency, and average energy remaining at network half-life.⁽²²⁾

Packet delivery ratio

As illustrated in table 2, PDR is defined as the proportion of packets received to packets created at the source.⁽²³⁾ The PDR for this statement is (16).

Packet loss ratio

The counts of packets discarded during the communication period, as indicated in table 3, is defined by PLR. Equation (1)’s definition of PLR is that it is the proportion of lost packets to produced packets (17).

Average end to end delay

According to equation 18, AEED is the average amount of time needed to transport a packet from source to destination.⁽²⁴⁾ Table 4 displays this AEED, which also includes processing time, queue time, propagation delay, and transmission time.

Encryption time

This is the entire amount of time needed to finish encrypting all the data on the network in order to raise the security level and based on equation (19).

Enter AT for the amount of time needed to encrypt the data. A_B and A_S represent the start and finish times, respectively.

Key generation time

This is the amount of time the system needs to produce the key while the data is being transmitted across the network. This may be stated as follows (20):

Here, BT is used to represent the key generation time. Key creation starts at a point called B_start, and it ends at a point called B_end.

Decryption time

The length of time it takes for systems on the network to finish the decryption process is what is meant by this term. The evaluation is based on equation (21).

 The term “decoding time” is “CT.” The process’s start time is designated as C_start, while its conclusion time is designated as C_end.

Figure 1. Packet Delivery Ratio Results

The comparison of the GA-AOMDV, LEACH-GA, and GA-DE-PHE techniques in terms of PDR is shown in figure 1. When compared to the GA-AOMDV and LEACH-GA methods that are currently in use, the GA-DE-PHE technique is more effective in this case. By computing the trust value of nodes and communication by calculating the fitness function, the suggested method’s PDR is GA-DE-PHE.

Figure 2. Delay Results

The comparison of the GA-AOMDV, LEACH-GA, and GA-DE-PHE techniques in terms of latency is shown in figure 2. The GA-DE-PHE approach has a lower latency than the GA-AOMDV and LEACH-GA methods currently in use. Link faults during data transmission can be prevented by taking the communication cost and trust value into account in the adaption function. Therefore, the only time there is a minor delay is during data transfer.

Figure 3. Network Lifetime Results

The network lifespan for a specific packet size is shown in figure 3. The number of nodes is considered on the x-axis, while the network lifespan metric is considered on the y-axis. The suggested GA-DE-PHE technique is heavily used by the sensor node’s lifespan when transferring data packets. This is so that CH may apply an encryption technique to secure the data transfer. Additionally, it can be observed that the suggested approach lengthens the network lifespan as packet sizes grow. This illustrates that the suggested approach offers a longer network lifespan than previous GA-AOMDV and LEACH-GA algorithms.

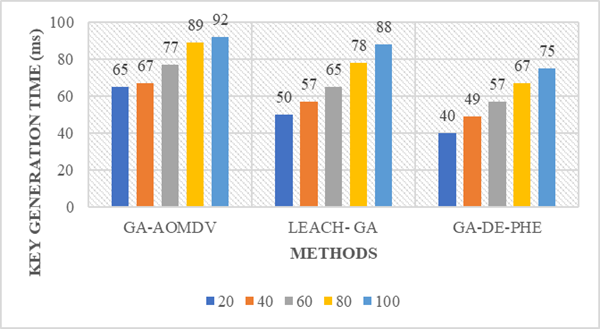
Figure 4. Key Generation Time Results

Performance evaluation based on key generation time is shown in figure 4. Performance is attained for various node counts, including 20, 40, 60, 80, and 100. We can see from the graphical representation that the suggested solution takes less time to produce keys for specific cloud customers. This is so that keys may be generated quickly and effectively using the suggested GA-DE-PHE approach. For nodes 20, 40, 60, 80, and 100, the key generation time of our suggested technique is expected to be 40 ms, 49 ms, 57 ms, 67 ms, and 75 ms, respectively.

Figure 5. Encryption Time Results

Storage security study based on encryption time for our suggested technique and alternative encryption methods as GA-AOMDV, LEACH-GA, and GA-DE-PHE is shown in figure 5. The encoding time of our suggested approach is the quickest of the five aforementioned possibilities. As a result, the suggested approach lessens the computational complexity that frequently arises during secure data transfer.

Figure 6. Decryption Time Results

The suggested works’ and other cutting-edge works’ decryption time-based storage security analysis is described in figure 6. According to the figure, our suggested approach has a quick decoding time. On the basis of the system’s capacity to fend off attacks, the security of the suggested technique is evaluated.

Figure 7. Security Level Results

In figure 7, it is observed that the security of the proposed method is superior to all other methods, such as GA-AOMDV, LEACH-GA, and GA-DE-PHE. The security level of the proposed method is 96 %, GA-AOMDV reaches 89 % and LEACH-GA reaches 94 %.

CONCLUSIONS

In this study, we will explore the utility of DE and GA in improving the energy efficiency of WSNs. Both methods aim to lengthen the network lifetime by optimising CH selection. The two algorithms are computed using the identical genetic operators, and their network lifespan, packet delivery rate, and end-to-end latency are then contrasted. Paillier’s broad homomorphic encryption algorithm was made quicker and more safe by substituting a variable called k for the precomputed hp and hq functions. This lessens the modular multiplicative inversion required for the Paillier scheme’s decoding process and demonstrates the decoding algorithm’s accuracy in terms of mathematics. According to the simulation findings, GA outperforms DE by optimising CH selection with more rounds for FND, fewer gearbox faults, and better fit. In addition to limiting and levelling out the processing power for organisations, PHE has decreased the computational effort and expense of decoding speed. In terms of rounding FND data, lowering gearbox mistakes, and enhancing CH selection ability, simulation results show that GA performs better than DE. PHE has decreased the computational effort and expenses related to decoding speed even within organisations with restricted processing capabilities.

BIBLIOGRAPHIC REFERENCES

1. Srivastava S, Singh M, Gupta S. Wireless Sensor Network: A Survey. Proceedings of International Conference on Automation and Computational Engineering. Pp. 159-63. https://doi.org/10.1109/ICACE.2018.8687059

2. Mohanasundaram R, Periasamy PS. Clustering-Based Optimal Data Storage Strategy using Hybrid Swarm Intelligence in WSN. Wireless Pers Commun. 85(3), pp. 1381-97. https://doi.org/10.1007/s11277-015-2846-8

3. Narayan V, Daniel AK. A novel approach for cluster head selection using trust function in WSN. Scalable Comput Pract Exp, 22(1), pp. 1-13. https://doi.org/10.12694/scpe.v22i1.1808

4. Al Badawi A, Polyakov Y, Aung KMM, Veeravalli B, Rohloff K. Implementation and performance evaluation of RNS variants of the BFV homomorphic encryption scheme. IEEE Trans Emerg Top Comput. 9(2), pp. 941-56. https://doi.org/10.1109/TETC.2019.2929560.

5. Kim J, Kim S, Seo J. A new scale-invariant homomorphic encryption scheme. Inform Sci. 422, pp. 177-87. https://doi.org/10.1016/j.ins.2017.08.039.

6. Garg A, Batra N, Taneja I, Bhatnagar A, Yadav A, Kumar S. Cluster Formation-Based Comparison of Genetic Algorithm and Particle Swarm Optimization Algorithm in Wireless Sensor Network. Int J Sci Res Comput Sci Eng, 5(2), pp. 14-20.

7. Amuthan A, Arulmurugan A. Analytic Network Process-Based Cluster Head Selection Mechanism for Extending the Network Lifetime, 7(12), pp. 27-34. https://doi.org/10.26438/ijcse/v7i12.2734

8. Dattatraya KN, Rao KR. Hybrid based cluster head selection for maximizing network lifetime and energy efficiency in WSN. J King Saud Univ Comput Inf Sci. 34(3), pp. 716-26. https://doi.org/10.1016/j.jksuci.2020.05.003.

9. Gong C, Chen H, He W, Zhang Z. Improved multi-objective clustering algorithm using particle swarm optimization. PLoS One. pp. 12(12). https://doi.org/10.1371/journal.pone.0188815.

10. Agrawal D, Pandey S. Optimization of the selection of cluster‐head using fuzzy logic and harmony search in wireless sensor networks. Int J Commun Syst. pp. 34(13). https://doi.org/10.1002/dac.4391.

11. Wu W, Xiong N, Wu C. Improved Clustering Algorithm based on Energy Consumption in Wireless Sensor Networks. IET Networks. 6(3), pp. 47-53. https://doi.org/10.1049/iet-net.2016.0076.

12. Wu L, Nie L, Liu B, Cui J, Xiong N. An Energy-Balanced Cluster Head Selection Method for Clustering Routing in WSN. J Internet Technol. 19(1), pp. 115-25. https://doi.org/10.3966/160792642018011901011.

13. Mumtaz J, Guan Z, Jahanzaib M, Rauf M, Sarfraz S, Shehab E. Makespan Minimization for Flow Shop Scheduling Problems using Modified Operators in Genetic Algorithm. Proceedings of 16th International Conference on Manufacturing Research, incorporating the 33rd National Conference on Manufacturing Research, pp. 435-40. https://doi.org/10.3233/978-1-61499-902-7-435

14. Silva S, Costa M, Filho CC. Customized Genetic Algorithm for Facility Allocation using P-Median. Proceedings of Federated Conference on Computer Science and Information Systems. pp. 165-9. https://doi.org/10.15439/2019F256.

15. Helsel C. Musical Cryptography Using Long Short-Term Memory Networks. 2020:1-31.

16. Kristiadi D, Hartanto R. Genetic Algorithm for Lecturing Schedule Optimization. Indones J Comput Cybern Syst, 13(1), pp. 83-94. https://doi.org/10.22146/ijccs.46357.

17. Cui L, Li G, Zhu Z, Ming Z, Wen Z, Lu N. Differential Evolution Algorithm with Dichotomy-Based Parameter Space Compression. Soft Comput, 23(11), pp. 3643-60. https://doi.org/10.1007/s00500-018-3524-8.

18. Sun G, Yang B, Yang Z, Xu G. An Adaptive Differential Evolution with Combined Strategy for Global Numerical Optimization. Soft Comput. 24(9), pp. 6277-96. https://doi.org/10.1007/s00500-019-04307-2.

19. Zaheer H, Pant M, Kumar S, Monakhov O, Monakhova E, Deep K. A New Guiding Force Strategy for Differential Evolution. Int J Syst Assur Eng Manag. 8(4), pp. 2170-83. https://doi.org/10.1007/s13198-017-0590-1.

20. Choi TJ, Togelius J, Cheong YG. Advanced Cauchy Mutation for Differential Evolution in Numerical Optimization. IEEE Access. 8, pp. 8720-34. https://doi.org/10.1109/ACCESS.2020.2963488.

21. Ogunseyi TB, Bo T. Fast decryption algorithm for paillier homomorphic cryptosystem. In: 2020 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), pp. 803-6. https://doi.org/10.1109/ICPICS50287.2020.9202361.

22. Karthick PT, Palanisamy C. Optimized cluster head selection using krill herd algorithm for wireless sensor network. Automatika, 60(3), pp. 340-8. https://doi.org/10.1080/00051144.2019.1601914.

23. Paulraj D, R LR, Jayasudha T, Ishwarya Niranjana M, Daniya T, Daniel Shadrach F. Blockchain-based Wireless Sensor Network Security Through Authentication and Cluster Head Selection. In: 2023 IEEE International Conference on Integrated Circuits and Communication Systems (ICICACS), pp. 1-5. https://doi.org/10.1109/ICICACS57338.2023.10099593.

24. Vidhya N, Seethalakshmi V, Monisha R, Dhanasekar J, Gurunathan V, Rajanandhini C. Coherent Data Transmission Using Multiplexing for a DWDM Communication System. In: 2022 IEEE 2nd Mysore Sub Section International Conference (MysuruCon), pp. 1-4. https://doi.org/10.1109/MysuruCon55714.2022.9972482.

FINANCING

The authors did not receive financing for the development of this research.

CONFLICT OF INTEREST

The authors declare that there is no conflict of interest.

AUTHORSHIP CONTRIBUTION

Conceptualization: Yuvaraja M.

Data curation: Dhanasekar J.

Formal analysis: Uma Maheswari S.

Research: Priya R. 

Methodology: Uma Maheswari S. 

Drafting - original draft: Yuvaraja M.

Writing - proofreading and editing: Dhanasekar J.