doi: 10.56294/dm2024.376
ORIGINAL
Tracking System for Living Beings and Objects: Mathematical and Graph Theory Contributions
Sistema de seguimiento de seres vivos y objetos: Aportaciones matemáticas y de la teoría de grafos
Anass Ariss1 ![]() *, Imane Ennejjai1
*, Imane Ennejjai1 ![]() *, Jamal Mabrouki1
*, Jamal Mabrouki1 ![]() *, Asmaa Lamjid1
*, Asmaa Lamjid1 ![]() *, Nassim Kharmoum1
*, Nassim Kharmoum1 ![]() *, Soumia Ziti1
*, Soumia Ziti1 ![]() *
*
1Department of Computer Science, Faculty of Sciences, Mohammed V University in Rabat. Rabat 10000, Morocco.
2Laboratory of Spectroscopy, Molecular Modelling, Materials, Nanomaterial, Water and Environment, CERNE2D, Mohammed V, University in Rabat, Faculty of Science. Rabat, Morocco.
Cite as: Ariss A, Ennejjai I, Mabrouki J, Lamjid A, Kharmoum N, Ziti S. Tracking System for Living Beings and Objects: Integration of Accessible Mathematical Contributions and Graph Theory in Tracking System Design. Data and Metadata. 2024 ;3:.376. https://doi.org/10.56294/dm2024.376
Submitted: 18-02-2024 Revised: 03-05-2024 Accepted: 19-08-2024 Published: 20-08-2024
Editor: Adrián
Alejandro Vitón Castillo ![]()
ABSTRACT
This paper presents a theoretical framework for a tracking system, wherein we generalize the formulation of a tracking system designed for living beings and objects. Many tracking systems are typically developed within specific frameworks, either for tracking in limited or unlimited space. The latter often relies on technical tools dedicated to tracking living beings or objects. In this study, we propose a system theory that formulates the task of tracking both living beings and objects. Graphical modeling is widely employed in tracking to establish correct connections between the elements to be tracked and other components in the system. However, basing a tracking system on graphs in both its theoretical and practical aspects remains the optimal method for achieving a high-performing, relevant, and adaptable system in various situations. This paper introduces a tracking system based on graph learning and hypergraphs, fully leveraging direct and indirect relations while considering the order between multiple system links. Tracking is thus formulated as a search problem on graphs and hypergraphs, with vertices representing the elements of the system (living beings or objects), and edges representing the types of connections between these elements. We define a law governing the relationships between the vertices, managing the shared data between the elements of the system and other processes. Furthermore, examples of single and multi-context tracking situations demonstrate that the proposed system, in its theoretical foundation, outperforms existing systems.
Keywords: Tracking; Tracking System; Graph; Graph Learning; Hypergraph.
RESUMEN
Este artículo presenta un marco teórico para un sistema de seguimiento, en el que generalizamos la formulación de un sistema de seguimiento diseñado para seres vivos y objetos. Muchos sistemas de seguimiento suelen desarrollarse dentro de marcos específicos, ya sea para el seguimiento en un espacio limitado o ilimitado. Este último suele basarse en herramientas técnicas dedicadas al seguimiento de seres vivos u objetos. En este estudio, proponemos una teoría de sistemas que formula la tarea de rastrear tanto seres vivos como objetos. El modelado gráfico se emplea ampliamente en el rastreo para establecer conexiones correctas entre los elementos a rastrear y otros componentes del sistema. Sin embargo, basar un sistema de seguimiento en grafos, tanto en sus aspectos teóricos como prácticos, sigue siendo el método óptimo para lograr un sistema de alto rendimiento, relevante y adaptable en diversas situaciones. En este artículo se presenta un sistema de seguimiento basado en el aprendizaje de grafos y en hipergrafos, que aprovecha al máximo las relaciones directas e indirectas y tiene en cuenta el orden entre los múltiples enlaces del sistema. Así, el seguimiento se formula como un problema de búsqueda en grafos e hipergrafos, con vértices que representan los elementos del sistema (seres vivos u objetos) y aristas que representan los tipos de conexiones entre estos elementos. Definimos una ley que rige las relaciones entre los vértices, gestionando los datos compartidos entre los elementos del sistema y otros procesos. Además, ejemplos de situaciones de seguimiento en uno o varios contextos demuestran que el sistema propuesto, en su fundamento teórico, supera a los sistemas existentes.
Palabras clave: Seguimiento; Sistema de seguimiento; Grafo; Aprendizaje de Grafos; Hipergrafo.
INTRODUCTION
The development of an effective tracking system(1) has become a paramount area of interest for researchers, particularly in light of recent phenomena such as the COVID-19 epidemic. Designing a system capable of tracking diverse entities, including living beings, poses a significant challenge, necessitating the prediction of trajectories,(3) behaviors,(4) and other intricate factors. The learning problem associated with tracking systems(1) can be conceptualized as the emergence of a multipartite graph, wherein nodes and multipartite edges (hypergraph) interconnect,(5) forming a complex web of relationships. The ultimate objective is to develop a model capable of comprehensively capturing the information embedded within this graph.
A tracking system serves as a crucial tool for monitoring trending phenomena such as epidemics. This monitoring requires precision, efficiency, and scalability. Our aim in this research is to conceptualize a universal and adaptable system capable of addressing a wide range of topics, seamlessly descending into granularities to handle diverse scenarios.
The primary objective is to simulate a tracking system with the capability to detect potential threats. This system should ensure traceability of both objects and living beings, constituting a comprehensive traceability system. The system must be versatile enough to track various prototypes, including but not limited to COVID-19, kidnapping, terrorism, etc. The predetermined prototypes and their individual metrics are integral considerations in the design of this system.
The system’s implementation will be confined to a predefined geographical space that can extend indefinitely.(6) Its model will take the form of a hypergraph,(5) enabling communication between nodes to encompass multiple contexts. The activation of these contexts will be governed by a function with multiple variables, each generated by mathematical principles, thereby constituting an optimization problem. This function defines relationships between nodes, and multiple nodes may share the same function.
In a pioneering effort, this work establishes the foundational principle of our system. It is designed to perform intricate modeling between different types of tracked elements, enhancing the learning of their characteristics to comprehend both their current state and future behavior.
Preliminaries
Elucidation and definitions
Tracking Concept
Tracking(1) is the action of monitoring the state of objects, such as living beings, and determining the position or movement of an object or living being at a specific moment or over time. This can be achieved through various methods, ranging from the application of simple theories to the utilization of cutting-edge technologies. Tracking finds applications in diverse fields, including logistics, geolocation, surveillance, counter-terrorism, and epidemiology. The remainder of this paragraph offers an overview of tracking, its historical context, fundamental concepts, and applications.
The history of tracking(1) dates back to antiquity when humans relied on footprints, animal tracks, and other signs to trail their prey and adversaries. Over the subsequent centuries, tracking techniques evolved for various purposes, including navigation, monitoring of wildlife, and criminal investigations. The foundational concepts of tracking involve identifying the object or living being to be tracked, measuring its movement, and calculating its location. Various techniques are employed to accomplish these tasks, including:
· Tracking by signs: this method involves identifying and interpreting signs left by the object or person being tracked, such as footprints, tire tracks, or DNA evidence. Trackers of signs leverage their knowledge of the environment and the behavior of the object or being to locate and interpret these signs.
· Electronic tracking: the use of electronic devices such as GPS, RFID, and Bluetooth beacons to locate and monitor the movement of objects, vehicles, and people is known as electronic tracking. These devices emit signals that can be detected and used to calculate the location of the tracked object or person.
· Visual tracking: visual tracking involves using cameras and other visual sensors to monitor the movement of objects and people. Visual trackers employ computer vision techniques to analyze images and track objects or people in real-time.
· Tracking has myriad applications across various fields. Here are a few examples:
· Wildlife tracking: tracking is employed to observe the movement and behavior of animals in their natural habitats. This information is crucial for studying their ecology, migration patterns, and social behavior.
· Criminal investigations: law enforcement uses tracking techniques to locate and monitor suspects, fugitives, and missing persons. It is also instrumental in gathering evidence in criminal cases, such as tracing a suspect’s movements before and after committing a crime.
· Transportation: tracking systems are used to monitor the movement of vehicles like trucks, ships, and airplanes. This information is utilized for enhancing route optimization, logistics management, and security.
Tracking System
A tracking system is employed to monitor an object’s position, speed, behavior, or even the health of a living being. This versatile system finds applications in various domains, including epidemics, terrorism, kidnapping, and more. Often rooted in theoretical frameworks such as graph theory, these systems are later implemented with advanced technical equipment. The remainder of this paragraph will provide an overview of tracking systems, delving into their history, underlying principles, and diverse applications.
During the Second World War, the military pioneered the use of tracking systems to monitor and locate enemy aircraft. These early systems utilized radar technology to detect the presence and movement of aircraft. Subsequent decades witnessed the evolution of tracking systems for a multitude of purposes, ranging from navigation and wildlife tracking to logistics. A tracking system comprises three essential components: a transmitter, a receiver, and a processing unit. The transmitter, affixed to the target or the person being tracked, emits a signal that the receiver captures. Analyzing the signal’s strength and direction, the receiver then transmits this information to the processing unit, which determines the location of the subject or person being tracked.
Various technologies can be employed by tracking systems to transmit and receive signals. Here are a few examples:
· The Global Positioning System (GPS): GPS, a network of satellites, is utilized by the GPS satellite tracking system to transmit signals to ground-based GPS receivers. These receivers determine their location based on signals received from at least four satellites.
· Radio frequency identification (RFID): RFID, a tracking system utilizing radio waves, identifies and tracks individuals or objects. RFID tags attached to items or people emit signals picked up by RFID readers.
· Bluetooth Low Energy (BLE): BLE, a wireless communication technology, is employed in tracking systems for indoor positioning. BLE beacons installed in a structure emit signals that smartphones or devices with BLE receivers can use to determine their location.
· Numerous applications for tracking systems span various industries. Here are a few examples:
· Transportation: the transportation industry utilizes tracking systems to monitor the location and movement of vehicles, including trucks, ships, and airplanes. This information is crucial for logistics management, enhancing security, and optimizing travel routes.
· Logistics: tracking systems in logistics facilitate the monitoring of goods flow across supply chains. These data are employed to manage shipments, track inventories, and enhance overall efficiency.
· Security: tracking systems play a vital role in maintaining law and order and security applications, locating and monitoring suspects, runaways, and missing persons. They are also utilized for asset tracking to prevent theft and loss of valuable items.
Graph Theory
This section provides an overview of graph theory,(7,8,9,10,11) encompassing its background, fundamental principles, and practical applications.
The roots of graph theory can be traced back to the 18th century when mathematicians like Euler and Hamilton delved into solving problems related to the Königsberg bridges. This problem questioned the possibility of traversing all the bridges without crossing any twice. Euler introduced the concept of a graph, using it to represent the bridges and the land masses they connected, ultimately solving the problem.
A graph,(7,8,9,10,11,12,5) denoted as G, is a pair of numbers (V,E), where V is a set of vertices and E is a set of edges. Edges connect pairs of vertices, and in graph theory, they are commonly referred to as arcs or links. Graphs can be classified based on various criteria, such as being directed or undirected, weighted or unweighted, simple or multigraph. Directed graphs, or digraphs, feature edges with a specific direction, connecting ordered pairs of vertices (u,v), where u is the source vertex, and v is the destination vertex. Weighted graphs assign a cost or weight to edges, representing various quantities like distance, time, or capacity. Simple graphs lack self-loops and multiple edges connecting the same pair of vertices, while multigraphs allow both.
Graph theory serves as a powerful mathematical tool applicable to abstractly represent and analyze real-world scenarios.(9,12) It is employed across diverse fields to solve complex problems effectively and identify optimal solutions. Viewing it as a branch of information technology mathematics, graph theory studies data structures composed of nodes connected by edges. Graphs abstractly represent elements of a scenario as nodes (also called vertices or summits) and the relationships between these nodes as edges (also called arcs), offering a way to represent real-life situations abstractly. The theory enables the analysis of these data structures and employs specialized algorithms to solve problems. Several fields leverage graph theory for various applications:
· Information Technology: trees, graphs, and linked lists are examples of data structures represented by graphs. Algorithms for shortest paths, network traffic, and correspondence issues are frequently implemented using graphs.
· The social sciences: graphs are utilized in network analysis to examine the structure and dynamics of social networks, simulating interactions between individuals, groups, and organizations.
· Operational Research: graphs are employed in optimization problems, such as the traveling salesman problem, where the goal is to find the shortest route between a set of cities and the starting point.
In our work, we extend our reliance to the generalization of graphs known as ’hypergraphs’,(5) allowing connections between more than two vertices. Hypergraphs find widespread use in computing, physical sciences, and social sciences. The conclusion of this paragraph provides an overview of hypergraphs,(12) their characteristics, and applications.
A pair (V,E) of hypergraphs H is called a hypergraph. V is a set of vertices, and E is a collection of non-empty subsets of V. Unlike a graph where an edge connects two vertices, a hyperedge in a hypergraph can connect any number of vertices. Formally, a hyperedge e can be defined as a subset of vertices with the formula E=v1,v2,...,vn. In this instance, e is termed a hyperedge of size n. A hypergraph is labeled ’uniform’ if each of its hyperedges is of the same size, otherwise, it is termed ’non-uniform.’ Several characteristics distinguish hypergraphs from graphs.
One of the most significant distinctions is the concept of the degree of a vertex. In a graph, the degree of a vertex is determined by the number of edges incident to it. In a hypergraph, the degree of a vertex is the number of hyperedges associated with it. Another crucial characteristic is the hyperdegree of a hyperedge, determined by the number of vertices it contains. In a uniform hypergraph, all hyperedges have the same hyperdegree, while in a non-uniform hypergraph, different hyperedges may have different hyperdegrees. The subsequent sentences in this paragraph will elaborate on prevalent operations that can be performed on hypergraphs.
• Union: Being given two hypergraphs H1=(V1, E1) and H2=(V2, E2) , Their union is a hypergraphe H=(V,E), where V=V1∪V2 and E=E1∪E2.
• Intersection: Given two hypergraphs H1=(V1,E1) and H2=(V2,E2), their intersection is a hypergraph H=(V,E), where V=V1∩V2 and E=E1∩E2.
• Product: Given two hypergraphs H1=(V1, E1) and H2=(V2,E2), their product is a hypergraph H=(V,E), where V=V1×V2 (the Cartesian product of V1 and V2), and E={(e1,e2)|e1∈E1 ande2∈E2}.
Hypergraphs find applications across various fields, exemplified by:
· Computer Science: hypergraphs are instrumental in data clustering algorithms, where each hyperedge represents a cluster of data points.
· Physique: hypergraphs are utilized in the study of complex systems, with each hyperedge representing a group of interacting particles.
· Social Sciences: hypergraphs are applied in network analysis, where each hyperedge represents a group of individuals with similar characteristics or behaviors.
Usefulness of Graph Theory in Tracking Systems
It is crucial to integrate graph theory(10,11) into tracking systems. Graphs serve as effective representations for the diverse components of a tracking system,(1) including sensors, tracking objects, and their interconnections. They provide a visual depiction of how different elements within a system interact and are interconnected. Adopting this approach facilitates the development of robust tracking algorithms and enables the identification of potential enhancements by modifying the graph structure.
Graph theory(9) proves invaluable in representing and analyzing the movements of objects or individuals over time. For instance, it allows the modeling of an individual’s movements after testing positive for COVID-19 or monitoring child abductions. Elements to be tracked are defined as nodes on the graph, and the contextual connections between these elements are represented as edges. Graph algorithms can then be applied to find the shortest path between nodes or determine the most frequented points of passage for a tracked element.
Furthermore, graphs are adept at illustrating the relationships between different elements within a tracking system, be it the various fields of application used for tracking an object or person or the diverse data collected by the system.(7,1) By leveraging graphs, a comprehensive understanding of the relationships and interactions between elements is attainable, offering valuable insights for optimizing the operation of the tracking system.(14)
Categories of Tracking Systems
The various types of tracking systems share a common objective: to assess the effectiveness, precision, and reliability inherent to each system type. Results naturally vary based on specific applications, environmental conditions, and precision requirements. Tracking systems, like any technology, come with both advantages and disadvantages. The ultimate aim is to pinpoint the most suitable system to meet particular needs. Factors for comparison encompass precision and dependability, ease of use, costs, and adaptability. These systems can be categorized based on their data collection and analysis capabilities into four distinct types:
· Localization Tracking Systems: these systems track and map the position and movement of physical entities.(88)
· Tracking Systems for Activities: this category involves tracking and recording the activities of physical or virtual entities.(80)
· Performance Tracking Systems: such systems monitor and measure the performance of physical or virtual entities.(81)
· Data Tracking Systems: this category encompasses systems designed to track and analyze data generated by physical or virtual entities.(18)
In conclusion, the Preliminaries section lays the groundwork for a systematic and reliable exploration of evaluating the reliability of graph theory in tracking systems, it’s crucial to underscore that the quality of results is intricately tied to the quality of the data employed. When the data used to model a tracking system are both precise and comprehensive, graph theory proves highly valuable in comprehending system dynamics and addressing challenges. Conversely, if the data utilized are incomplete or inaccurate, the results derived may lack reliability.
Related work
Tracking based on graphs. A graph is made up of peaks (which can be pixels, superpixels, or object parts) and valleys (hyperhedron correspondence between the nodes). The graphs are used to predict the labels of non-tagged summits. Algorithms based on graphs have been used successfully for object detection,(19) recognition of human activities,(20) and recognition of faces.(21) In general, trackers based on graphs use superpixels as nodes to represent the appearance of the object, whereas edges represent the internal geometric structure. Another strategy is to create graphs between the parts of the objects in different images. Many trackers have been created using graphs.(22,6,23,24,25)
Tracking has been successfully extended to multi-target scenarios in recent years.(26,27,28) The Multi-target tracking is not primarily focused on an appearance model. Appearances are an important indicator, but in MTT (Multi-Target Tracking) scenarios, relying solely on appearances can cause issues if the scene is highly cluttered or if the targets have the same appearance. Towards that end, some studies have focused on improving appearance models,(29) while others have combined target and target-not appearances.(30,31,32,33,34,35,3) Simple models are frequently used in MTT. For greater simplicity, many models are based on raw bitmap representations,(33,36,37,32,38) whereas color histograms are the most commonly used representation for modeling appearance in MTT approaches.(34,39,40) Other approaches make use of covariance matrix representations, pixel comparison representations, SIFT characteristics, or pose characteristics.(41,42,43,44,45) Recently, deep neural network architectures have been used to model perception.(46,47,48) In these architectures, high-level features are extracted by convolutional neural networks entrapped for specific tasks.
A target’s movement model describes how the target moves. The movement index is an important indicator for MTT. Indeed, knowing the likely location of the target in future images reduces search space and improves the accuracy of the appearance model. The most commonly used migration models in the MTT are classified as linear and nonlinear migration models. A linear movement motif follows a linear movement at a constant speed from one image to the other. This simple movement model is one of the most popular in MTT.(29, 90, 91, 92, 93) However, linear movement models are frequently incapable of dealing with occlusion over time. To improve this, nonlinear movement models with more precise predictions have been proposed.(49,50,51)
The majority of tracking techniques assume that each target has independent movement patterns. This simplification may be problematic in the bound scenes. Interaction models capture the interactions and forces between different targets in a scene.(52,53,54) The most common interaction models are the social force model introduced by Helbing et al.(52) and the mass movement model.(53) The social power model is also known as the group power model. In these models, each target responds to a potential energy source caused by force interactions (repulsive or attractive) with other objects while attempting to maintain a desired speed and direction of movement.(30,31,32,33,34,35,3) The models of mass movement are another type of interaction model used in the MTT and are inspired by the literature on mass simulation.(55,56) This type of model is typically used for entangled scenes.(57,58,59,60,61,62) The main disadvantage of most of these methods is that they are limited to a few terms of force designed for the hand, such as collision avoidance and group attraction. Recently, Arahi et al.(31) proposed using long short-term memory networks for reasoning with multiple people (dubbed LSTM social). They presented a framework for forecasting the long-term trajectory of all targets.
To our knowledge, there hasn’t been a comprehensive review of the literature on the topic of the following several objects. However, there are other reviews related to the tracking of many objects; we categorize these studies into four groups and discuss the differences with the others as follows.
· The first series(65,4,66,64,63) deals with tracking as an individual component, whereas this work specifically deals with various elements of tracking several objects. For instance, object tracking is treated as a step in the process of high-level tasks such as foul model simulation.(65,4,66) The following of objects is also examined in a study(64,63) as a component of a system for behavior recognition(64) or video surveillance.(63)
· The second series(67,69) is devoted to general visual tracking approaches(67,68) or to specific problems such as models of appearance in visual tracking.(69) In contrast, their inquiry area is more extensive than ours and is focused on the tracking of numerous objects.
· The third series(70,71) presents and discusses benchmarks for visual object tracking in general(70) and multi-object tracking in particular.(71) Instead of reading literary reviews, their focus is on experimental studies.
· The fourth series(72) reviews recent advancements and developments in object detection made possible by deep learning. The subject is related to the last yet different. While the MOT must combine these data over multiple photos to generate the object’s trajectories, object detection can provide observations for tracking based on detection by localizing the potential locations of the object in each image. To determine the object’s trajectories, multiple photos are needed.
Several systems of tracking multiple objects use tracking-by-detection as a general framework.(18,73,74) In this context, objects are first identified and then linked to various photographs. Due to concurrent developments in multiple object detectors,(75,76,77,78) the strategies that follow this line of approach focus more on the element of data association for the following. These methods can be divided into two main categories: local and global monitoring methods. The local methods(79,80,81) only consider two photos when associating data. This makes them calculatingly effective, but their performances are sensitive to factors that are irrelevant to tracking, such as camera movement, stance variation, etc. Contrary to local methods, global strategies(82,83,84) accomplish data association by using a larger number of images. Recent approaches in this direction turn data association into a network flow problem.(85,86,87,88)
Problem formulation
· The
type of connection or the establishment of an inter-node link is defined based
on the value of the ![]() law,
as illustrated in figure 1. This figure represents the modeling of a
multi-context tracking system, incorporating zero or multiple context-type
relationships between nodes. The modeling includes indirect relations and the
implementation of tracking laws specifying the type of direct relations among
system elements. This approach is based on the principle of hypergraphs.
law,
as illustrated in figure 1. This figure represents the modeling of a
multi-context tracking system, incorporating zero or multiple context-type
relationships between nodes. The modeling includes indirect relations and the
implementation of tracking laws specifying the type of direct relations among
system elements. This approach is based on the principle of hypergraphs.
· Each node can interact with other nodes in various contexts. In fact, a studied hypergraph may have several context graphs, as shown in figure 1, defining the modeling of a tracking system with separate contexts. Each node can have one or more clones (duplicates) for other clouds of contexts, resulting in multiple context graphs for the original hypergraph.
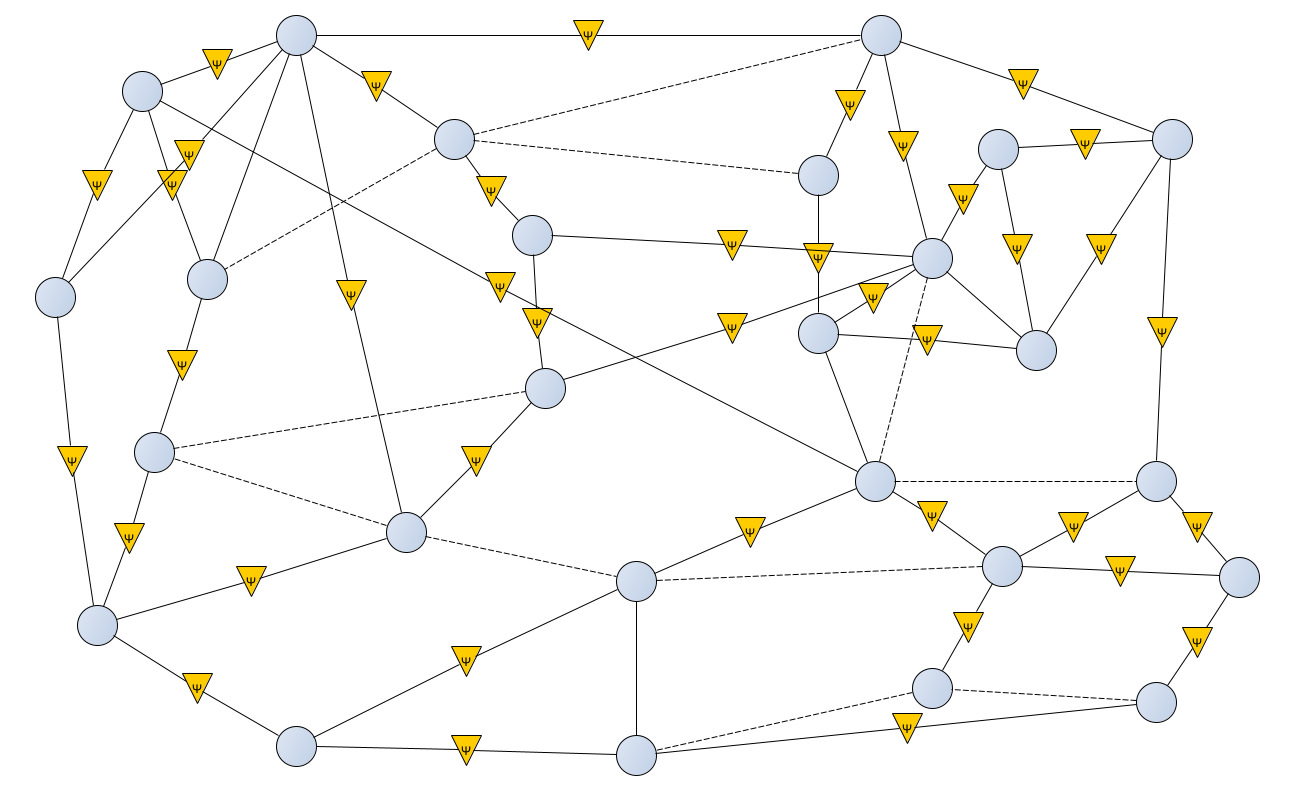
Figure 1. Modeling of a multi-context tracking system
1. Depending on the context, each node may have a dynamic clone.
2. There is always a connection between the traits of each node and its clones.
3. Since the metric used to define the type of connections differs for each pair of nodes in the system, it’s possible that one pair of nodes contains fewer contexts than others.
4. The maximum number of contexts that can exist between pairs of nodes is the size of the system’s contexts.
5. The data from each node is presented in the following order: public, neighborhood, and private.
6. In this stage, the shared data structure between nodes is not highlighted.
7. Each pair of nodes can have an infinite number of relationships.
8. The characteristics are updated when the clone of the node returns to its environment or leaves for another environment. Some fundamental questions arise at this point:
· What parameters (context, etc.) should be activated in each environment?
· What parameters (context, etc.) are shared between all environments?
· What are the management rules and the definition of these parameters?
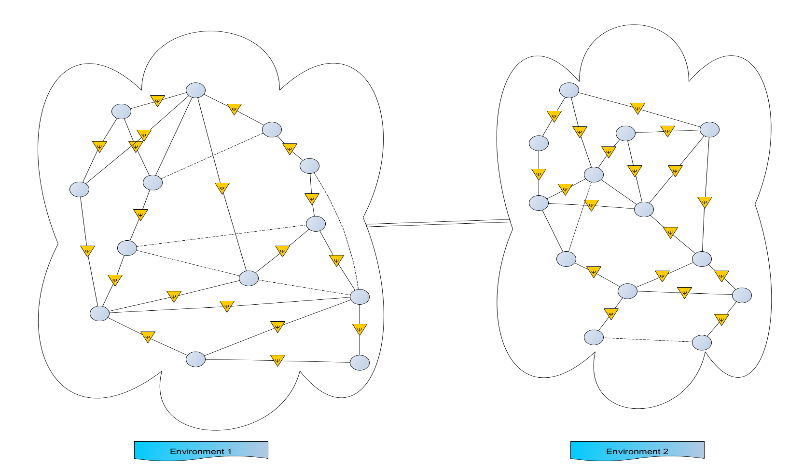
Figure 2. Modeling of a context-separated tracking system
1. Moving each node from one environment to another triggers a metric, leading to the question:
· How will it be detected that a node has changed the environment?
2. Once it’s certain that a node has changed the environment, a trigger will cause the system to update the node’s profile (i.e., a dynamic system).
3. Zones and sub-zones (contextual zones) can be created, where each zone communicates with others through common data between contexts.
4. The directions of all nodes need to be registered in a structure.
5. It’s necessary to know all the contexts of the nodes and consider both old and new contexts.
6. The method of communication between nodes is crucial (mail, IoT, etc.), as well as the types of data (structured, unstructured, ...). This information will be processed later in a data preprocessing layer.
7. Each node in a tracking system has communication characteristics.
· Example: the common point between persons X, Y, and Z is the context of scientific research, which can be communicated either by direct or indirect means, as shown in figure 2. This is a modeling of a single-context tracking subsystem, where one or more nodes can be in other subsystems.
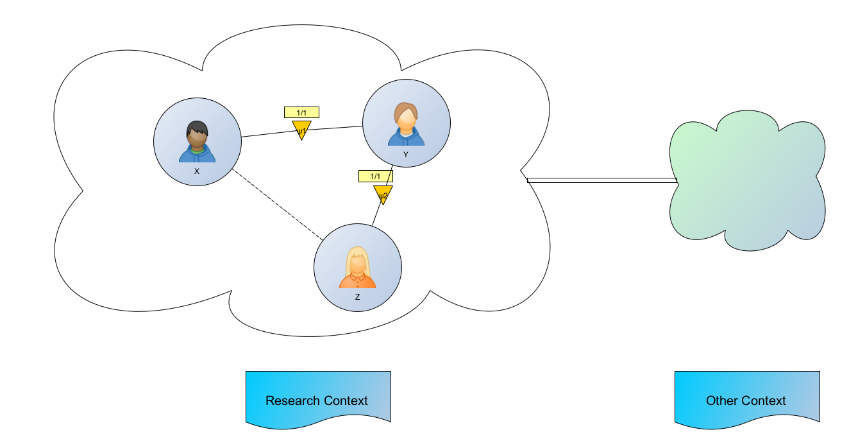
Figure 3. Modeling of a single-context tracking system
Robustness analysis and proposed system approach
Two situations need to be taken into account in a tracking system, that of an oriented system figure 4 and that of a non-oriented system figure 3. In the course of this research, we have paid particular attention to the case of an oriented tracking system.
Basic Concepts of a Tracking System
Ts=〈V,E,δ,Ψ,I-,I+〉
Where:
V: Set of vertices "nodes".
E: Set of edges "link".
δ:E⟶V×V/{{x,y}|(x,y)∈V^2∧x≠y}. Incidence function that associates to each edge, a pair of vertices.
Ψ: Delta Tracking Law (DTL). The law defines the type of direct relationship between the elements in the system.
I-:V×E↦∑(xi,xj)∈Vn)∈Vn Σ(xi,xj). xi≠xj; i≠j. Is the application of the previous nodes.
I+:V×E↦∑(xi,xj)∈Vn)∈Vn Σ(xi,xj). xi≠xj; i≠j Is the application of the following nodes.
We also use the notion:
I=I+-I- and I is called the impact matrix of the system.
Contextual System
A contextual tracking system is a couple of:
∑=〈Ts,Ctx〉
Where:
Ts is the tracking system.
Ctx is the initial context, it is an application.
Ctx:V↦δ
Ctx(V) is the number of contexts contained in the node V, these are the different contexts that a node can have.
Associated tracking system and matrix concepts
We can associate a tracking system with a hypergraph which has nodes that can have several shapes according to the contexts they belong to. One or more arcs link a node to a DTL if and only if I-(v,ψ)≠0. One or more arcs connect a DTL to a node if and only if I+ (v,ψ)≠0. The non-zero values of the matrices I- and I+ are associated with the arcs as labels (by default it takes the values of context IDs).
All tracking systems are perfect
An oriented tracking system Ts is perfect if and only if:
∀v∈Vand∀ψ∈Ψ:I-(v,ψ)⋅I+(v,ψ)=0
The system does not include any elementary loop, i.e. no Ψ law having the same node in input and in output.
Signage
The signaling S, is the data neighborhood that the node can propagate with the outside. The signaling can be represented by a multi-dimensional vector, having for length the number of contexts taken by the node. The system must be treated in two directions for these edges E, we define the first direction of stops according to the first belonging to the context.
I-, I+, and I are matrices whose number of rows is equal to the number of vertices, and the number of columns is equal to the number of DTL.
We note I- (.,ψ), I+ (.,ψ) and I(.,ψ) the columns of these matrices associated to a ψ law.
There are two cases to be dealt with in a tracking system, that of an oriented system figure 4 and that of a non-oriented system figure 3. In this study, our main focus is on the case of an oriented tracking system. Let us consider for example figure 4. It defines a oriented tracking system with a maximum of three contexts, direct and indirect relations, as well as the tracking law that defines the context of relation between the elements of the system and the indication of the number of contexts activated for each pair of nodes, tha’s define as follows:
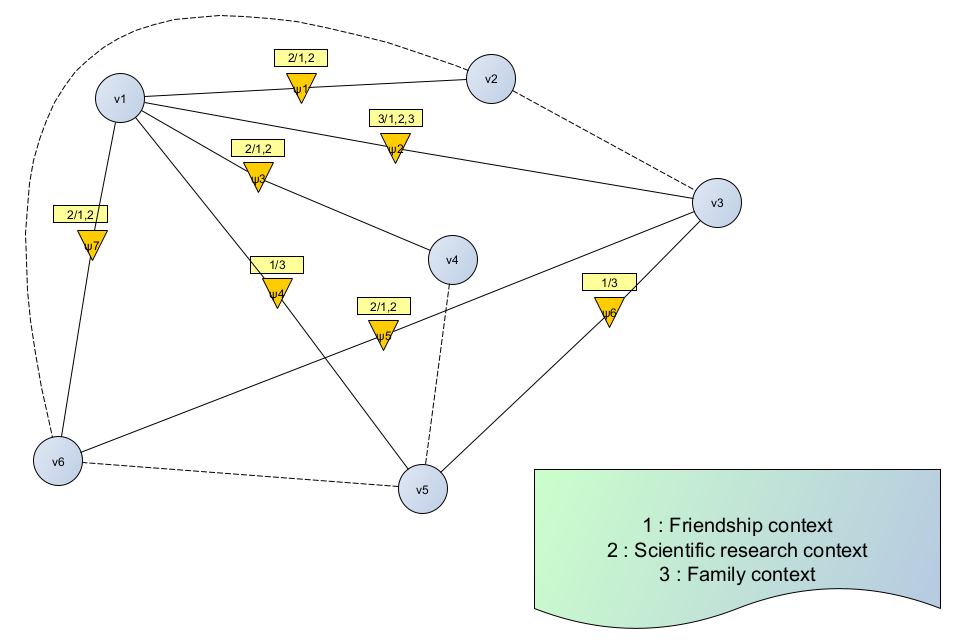
Figure 4. Modeling a non-oriented tracking system with up to three contexts

We then have:

The initial signage is:
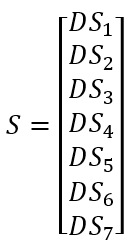
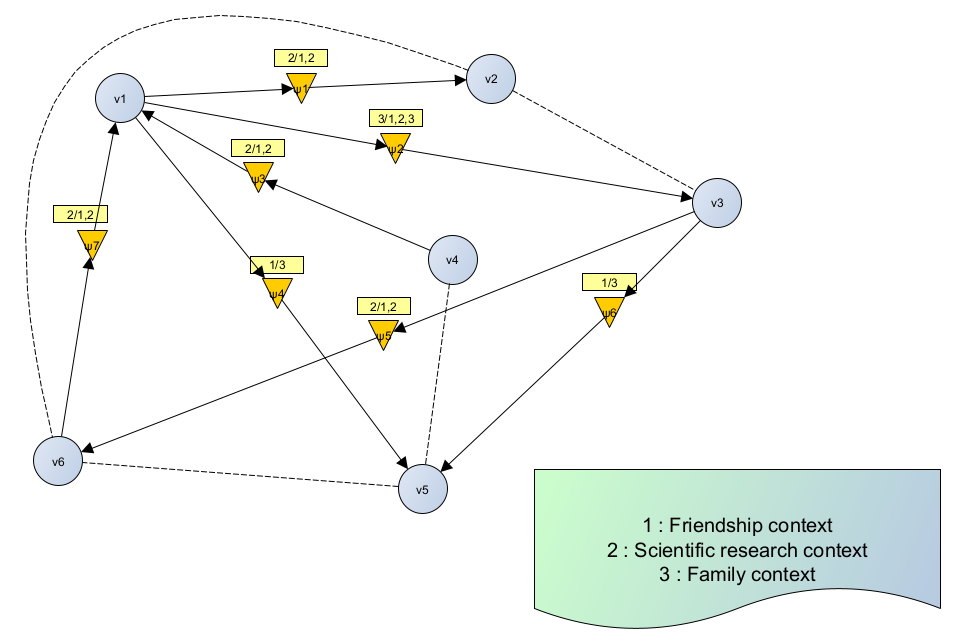
Figure 5. Modeling an oriented tracking system with up to three contexts
DSi is a data structure shared by the node according to its context. The DSi can contain different types of public, private and neighbor data from nodes in different contexts.
DTL is a traversable law
A Ψ law is said to be traversable if and only if:
∀v∈V,S(v)⩾I- (v,ψ)
We can express that ψ is traversable by the notations:
S⩾I- (.,ψ)
S→ψ
For example in figure 4, an oriented tracking system with initial signaling:
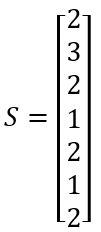
Where the elements of S represent the number of data structures DSi according to the context for each law ψi.
The laws ψ1 and ψ3 are traversable because:

Transversal of a law Ψ
If ψ is traversable for S signaling, traversing ψ gives a new S' signaling such that:
![]()
For example in the system of figure 4, we discuss the traversement of ψ1 from the initial S signaling, so we get the following S' signaling:

Conflict and parallelism
Structural conflict
Two DTLs ψi and ψj are in structural conflict if and only if they have at least one vertex in common:
![]()
Effective conflict
Two DT Ls ψi and ψj are in effective conflict for a signaling S if and only if ψi and ψj are in structural conflict such that:
![]()
Structural parallelism
Two DTLs ψi and ψj are structurally parallel if.
![]()
They have no common entry vertex (the scalar product of their I- vectors is null)
Effective parallelism
Two DTLs ψi and ψj are effective parallel for a given signaling S if and only if they are structurally parallel:
![]()
Basic concepts
In the oriented tracking system of the figure 4, the DTLs ψ1 and ψ2 are in structural conflict since :
![]()
On the other hand the ψ5 and ψ7 laws are structurally parallel. Indeed:

For initial signaling S, the laws ψ1 and ψ2 are ineffective conflict.
If we now consider the signalling.

W ⃗ the vector whose components the 0 values in S' represent respectively v1 and v6 that they have no context to take, which can be considered as a contestable element, then the laws ψ5 and ψ7 are effectively parallel (they can be traversed independently of each other).
Traversable sequence
We consider figure 4 three signals S0, S1 and S2, S0 →(ψ2) S1 and S1 →(ψ4) S2, we say that the sequence (ψ2,ψ4) is traversable from S0, which:
S0 →(ψ2,ψ4)S2
Let W ⃗ be the vector whose components W ⃗(Ψ) are the number of activation of Ψ laws (number of occurrences) in a traversal sequence S. This vector is called the characteristic vector of S. Its dimension is equal to the number of Ψ laws in the tracking system.
Still considering the tracking system of the figure 4, we have for example for the sequence S=(ψ2,ψ2,ψ3):
It is assumed that:

Where we simulate this time DSi the data structure shared with the nodes, by the quantity of the cotexts shared with the nodes.

The evolution of the signalisations of a tracking system is then given by the fundamental equation I⋅¯S.
![]()
For our example:

The possibility of creating signaling graphs is a fascinating prospect, especially in a particular context. The notion of signaling graphs can be interpreted in a variety of ways, depending on the application domain or context. A concrete example might be a signaling graph, a graphical representation in the form of a tree structure, highlighting the exchange of data between different components of a tracking system. These graphs are of crucial importance in various fields, such as telecommunications, molecular biology, financial markets, crisis management (terrorism, kidnapping, epidemics), computer science and artificial intelligence.
Each field interprets and applies these signaling graphs in its own specific way, using them as visual tools to understand information flows, interactions, or signals that influence decisions. Whether we’re talking about communication networks, biological processes, financial indicators, or mechanisms for robustly tracking phenomena that have a direct impact on society, such as terrorism, kidnapping or epidemics, these graphs are proving to be invaluable tools. In this way, our tracking system could evolve into a powerful tool for analyzing and optimizing various complex systems.
We can build signaling graphs, for example:

Here are some possible developments of this idea in different contexts:
Telecommunications Network
In the field of telecommunications, signaling graphs could refer to graphical representations of signaling flows between network nodes. This could include signaling protocols such as SIP (Session Initiation Protocol) in VoIP communications.
Molecular Biology
In molecular biology, signaling graphs could represent cellular signaling pathways, showing how signaling molecules interact within cells to regulate various biological processes.
Finance and Market Analysis
In the financial domain, signaling graphs could represent indicators or signals that influence investment decisions. For example, graphs could illustrate correlations between different financial indicators.
Computer Science and Distributed Systems
In computer science, signaling graphs could refer to the graphical representation of signal exchanges between different components of a distributed system. This could include messages, events, or other forms of communication between modules.
Machine Learning and Neural Networks
In the field of machine learning, signaling graphs could represent the propagation of signals through the layers of a neural network. This could be used to understand how information is processed and propagated through the model.
Terrorism
In the context of counterterrorism efforts, signaling graphs can be applied to analyze patterns of communication and coordination among suspected individuals or groups involved in terrorist activities. By mapping out the network of communication, security agencies can gain insights into potential threats and take preventive measures to ensure public safety.
Kidnappings
For law enforcement and security purposes, signaling graphs can be utilized to study and understand communication patterns related to kidnapping incidents. Analyzing the network of communication among perpetrators, accomplices, and potential victims can aid in tracking and preventing kidnapping cases. This approach contributes to the development of effective strategies for law enforcement agencies.
Epidemics
In the field of public health, signaling graphs play a crucial role in tracking the spread of epidemics. By modeling the interactions between individuals, monitoring travel patterns, and analyzing communication networks, health authorities can predict and respond to the spread of infectious diseases. Signaling graphs contribute valuable insights for implementing containment measures and mitigating the impact of epidemics on communities.
Depending on the specific context in which the idea is introduced, it would be important to provide additional details for a deeper understanding and to guide the development of this idea in a particular direction.
Set of accessible signage
The set of accessible signage AS(Ts,S0) of a signaled tracking system is the set of signages that can be reached from the initial signage S0 by a traversal sequence.
![]()
We can, when this set is finite, represent it as a graph GAS(Ts,S0).
This graph has for set of vertices the set of accessible signalizations AS(Ts,S0), a directed arc connects two vertices Si and Sj if there exists a traversables DTL allowing to pass from a signalizations to another one according to an activated context: Si→Ψ Sj
In general, the arcs of the graph are labeled according to the context and the corresponding ψi law.
Set of rules and tracking system
Tracking System
We have observed that a tracking system can be conceptualized from one of the following perspectives:
A graph with multiple types of edges exhibiting dynamic behavior.
A collection of matrices whose dynamic behavior is elucidated by the fundamental equation of the linear system.
The tracking system can also be viewed as a knowledge production system (deduction system), alternatively known as a rule system. It is based on knowledge representation in the form:
![]()
System of rules
A system of rules, regulations, or knowledge creation is established with the following characteristics:
It is grounded in facts, where a context of known facts is enhanced by rules that enable the deduction of new facts.
It utilizes an inference mechanism, specifically deduction.
The inference mechanism involves listing all rules (contexts) at each system iteration and iteratively traversing that list. When a rule’s prerequisites for a certain situation are met, the rule becomes applicable. The inference mechanism stops if no rule is applied or if a final fact (conclusion) is confirmed.
In a complex environment, multiple rules may be applicable, and the outcome of deduction may vary based on whether one applies one rule at a time or all simultaneously. The fundamental mechanism often selects the first encountered option without considering other possibilities, leading to a scenario known as conflict when multiple rules apply. Conflict resolution, also referred to as control, defines the inflection mechanism, which can become intricate.
In the case of a tracking system:
The foundation of the rules lies in the matrices I- and I+, exploited by column (i.e., the entire set of laws ψi with their traversal rules).
The initial context is the original initial signaling.
Conflict resolution is influenced by concepts in the parallel law Ψ (where the traversal order is random) and conflict transitions (when the outcome depends on the traversal order). In cases of ineffective conflict between two laws ψi and ψj, one law is chosen to be followed, while the other is left unfollowed.
Grammar
A tracking system, on the other hand, represents a very specific type of rule system. The knowledge base is not general, as it is constructed solely based on the concept of node signalizations, i.e., the values of a complete set of attributes.
This concept can be expressed using constructed words in an alphabet. The alphabet is a set of node identifications, such as {v1,v2,v3}, for example. Signalizations, where node v1 contains three contexts according to law ψ2 and node v3 contains three contexts according to law ψ4, can be represented as follows:
![]()
We can define an application ψ that, given any signal S, associates a word ψ(S) in v*.v*, where v* is the set of finite sequences of elements of V including the empty element ψ. The specific class of rule-based systems corresponding to tracking systems is known as a grammar (word-rewriting system).
The grammar G=〈T,Q〉 associated with the network Ts=〈V,E,δ,Ψ,I-,I+〉 is defined by:
Its terminology T.
The entire set Q of rewriting rules:
![]()
Is is the initial signalization S from the tracking system, corresponding to Is=ψ(S), from which new words can be derived, creating a tracking chain. When considering traversal sequences, if Ψ is viewed as an alphabet, Ψ* represents the entire set of traversal sequences, and for the elements of Ψ*, the order in which the elements appear is important. Signalizations, on the other hand, are elements of V* where order is irrelevant.
For example, consider the non-oriented tracking system in figure 3. If we view it as a grammar, we have:

The entire set of available signalizations can then be written as:
![]()
This aspect is significant as it allows for concise notations and, more importantly, bridges the gap between our tracking system and artificial intelligence techniques.
To sum up our findings, this section has presented a detailed initial contribution on the theory of a tracking system, this system can be viewed from various perspectives, each with its own set of advantages and disadvantages. A reasonable-sized graph produces an easily transferable description that clearly explains certain synchronization mechanisms. The number of data types for each node is characterized in signalizations, and each type exists in a flow, which will be passed later in the edges corresponding to the context.
The material aspect, as summarized
by the fundamental equation, characterizes a subset (since ![]() must
be a traversable sequence) of the signalizations accessible via a linear
equation system. This is critical during the analysis.
must
be a traversable sequence) of the signalizations accessible via a linear
equation system. This is critical during the analysis.
A tracking system can be considered as a particular rule system. This aspect is particularly interesting during production in more general context-oriented artificial intelligence techniques.
Advantages of tracking systems
A tracking system based on graph theory and hypergraph theory can offer several advantages, including:
Clear Representation of Relationships: graphs and hypergraphs provide a clear and easily understandable representation of relationships between various elements. This facilitates data visualization, trend detection, and model identification.
Effective Data Manipulation: hypergraphs excel in modeling complex data that might be challenging to represent using traditional graphs. This enables efficient processing of large datasets.
Identification of Groups and Communities: graphs and hypergraphs can identify groups and communities of elements sharing common characteristics. This is valuable for analyzing social networks, detecting fraud, and identifying clusters of similar users.
Real-time Tracking of Data Changes: graphs and hypergraphs can be updated in real-time to reflect changes in the data. Real-time tracking enables the detection of significant changes as data evolves.
Adaptability to Different Data Types: graphs and hypergraphs are versatile in representing various data types, including structured and unstructured data. This versatility supports comprehensive data analysis and a holistic representation of relationships between diverse elements.
CONCLUSIONS
This paper uses the concepts of graphs and hypergraphs to provide a theoretical tracking system for both live things and objects. In contrast to previous techniques based just on graphs, the suggested method offers broad application by modeling a multi-context linking system. Based on hypergraphs, our method extends to graphs as a particular instance and presents a tracking law for data processing and sharing. This new tracking law allows for many system interactions, resulting in a flexible and dynamic approach that may be used in a variety of situations. In order to increase the system’s flexibility, future work should concentrate on improving system performance and improving theoretical elements.
BIBLIOGRAPHIC REFERENCES
1. Hallinan, Maureen T.” Tracking: From theory to practice.” Sociol- ogy of education 67.2 (1994): 79-84.
2. S. Pellegrini, A. Ess, and L. Van Gool. Improving data association by joint modeling of pedestrian trajectories and groupings. In Eu- ropean Conference on Computer Vision, pages 452–465. Springer, 2010.
3. S. Pellegrini, A. Ess, and L. Van Gool. Improving data association by joint modeling of pedestrian trajectories and groupings. In Eu- ropean Conference on Computer Vision, pages 452–465. Springer, 2010.
4. W. Hu, T. Tan, L. Wang, S. Maybank, A survey on visual surveil- lance of object motion and behaviors, IEEE Trans. Syst. Man Cy- bern., Part C, Appl. Rev. 34 (3) (2004) 334–352.
5. Bretto, Alain.” Hypergraph theory.” An introduction. Mathemati- cal Engineering. Cham: Springer (2013).
6. Dawei Du, Honggang Qi, Longyin Wen, Qi Tian, Qingming Huang, and Siwei Lyu. 2017. Geometric hypergraph learning for visual tracking. IEEE TC 47, 12 (2017), 4182–4195.
7. Tutte, William Thomas, and William Thomas Tutte. Graph theory. Vol. 21. Cambridge university press, 2001.
8. West, Douglas Brent. Introduction to graph theory. Vol. 2. Upper Saddle River: Prentice hall, 2001.
9. Gould, Ronald. Graph theory. Courier Corporation, 2012.
10. Bollob´as, B´ela. Modern graph theory. Vol. 184. Springer Science & Business Media, 1998.
11. Bondy, John Adrian, and Uppaluri Siva Ramachandra Murty. Graph theory with applications. Vol. 290. London: Macmillan, 1976.
12. Bretto, Alain.” Hypergraph theory.” An introduction. Mathemati- cal Engineering. Cham: Springer (2013).
13. Hopkins, Brian, and Robin J. Wilson.” The truth about K¨onigsberg.” The College Mathematics Journal 35.3 (2004): 198- 207.
14. Hallinan, Maureen T.” Tracking: From theory to practice.” Sociol- ogy of education 67.2 (1994): 79-84.
15. H. B. Shitrit, J. Berclaz, F. Fleuret, and P. Fua, “Multi-commodity network flow for tracking multiple people,” IEEE TPAMI, vol. 36, no. 8, pp. 1614–1627, 2014.
16. D. Reid et al., “An algorithm for tracking multiple targets,” IEEE transactions on Automatic Control, vol. 24, no. 6, pp. 843–854, 1979.
17. G. Shu, A. Dehghan, O. Oreifej, E. Hand, and M. Shah, “Part- based multiple-person tracking with partial occlusion handling,” in Proc. CVPR. IEEE, 2012, pp. 1815–1821.
18. Y. Tian, A. Dehghan, and M. Shah, “On detection, data association and segmentation for multi-target tracking,” IEEE Transactions on Pattern Analysis and Machine Intelligence, pp. 1–1, 2018.
19. Idir Filali, Mohand Sa¨ıd Allili, and Nadjia Benblidia. 2016. Multi- scale salient object detection using graph ranking and global–local saliency refinement. Elsevier Signal Proc. Image 47 (2016), 380–401.
20. Meng Li and Howard Leung. 2016. Multiview skeletal interaction recognition using active joint interaction graph. IEEE TM 18, 11 (2016), 2293–2302.
21. H. K. Meena, K. K. Sharma, and S. D. Joshi. 2017. Improved facial expression recognition using graph sig. pro. IET EL 53, 11 (2017), 718–720.
22. Dawei Du, Honggang Qi, Wenbo Li, Longyin Wen, Qingming Huang, and Siwei Lyu. 2016. Online deformable object tracking based on structure-aware hyper-graph. TIP 25, 8 (2016), 3572–3584.
23. H. Nam, M. Baek, and B. Han. 2016. Modeling and propagating CNNs in a tree structure for visual tracking. CoRR. Retrieved from abs/1608.07242.
24. Tao Wang and Haibin Ling. 2018. Gracker: A graph-based planar object tracker. IEEE TPAMI 40, 6 (2018), 1494–1501.
25. D. Yeo, J. Son, B. Han, and J. H. Han. 2017. Superpixel-based tracking-by-segmentation using Markov chains. In Proceedings of the CVPR. IEEE, 511–520.
26. K. Okuma, A. Taleghani, N. De Freitas, J. J. Little, and D. G. Lowe. A boosted particle filter: Multitarget detection and tracking. In Computer Vision-ECCV 2004, pages 28–39. Springer, 2004.
27. C. Huang, B. Wu, and R. Nevatia. Robust object tracking by hierarchical association of detection responses. In Computer Vi- sion–ECCV 2008, pages 788–801. Springer, 2008.
28. Y. Xiang, A. Alahi, and S. Savarese. Learning to track: On- line multi-object tracking by decision making. In Proceedings of the IEEE International Conference on Computer Vision, pages 4705–4713, 2015.
29. M. D. Breitenstein, F. Reichlin, B. Leibe, E. Koller-Meier, and L. Van Gool. Robust tracking-by-detection using a detector confidence particle filter. In Computer Vision, 2009 IEEE 12th International Conference on, pages 1515–1522. IEEE, 2009.
30. Robicquet, A. Sadeghian, A. Alahi, and S. Savarese. Learning so- cial etiquette: Human trajectory understanding in crowded scenes. In European Conference on Computer Vision, pages 549–565. Springer, 2016.
31. Alahi, K. Goel, V. Ramanathan, A. Robicquet, L. Fei-Fei, and S. Savarese. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 961–971, 2016.
32. S. Pellegrini, A. Ess, K. Schindler, and L. Van Gool. You’ll never walk alone: Modeling social behavior for multi-target tracking. In Computer Vision, 2009 IEEE 12th International Conference on, pages 261–268. IEEE, 2009.
33. K. Yamaguchi, A. C. Berg, L. E. Ortiz, and T. L. Berg. Who are you with and where are you going? In Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on, pages 1345–1352. IEEE, 2011.
34. W. Choi and S. Savarese. Multiple target tracking in world co- ordinate with single, minimally calibrated camera. In Computer Vision–ECCV 2010, pages 553–567. Springer, 2010.
35. P. Scovanner and M. F. Tappen. Learning pedestrian dynamics from the real world. In Computer Vision, 2009 IEEE 12th Inter- national Conference on, pages 381–388. IEEE, 2009.
36. S. Ali and M. Shah. Floor fields for tracking in high density crowd scenes. In Computer Vision–ECCV 2008, pages 1–14. Springer, 2008.
37. Z. Wu, A. Thangali, S. Sclaroff, and M. Betke. Coupling detection and data association for multiple object tracking. In Computer Vi- sion and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 1948–1955. IEEE, 2012.
38. S. Oron, A. Bar-Hillel, and S. Avidan. Real-time trackingwith-detection for coping with viewpoint change. Machine Vision and Applications, 26(4):507–518, 2015.
39. S. Tang, B. Andres, M. Andriluka, and B. Schiele. Multiperson tracking by multicut and deep matching. In European Conference on Computer Vision, pages 100–111. Springer, 2016.
40. N. Le, A. Heili, and J.-M. Odobez. Long-term time-sensitive costs for crf-based tracking by detection. In European Conference on Computer Vision, pages 43–51. Springer, 2016.
41. H. Izadinia, V. Ramakrishna, K. M. Kitani, and D. Huber. Multi-pose multi-target tracking for activity understanding. In Applica- tions of Computer Vision (WACV), 2013 IEEE Workshop on, pages 385–390. IEEE, 2013.
42. R. Zamir, A. Dehghan, and M. Shah. Gmcp-tracker: Global multi-object tracking using generalized minimum clique graphs. In Computer Vision–ECCV 2012, pages 343– 356. Springer, 2012.
43. Y. S. Khanloo, F. Stefanus, M. Ranjbar, Z.-N. Li, N. Saunier, T. Sayed, and G. Mori. A large margin framework for single cam- era offline tracking with hybrid cues. Computer Vision and Image Understanding, 116(6):676– 689, 2012.
44. S. Hong and B. Han. Visual tracking by sampling treestructured graphical models. In European Conference on Computer Vision, pages 1–16. Springer, 2014.
45. H. Nam and B. Han. Learning multi-domain convolutional neural networks for visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4293–4302, 2016.
46. D. Held, S. Thrun, and S. Savarese. Learning to track at 100 fps with deep regression networks. In European Conference on Com- puter Vision, pages 749–765. Springer, 2016.
47. L. Leal-Taixe, C. Canton-Ferrer, and K. Schindler. Learning ´ by tracking: Siamese cnn for robust target association. arXiv preprint arXiv:1604.07866, 2016.
48. M. Zhai, M. J. Roshtkhari, and G. Mori. Deep learning of appearance models for online object tracking. arXiv preprint arXiv:1607.02568, 2016.
49. Yang and R. Nevatia. Multi-target tracking by online learning of non-linear motion patterns and robust appearance models. In Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 1918–1925. IEEE, 2012.
50. Yang and R. Nevatia. An online learned crf model for multi-target tracking. In Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 2034–2041. IEEE, 2012.
51. Dicle, O. I. Camps, and M. Sznaier. The way they move: Tracking multiple targets with similar appearance. In Proceedings of the IEEE International Conference on Computer Vision, pages 2304–2311, 2013.
52. Helbing and P. Molnar. Social force model for pedestrian dy- namics. Physical review E, 51(5):4282, 1995.
53. M. Hu, S. Ali, and M. Shah. Detecting global motion patterns in complex videos. In Pattern Recognition, 2008. ICPR 2008. 19th International Conference on, pages 1–5. IEEE, 2008.
54. L. Wen, Z. Lei, S. Lyu, S. Z. Li, and M.-H. Yang. Exploiting hier-archical dense structures on hypergraphs for multi-object tracking. IEEE transactions on pattern analysis and machine intelligence, 38(10):1983–1996, 2016.
55. B. Zhan, D. N. Monekosso, P. Remagnino, S. A. Velastin, and L.-Q. Xu. Crowd analysis: a survey. Machine Vision and Applications, 19(5-6):345–357, 2008.
56. Solera, S. Calderara, E. Ristani, C. Tomasi, and R. Cucchiara. Tracking social groups within and across cameras. IEEE Transac- tions on Circuits and Systems for Video Technology.
57. X. Zhao, D. Gong, and G. Medioni. Tracking using motion patterns for very crowded scenes. In Computer Vision–ECCV 2012, pages 315–328. Springer, 2012.
58. P. Mordohai and G. Medioni. Dimensionality estimation, manifold learning and function approximation using tensor voting. Journal of Machine Learning Research, 11(Jan):411–450, 2010.
59. L. Kratz and K. Nishino. Tracking with local spatio-temporal motion patterns in extremely crowded scenes. In Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on, pages 693–700. IEEE, 2010.
60. L. Kratz and K. Nishino. Tracking pedestrians using local spatio-temporal motion patterns in extremely crowded scenes. IEEE transactions on pattern analysis and machine intelligence, 34(5):987–1002, 2012.
61. M. Rodriguez, S. Ali, and T. Kanade. Tracking in unstructured crowded scenes. In 2009 IEEE 12th International Conference on Computer Vision, pages 1389–1396. IEEE, 2009.
62. E. Ristani and C. Tomasi. Tracking multiple people online and in real time. In Asian Conference on Computer Vision, pages 444–459. Springer, 2014.
63. X. Wang, Intelligent multi-camera video surveillance: a review, Pattern Recognit. Lett. 34 (1) (2013) 3–19.
64. J. Candamo, M. Shreve, D.B. Goldgof, D.B. Sapper, R. Kas- turi, Understanding transit scenes: a survey on human behavior- recognition algorithms, IEEE Trans. Intell. Transp. Syst. 11 (1) (2010) 206–224.
65. B. Zhan, D.N. Monekosso, P. Remagnino, S.A. Velastin, L.-Q.Xu, Crowd analysis: a survey, Mach. Vis. Appl. 19 (5–6) (2008) 345–357.
66. I.S. Kim, H.S. Choi, K.M. Yi, J.Y. Choi, S.G. Kong, Intelligent visual surveillance-a survey, Int. J. Control. Autom. Syst. 8 (5) (2010) 926–939.
67. D.A. Forsyth, O. Arikan, L. Ikemoto, J. O’Brien, D. Ramanan, et al., Computational studies of human motion: part 1, tracking and motion synthesis, Found. Trends Comput. Graph. Vis. 1 (2–3) (2006) 77–254.
68. Yilmaz, O. Javed, M. Shah, Object tracking: a survey, ACM Comput. Surv. 38 (4) (2006) 13.
69. X. Li, W. Hu, C. Shen, Z. Zhang, A. Dick, A.V.D. Hengel, A survey of appearance models in visual object tracking, ACM Trans. Intell. Syst. Technol. 4 (4) (2013) 58.
70. Y. Wu, J. Lim, M.-H. Yang, Online object tracking: a benchmark, in: Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recog- nit., Anchorage, AL, USA, 2013, pp. 2411–2418.
71. L. Leal-Taix´e, A. Milan, I. Reid, S. Roth, K. Schindler, MOTChal- lenge 2015: towards a benchmark for multi-target tracking, arXiv:1504.01942, http:// arxiv.org/abs/1504.01942.
72. Z.-Q. Zhao, P. Zheng, S.-t. Xu, X. Wu, Object detection with deep learning: a review, IEEE Trans. Neural Netw. Learn. Syst. 30 (11) (2019) 3212–3232.
73. L. Wen, D. Du, S. Li, X. Bian, and S. Lyu, “Learning nonuniform hypergraph for multi object tracking,” arXiv preprint arXiv:1812.03621, 2018.
74. Sheng, Y. Zhang, J. Chen, Z. Xiong, and J. Zhang, “Hetero- geneous association graph fusion for target association in multiple object tracking,” IEEE Transactions on Circuits and Systems for Video Technology, 2018.
75. S. Ren, K. He, R. Girshick, and J. Sun, “Faster R-CNN: To- wards Real-Time Object Detection with Region Proposal Net- works,” IEEE TPAMI, vol. 39, no. 6, pp. 1137–1149, 2017.
76. D. Impiombato, S. Giarrusso, T. Mineo, O. Catalano, C. Gargano, G. La Rosa, F. Russo, G. Sottile, S. Billotta, G. Bonanno, S. Garozzo, A. Grillo, D. Marano, and G. Romeo, “You Only Look Once: Unified, Real-Time Object Detection Joseph,” Nuclear In- struments and Methods in Physics Research, Section A: Accelera- tors, Spectrometers, Detectors and Associated Equipment, vol. 794, pp. 185–192, 2015.
77. J. Redmon and A. Farhadi, “YOLO9000: Better, Faster, Stronger,” 2016.
78. P. Felzenszwalb, D. McAllester, and D. Ramanan, “A discrimina- tively trained, multiscale, deformable part model,” in Proc. CVPR, 2008.
79. K. Shafique and M. Shah, “A noniterative greedy algorithm for multiframe point correspondence,” IEEE transactions on pattern analysis and machine intelligence, vol. 27, no. 1, pp. 51–65, 2005.
80. D. Reid et al., “An algorithm for tracking multiple targets,” IEEE transactions on Automatic Control, vol. 24, no. 6, pp. 843–854, 1979.
81. Shu, A. Dehghan, O. Oreifej, E. Hand, and M. Shah, “Part- based multiple-person tracking with partial occlusion handling,” in Proc. CVPR. IEEE, 2012, pp. 1815–1821.
82. Roshan Zamir, A. Dehghan, and M. Shah, “GMCP-tracker: Global multi-object tracking using generalized minimum clique graphs,” in Lecture Notes in Computer Science, 2012.
83. Wu and R. Nevatia, “Detection and tracking of multiple, par- tially occluded humans by bayesian combination of edgelet based part detectors,” International Journal of Computer Vision, vol. 75, no. 2, pp. 247–266, 2007.
84. Dehghan, S. Modiri Assari, and M. Shah, “Gmmcp tracker: Globally optimal generalized maximum multi clique problem for multiple object tracking,” in Proc. CVPR, 2015, pp. 4091 4099.
85. Pirsiavash, D. Ramanan, and C. C. Fowlkes, “Globally-optimal greedy algorithms for tracking a variable number of objects,” Proc. CVPR, pp. 1201–1208, 2011.
86. A. Butt and R. T. Collins, “Multi-target tracking by lagrangian relaxation to min-cost network flow,” in Proc. CVPR, 2013, pp. 1846–1853.
87. Berclaz, F. Fleuret, E. Turetken, and P. Fua, “Multiple ob- ¨ ject tracking using k shortest paths optimization,” IEEE TPAMI, vol. 33, no. 9, pp. 1806–1819, 2011.
88. H. B. Shitrit, J. Berclaz, F. Fleuret, and P. Fua, “Multi-commodity network flow for tracking multiple people,” IEEE TPAMI, vol. 36, no. 8, pp. 1614–1627, 2014.
89. Leibe, K. Schindler, N. Cornelis, and L. Van Gool. Coupled ob- ject detection and tracking from static cameras and moving vehi- cles. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 30(10):1683–1698, 2008.
90. Milan, S. Roth, and K. Schindler. Continuous energy minimiza- tion for multitarget tracking. IEEE transactions on pattern analysis and machine intelligence, 36(1):58–72, 2014.
91. Shafique, M. W. Lee, and N. Haering. A rank constrained con- tinuous formulation of multi-frame multi-target tracking problem. In Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on, pages 1–8. IEEE, 2008.
92. Q. Yu, G. Medioni, and I. Cohen. Multiple target tracking using spatio-temporal markov chain monte carlo data association. In 2007 IEEE Conference on Computer Vision and Pattern Recognition, pages 1–8. IEEE, 2007.
93. S. Oron, A. Bar-Hille, and S. Avidan. Extended lucaskanade track- ing. In European Conference on Computer Vision, pages 142–156. Springer, 2014.
94. Yilmaz, Alper, Omar Javed, and Mubarak Shah.” Object tracking: A survey.” Acm computing surveys (CSUR) 38.4 (2006): 13-es.
95. McKenna, Stephen J., et al.” Tracking groups of people.” Computer vision and image understanding 80.1 (2000): 42-56.
96. Zhou, Xingyi, Vladlen Koltun, and Philipp Kr¨ahenbu¨hl.” Tracking objects as points.” Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part IV. Cham: Springer International Publishing, 2020.
FINANCING
The authors did not receive financing for the development of this research.
CONFLICT OF INTEREST
The authors declare that there is no conflict of interest.
AUTHORSHIP CONTRIBUTION
Conceptualization: Anass Ariss.
Data curation: Anass Ariss, Imane Ennejjai, Jamal Mabrouki, Soumia Ziti.
Formal analysis: Anass Ariss, Imane Ennejjai, Soumia Ziti.
Research: Anass Ariss, Imane Ennejjai, Jamal Mabrouki, Soumia Ziti, Nassim Kharmoum, Asmaa Lamjid
Methodology: Anass Ariss, Imane Ennejjai, Jamal Mabrouki, Soumia Ziti.
Supervision: Anass Ariss, Soumia Ziti.
Validation: Anass Ariss, Soumia Ziti.
Drafting - original draft: Anass Ariss, Imane Ennejjai.
Writing - proofreading and editing: Anass Ariss, Jamal Mabrouki, Soumia Ziti.