doi: 10.56294/dm2024.406

ORIGINAL

Optimizing a Novel Tracking System for Living Beings and Objects through Advanced Mathematical Modeling and Graph Theory

Optimización de un novedoso sistema de seguimiento de seres vivos y objetos mediante modelización matemática avanzada y teoría de grafos

Anass Ariss¹ *, Imane Ennejjai¹ *, Jamal Mabrouki² *, Soumia Ziti¹ *

¹Department of Computer Science, Faculty of Sciences, Mohammed V University in Rabat. Rabat 10000, Morocco.

²Laboratory of Spectroscopy, Molecular Modelling, Materials, Nanomaterial, Water and Environment, CERNE2D, Mohammed V, University in Rabat, Faculty of Science. Rabat, Morocco.

Cite as: Anass A, Imane E, Mabrouki J, Ziti S. Optimizing a Novel Tracking System for Living Beings and Objects through Advanced Mathematical Modeling and Graph Theory. Data and Metadata . 2024; 3:.406. https://doi.org/10.56294/dm2024.406

Submitted: 15-02-2024                   Revised: 29-05-2024                  Accepted: 17-09-2024                 Published: 18-09-2024

Editor: Adrian Alejandro Vitón Castillo

Corresponding Author: Anass Ariss *

ABSTRACT

This study extends the formulation of a tracking system for both live items and living persons, and gives a thorough theoretical framework for an advanced tracking system. A large number of tracking systems in use today were created inside certain frameworks and designed to monitor in either infinite or restricted spatial contexts. The latter typically makes use of specialized technological instruments designed with tracking objects or living things in mind. Our contribution to this topic is the formulation of a system theory that both formulates and innovates the challenge of monitoring objects and living things. Graphical modeling is widely used in tracking, which is interesting because it makes it easier to create precise relationships between the objects that need to be tracked and other parts of the system. But our study argues that the best way to achieve a high-performing, contextually relevant, and flexible system in a range of scenarios is still to build a tracking system around graphs, both theoretically and practically. We provide a unique tracking method to further the discipline, based on the ideas of hypergraphs and graph learning. This method carefully examines the order between various linkages inside the system, allowing the system to fully use both direct and indirect relations. The way we formulate tracking is as a complex search problem on graphs and hypergraphs. In this case, the system’s components—living things or objects—are represented by vertices, and the kinds of relationships that exist between them are indicated by edges. We present a governing law that facilitates different processing tasks, manages shared data across system parts, and defines the connections between vertices. Additionally, we provide illustrated examples covering single and multi-context tracking scenarios to support our work. These illustrations highlight how, in comparison to current tracking technologies, the suggested approach performs better theoretically. In addition to adding to the theoretical conversation, this discovery has potential applicability in a variety of tracking contexts.

Keywords: Tracking System; Tracking; Graph Learning; Hypergraph.

RESUMEN

En este artículo, ampliamos la formulación de un sistema de seguimiento diseñado tanto para objetos como para seres vivos. También proporciona un marco teórico completo para un sistema de seguimiento sofisticado. Muchos sistemas de seguimiento actuales se crean con frecuencia dentro de marcos específicos, diseñados para operar en escenarios espaciales limitados o ilimitados. Estos últimos generalmente utilizan herramientas técnicas específicas para monitorear objetos u seres vivos. Nuestra contribución a este estudio se basa en la propuesta de una teoría de sistemas que no solo desarrolla, sino que también innova la tarea de rastrear objetos y seres vivos. En el campo del rastreo, el modelado gráfico es muy utilizado porque facilita la creación de conexiones precisas entre los elementos a rastrear y otros componentes del sistema. Sin embargo, nuestra investigación muestra que la mejor manera de lograr un sistema de alto rendimiento, contextualmente relevante y adaptable en una variedad de situaciones es usar un sistema de seguimiento basado en grafos, tanto en sus fundamentos teóricos como en su aplicación práctica. Presentamos un novedoso sistema de seguimiento basado en los principios del aprendizaje de grafos y hipergrafos para avanzar en este campo. Con esta estrategia, el sistema puede maximizar las relaciones directas e indirectas, al mismo tiempo que examina minuciosamente el orden de las múltiples conexiones que forman parte del sistema. El seguimiento se conceptualiza en nuestra formulación como un complicado problema de búsqueda en grafos e hipergrafos. Aquí, los elementos del sistema (seres vivos u objetos) se representan por vértices y las aristas delinean los tipos de conexiones entre ellos. Introducimos una ley rectora que establece las relaciones entre vértices, administra los datos compartidos entre los componentes del sistema y facilita una variedad de tareas de procesamiento. Además, nuestro trabajo se basa en ejemplos claros que abarcan situaciones de seguimiento en una variedad de contextos. Estos ejemplos demuestran la superioridad del rendimiento teórico del sistema propuesto en comparación con los sistemas de seguimiento actuales. Esta investigación no solo amplía el discurso teórico, sino que también tiene aplicaciones prácticas en una variedad de escenarios de seguimiento.

Palabras clave: Sistema de Seguimiento; Seguimiento; Aprendizaje de Grafos; Hipergrafo.

INTRODUCTION

Hallinan⁽¹⁾ are now very interested in developing an efficient tracking system, especially in light of recent events like the COVID-19 pandemic. It is difficult to design a system that can monitor a variety of objects, including live things. This is because it requires predicting behaviors,⁽⁴⁾ trajectories,⁽³⁾ and other complex variables. One way to think about the learning problem in tracking systems⁽¹⁾ is as the formation of a multipartite graph, where nodes and multipartite edges (hypergraph) link to each other,⁽⁵⁾ creating a complicated web of interactions. The final goal is to create a model that can fully represent the data that is included in this graph. For tracking popular occurrences like epidemics, a tracking system is an essential tool. This kind of monitoring has to be scalable, accurate, and efficient. In this work, we want to design a general-purpose and flexible system that can handle a variety of circumstances by smoothly going down to a lower level of detail. Our main goal is to create a tracking system that can identify possible dangers in the setting of this complex issue. In order to provide a complete traceability system, this system should guarantee the traceability of both items and living things. The system has to be flexible enough to monitor several sorts of prototypes, such as COVID-19, abduction, terrorism, etc. An essential part of this system’s design is taking into account the preset prototypes and their measurements. The application of the technology will be limited to an infinitely large predetermined geographic area.⁽⁶⁾ Its architecture will resemble a hypergraph,⁽⁵⁾ allowing nodes to communicate in a variety of settings. An optimization problem will be formed by the activation of various contexts, which will be controlled by a function with several variables, each of which is produced by mathematical principles. Relationships between nodes are defined using this function, which can be shared by several nodes. This study defines the fundamental premise of our system in a groundbreaking manner. It is intended to carry out complex modeling among several monitored element kinds, improving the understanding of their properties to understand both their present state and future behavior. Our methodology extends the reach of conventional tracking techniques by integrating a flexible and dynamic framework that may change as the monitored items change. To facilitate a deeper understanding, our system introduces the concept of a matrix to model the connections between nodes. Each matrix is defined by the number of connections between a pair of nodes, serving as variables for the function that models the various contexts. This innovative methodology represents a novel contribution to the field, providing a comprehensive and systematic approach to tracking system design. Our system not only addresses the immediate challenges posed by tracking living beings and objects but also lays the groundwork for a transformative paradigm in tracking system design. By combining mathematical principles, hypergraph modeling, and contextual optimization, we aim to contribute to the development of a highly efficient, adaptable, and future-ready tracking system.

Figure 1. Multi-context tracking system modeling

Initial steps

Clarification and Definitions

Tracking

Tracking is the active process of continuously monitoring and determining the status of objects, encompassing living beings, and assessing the position or movement of an object or living being at a specific moment or over an extended period. This multifaceted task can be achieved through a spectrum of methods, ranging from traditional approaches grounded in simple theories to the sophisticated integration of state-of-the-art technologies. The applications of tracking are wide-ranging and span diverse fields, including logistics, geolocation, surveillance, counter-terrorism, and epidemiology. The following discourse offers an in-depth exploration of tracking, delving into its historical evolution, fundamental concepts, and versatile applications.⁽¹⁾

The historical roots of tracking⁽¹⁾ extend deep into antiquity, where human reliance on footprints, animal tracks, and other environmental cues enabled the tracking of prey and adversaries alike. Over successive centuries, tracking techniques underwent significant refinement, finding application in various domains such as navigation, wildlife monitoring, and criminal investigations. The foundational principles of tracking involve the systematic identification of the object or living being to be tracked, the meticulous measurement of its movement, and the precise calculation of its location. Diverse techniques are employed to accomplish these tasks, each catering to specific tracking scenarios:

• Tracking by signs: this method relies on the identification and interpretation of signs left by the object or person being tracked, such as footprints, tire tracks, or DNA evidence. Practitioners of sign tracking leverage their expertise in both the environment and the behavior of the target to locate and interpret these signs effectively.

• Electronic tracking: in the realm of electronic tracking, cutting-edge devices such as GPS, RFID, and Bluetooth beacons are employed to locate and monitor the movement of objects, vehicles, and individuals. Emitting signals that can be precisely detected, these electronic devices facilitate the accurate calculation of the location of the tracked object or person.

• Visual tracking: visual tracking involves the deployment of cameras and other visual sensors to monitor the movement of objects and individuals. Visual tracking systems leverage advanced computer vision techniques to analyze images and provide real-time tracking capabilities.

The applications of tracking extend across diverse fields, demonstrating its versatility and adaptability. Here are a few illustrative examples: 

• Wildlife tracking: tracking plays a pivotal role in observing the movement and behavior of animals in their natural habitats. This wealth of information is indispensable for ecological studies, understanding migration patterns, and unraveling social behaviors within animal populations.

• Criminal investigations: law enforcement agencies employ tracking techniques to locate and monitor suspects, fugitives, and missing persons. Furthermore, tracking is instrumental in the collection of evidence for criminal cases, enabling investigators to trace a suspect’s movements before and after the commission of a crime.

• Transportation: tracking systems are integral to monitoring the movement of vehicles, including trucks, ships, and airplanes. These systems play a crucial role in enhancing route optimization, logistics management, and overall security within the transportation sector.

Tracking System

A tracking system, with its ability to monitor various aspects such as position, speed, behavior, and even the health of living beings, serves as a dynamic tool with diverse applications. This adaptability extends across numerous fields, encompassing critical areas such as epidemics, counter-terrorism, kidnapping prevention, and beyond. Grounded in theoretical frameworks like graph theory, these systems seamlessly integrate sophisticated technical equipment for practical implementation. The following section delves deeper into tracking systems, exploring their historical evolution, foundational principles, and the expansive scope of their applications.

Originating during the Second World War, tracking systems emerged as a groundbreaking solution for monitoring and locating enemy aircraft. Early implementations relied on radar technology to detect the presence and movements of aircraft. Over subsequent decades, these systems evolved, finding applications in diverse realms, from navigation and wildlife tracking to logistical operations. Fundamental to a tracking system are three core components: a transmitter affixed to the target or individual, a receiver capturing emitted signals, and a processing unit that analyzes the signals to determine the subject’s location.

The technologies employed by tracking systems for signal transmission and reception are diverse, each catering to specific needs. Notable examples include:

• The Global Positioning System (GPS): utilizing a network of satellites, the GPS satellite tracking system transmits signals to ground-based GPS receivers. These receivers triangulate signals from at least four satellites to determine precise location coordinates.

• Radio frequency identification (RFID): RFID, utilizing radio waves, facilitates the identification and tracking of individuals or objects. RFID tags, attached to items or individuals, emit signals picked up by RFID readers.

• Bluetooth Low Energy (BLE): this wireless communication technology is integral for indoor positioning in tracking systems. BLE beacons strategically placed emit signals that smartphones or devices equipped with BLE receivers leverage to determine their precise location.

The applications of tracking systems span a multitude of industries, showcasing their versatility and significance. Consider the following examples: 

• Transportation: in the transportation sector, tracking systems monitor the movement and location of vehicles, including trucks, ships, and airplanes. This real-time information is indispensable for logistics management, enhancing security protocols, and optimizing travel routes for efficiency.

• Logistics: tracking systems play a pivotal role in monitoring the flow of goods across intricate supply chains. These systems contribute to effective shipment management, inventory tracking, and overall operational efficiency.

• Security: within security and law enforcement, tracking systems are invaluable tools for locating and monitoring suspects, runaways, and missing persons. They also serve a crucial role in asset tracking, preventing theft, and safeguarding valuable items.

In conclusion, tracking systems are dynamic and multifaceted solutions that continue to evolve, offering innovative applications across a spectrum of industries, ultimately contributing to enhanced efficiency, security, and operational effectiveness.

Graph Theory

The Far-reaching Impact of Graph Theory

Graph theory,^{(7,8,9,10,11)} with its roots traced back to Euler and Hamilton’s pioneering work in the 18th century, stands as a foundational mathematical tool with extensive applications. At its essence, a graph G represented as (V,E)^{(5,7,8,9,10,11,12)} succinctly captures relationships between entities. Its adaptability in modeling diverse scenarios, from transportation networks to intricate social connections, positions graph theory as a central element in effective problem-solving across various domains.

Realizing Abstract Representations

Within the sphere of information technology, graph theory^(9,12) finds concrete expression in data structures like trees, graphs, and linked lists. Algorithms grounded in graph theory principles play a pivotal role in solving complex problems, including determining the shortest paths, optimizing network traffic, and addressing correspondence challenges across diverse applications. By abstracting real-world scenarios into nodes and edges, graph theory becomes a potent abstraction tool, facilitating a deeper comprehension of intricate relationships.

Analyzing Social Networks

In the social sciences, graph theory takes center stage in network analysis. Researchers harness the power of graphs to dissect the intricate structure and dynamic nature of social networks. By modeling individuals, groups, and organizations as nodes interconnected by edges, analysts can simulate interactions, pinpoint influential nodes, and gain insights into the nuanced dynamics of social relationships. This application extends into sociology, anthropology, and psychology, enriching our understanding of human behavior and societal structures.

Optimizing Operational Processes

Operational research benefits significantly from graph theory, particularly in optimization problems. The classic example of the traveling salesman problem illustrates how graphs assist in finding the most efficient route between a set of cities and the starting point. This optimization extends to logistics, resource allocation, and supply chain management, where graph-based algorithms contribute to streamlined and cost-effective operational processes.

Beyond Graphs: The Rise of Hypergraphs

Expanding our exploration leads us to the evolution of graphs into hypergraphs. Going beyond the binary connections of graphs, hypergraphs offer a more nuanced representation, enabling connections between more than two vertices. This generalization proves invaluable across various disciplines.

Characteristics and Applications of Hypergraphs

Hypergraphs, denoted as H(V,E), redefine the conventional edges of graphs. A hyperedge, a subset of vertices, can connect any number of vertices, introducing a novel layer of complexity. This characteristic becomes particularly pronounced in ’uniform’ hypergraphs, where all hyperedges share the same size, and ’non-uniform’ hypergraphs, allowing variability. The hyperdegree of vertices, measuring their connection to hyperedges, and the hyperdegree of hyperedges, reflecting the number of vertices they encompass, add further dimensions to the study of hypergraphs.

Practical Applications Across Disciplines

The applications of hypergraphs span a wide array of fields. In computer science, hypergraphs shine in data clustering algorithms, where each hyperedge represents a distinct cluster of data points. Physicists leverage hypergraphs to study complex systems, where hyperedges symbolize groups of interacting particles, pushing the boundaries of our understanding of physical phenomena. In the social sciences, hypergraphs in network analysis capture groups of individuals with shared characteristics, offering a nuanced perspective on societal structures and dynamics.

As we delve into prevalent operations performed on hypergraphs, it becomes evident that the extension from graphs to hypergraphs enhances our capacity to model and analyze complex relationships in diverse contexts. The continued exploration of hypergraphs promises to unlock new dimensions in data representation, analysis, and problem-solving, contributing to advancements across computing, physics, social sciences, and beyond.

Usefulness of Graph Theory in Tracking Systems

Integrating graph theory^(10,14) into tracking systems is not merely a suggestion; it is a fundamental necessity. Graphs serve as dynamic and versatile tools for effectively representing the intricate components within a tracking system.⁽¹⁵⁾ These components, ranging from sensors to tracking objects, find a coherent visual representation within a graph, offering clarity on their interconnections and relationships. By embracing this approach, the door opens to the development of sophisticated tracking algorithms. Moreover, it provides a framework for insightful evaluations, allowing stakeholders to identify opportunities for enhancement by strategically modifying the graph structure.

Graph theory’s⁽⁹⁾ prowess extends beyond mere representation; it becomes a linchpin for understanding and analyzing the temporal movements of objects or individuals. Consider the scenario of modeling an individual’s movements post a positive COVID-19 diagnosis or the monitoring of child abductions. Here, graph theory excels by defining elements to be tracked as nodes and representing the contextual connections between these elements as edges. The application of graph algorithms becomes instrumental, enabling tasks such as finding the shortest path between nodes or identifying the most frequently visited locations for a tracked element.

Furthermore, graphs unfold as powerful visualizations of the intricate relationships that weave through a tracking system. Whether elucidating the diverse fields of application for tracking an object or person or depicting the multifaceted data collected by the system,^(80,92) graphs become indispensable storytellers. Their visual narrative aids in unraveling the complex tapestry of interactions between elements. This comprehensive understanding, facilitated by graphs, becomes a cornerstone for refining and optimizing the operational dynamics of the tracking system.⁽¹³⁾

In essence, the marriage of graph theory and tracking systems transcends a mere integration; it becomes a synergy that empowers systems to not only monitor but comprehend and adapt in an ever-evolving landscape of dynamic information.

Categories of Tracking Systems

The myriads of tracking systems available share a common overarching goal to evaluate and quantify the effectiveness, precision, and reliability unique to each system type. However, the outcomes of these assessments are contingent upon several variables, including the specific application, prevailing environmental conditions, and the requisite level of precision. Much like any technological innovation, tracking systems exhibit both advantages and disadvantages, and the crux lies in identifying the most fitting system to address particular needs. A comprehensive comparison involves evaluating factors such as precision, dependability, user-friendliness, cost-effectiveness, and adaptability.

These tracking systems can be systematically categorized based on their data collection and analysis capabilities into four distinct types:

• Localization Tracking Systems: these systems are dedicated to tracking and mapping the position and movement of physical entities. They find applications in scenarios where spatial awareness is paramount, such as navigation and logistics.⁽⁸⁸⁾

• Tracking Systems for Activities: falling under this category are systems specifically designed to track and record the activities of both physical and virtual entities. This type of tracking is invaluable in contexts ranging from sports performance analysis to user engagement tracking in virtual environments.⁽⁸⁰⁾

• Performance Tracking Systems: tailored to monitor and measure the performance of physical or virtual entities, these systems provide valuable insights into how well an entity is fulfilling its intended function. This can be particularly crucial in fields like manufacturing, where efficiency and output are paramount.⁽⁸¹⁾

• Data Tracking Systems: positioned at the intersection of tracking and analytics, these systems are geared toward tracking and analyzing data generated by physical or virtual entities. They play a pivotal role in sectors such as data-driven decision-making, where understanding and leveraging data patterns are essential.⁽¹⁸⁾

In navigating the landscape of tracking technologies, a nuanced understanding of these categories becomes instrumental in selecting the most suitable system based on the specific demands of the application at hand. Each category brings a unique set of capabilities to the forefront, and discerning their nuances enables users to make informed choices tailored to their objectives and operational requirements. The Preliminaries section lays the groundwork for a systematic and reliable exploration of evaluating the reliability of graph theory within tracking systems, a pivotal factor comes to the forefront the quality of the data utilized. The efficacy of graph theory hinges on the precision and completeness of the data employed to model a tracking system. When armed with accurate and comprehensive data, graph theory becomes an indispensable tool, offering profound insights into the inner workings of the system and furnishing effective solutions to intricate problems. Graph theory excels in providing a visual and analytical framework for understanding relationships, dependencies, and patterns within a tracking system. By representing elements as nodes and their connections as edges, it allows for a nuanced analysis of the intricate web of interactions. This proves particularly beneficial when optimizing routes, predicting movements, or discerning patterns of behavior. Conversely, the Achilles’ heel of graph theory surfaces when confronted with incomplete or inaccurate data. In such scenarios, the reliability of the results obtained diminishes significantly. The inherent strength of graph theory lies in its ability to draw meaningful conclusions based on the information it processes. When the input data are flawed, the output is compromised, potentially leading to misguided interpretations and decisions.⁽⁹⁷⁾ Therefore, the success of leveraging graph theory in tracking systems is contingent upon a conscientious approach to data quality. Rigorous efforts to ensure data precision and completeness lay the foundation for harnessing the full potential of graph theory. As we navigate the intricate realm of tracking technologies⁽⁹⁸⁾ a mindful acknowledgment of this symbiotic relationship between data quality and the reliability of graph theory becomes paramount.

Related work

Tracking systems based on graph theory involve the representation of visual data as graphs, where peaks correspond to pixels, superpixels, or object parts, and valleys indicate hyperedges connecting the nodes. This graph structure is leveraged to predict labels for non-tagged peaks, making it a powerful tool in various computer vision tasks. Notably, graph-based algorithms have demonstrated success in object detection⁽¹⁹⁾, recognizing human activities⁽²⁰⁾, and facial recognition.⁽²¹⁾ Traditionally, trackers using graphs adopt superpixels as nodes to represent the appearance of objects, while edges encode the internal geometric structure. Another strategy involves constructing graphs between different parts of objects in various images. This approach has led to the development of diverse trackers.^{(6,22,23,24,25)} In recent years, tracking has evolved to handle multi-target scenarios.^(26,27,28) Multi-target tracking (MTT) goes beyond appearance models, recognizing that relying solely on appearances can be problematic in cluttered scenes or when targets share similar appearances. Consequently, research has focused on improving appearance models⁽²⁹⁾ and combining target and non-target appearances.^{(3,30,31,32,33,34,35)} Simplistic models are often used in MTT, including those based on raw bitmap representations.^{(32,33,36,37,38)} Color histograms are popular for appearance modeling in MTT.^(34,39,40) Additionally, other approaches leverage covariance matrix representations, pixel comparisons, SIFT characteristics, or pose characteristics.^{(41,42,43,44,45)} Recently, deep neural network architectures have been employed for perception modeling^(46,47,48) extracting high-level features through convolutional neural networks. The movement model of a target is a critical aspect of MTT, describing how the target moves between frames. Commonly used movement models include linear and nonlinear models. Linear models assume constant speed, while nonlinear models offer more precise predictions.^(52,53,54) Assuming independent movement patterns for each target simplifies tracking techniques but may be problematic in complex scenes. Interaction models that capture forces and interactions between different targets have been proposed.^(22,25,39) Notable examples include the social force model⁽²²⁾ and the mass movement model.⁽²⁵⁾ In these models, each target responds to potential energy sources generated by force interactions with other objects while maintaining a desired speed and direction.^{(56,57,58,59,60,61,62)} Mass movement models, inspired by mass simulation, are used in entangled scenes.^(55,56) A recent advancement by Arahi et al.⁽³¹⁾ proposes using long short-term memory networks (LSTM social) for reasoning with multiple people, providing a framework for forecasting long-term trajectories for all targets. While a comprehensive review of literature on tracking multiple objects is lacking, related studies can be categorized into four groups:

• The first series^{(4,63,64,65,66)} treats object tracking as an individual component. In contrast, this work specifically addresses various elements of tracking multiple objects. For instance, object tracking is considered a step in high-level tasks like foul model simulation.^(4,65,66) Object following is examined in^(63,64) for behavior recognition⁽⁶⁴⁾ or video surveillance.⁽⁶³⁾

• The second series^(67,69) explores general visual tracking approaches^(67,68) or specific problems like models of appearance in visual tracking.⁽⁶⁹⁾ However, their scope extends beyond ours, concentrating on tracking numerous objects.

• The third series^(70,71) discusses benchmarks for visual object tracking⁽⁷⁰⁾ and multi-object tracking⁽⁷¹⁾ focusing on experimental studies instead of literary reviews.

• The fourth series⁽⁷²⁾ reviews recent advancements in object detection through deep learning. While related, object detection differs from multi-object tracking (MOT), which combines data over multiple photos to generate object trajectories.

Several systems for tracking multiple objects adopt the tracking-by-detection framework.^(18,73,74) In this context, objects are first identified and then linked across various photographs. With advancements in multiple object detectors^{(75,76,77,78)} these strategies emphasize data association and can be categorized into local and global monitoring methods. Local methods^(79,80,81) consider associations between two photos, offering computational efficiency but sensitivity to irrelevant factors. In contrast, global strategies^(82,83,84) use a larger number of images, often treating data association as a network flow problem.^{(85,86,87,88)}

Figure 2. Context-separated tracking system modeling

Problem formulation

The nature of connections, or the establishment of inter-node links, is intricately defined by the governing Ψ law. This is exemplified in figure 1, illustrating the modeling of a multi-context tracking system. This model accommodates the presence of zero or multiple context-type relationships between nodes, including both direct and indirect connections. The conceptual framework is grounded in the principles of hypergraphs, providing a versatile structure for capturing complex relationships within the tracking system. The adaptability of each node to interact across diverse contexts is a fundamental aspect of the proposed model. Figure 2 extends this concept by illustrating a tracking system with separate contexts. In this configuration, each node can have one or more clones, or duplicates, across different context clouds. This results in the existence of several context graphs for a given hypergraph, offering a nuanced representation of the system’s interconnectedness. In the context-driven dynamics, each node is endowed with the ability to have a dynamic clone based on the specific context it operates within. This dynamic nature allows nodes to exhibit varying behaviors and characteristics, enhancing the system’s adaptability to changing conditions. The inherent connection between a node and its clones is a pivotal aspect of the model. This linkage ensures coherence and consistency in the information shared across different contexts, promoting a unified representation of each node’s attributes. The metric employed to characterize the connections between nodes may vary across different pairs within the system. This introduces flexibility in defining relationships, acknowledging that certain pairs may exhibit fewer contextual dependencies than others. The system’s capacity for contextual richness is quantified by the maximum number of contexts that can exist between pairs of nodes. This contextual diversity contributes to the system’s adaptability and nuanced representation of relationships. The data representation for each node is structured in a hierarchical order: public, neighborhood, and private. This hierarchical organization aids in managing the accessibility and visibility of information based on contextual relevance. During this modeling stage, the shared data structure between nodes is temporarily de-emphasized, allowing for a focus on individual nodes and their contextual interactions. The relationship dynamics between each pair of nodes can be infinite, reflecting the complex and multifaceted nature of interactions within the system. Characteristic updates occur when a node’s clone transitions between environments, prompting essential questions for effective management. Which parameters, such as context, should be activated in each environment? What parameters are universally shared across all environments? How are these parameters managed, and what rules govern their definition?

The movement of a node from one environment to another triggers a metric, raising the critical question. How can the system reliably detect that a node has changed its environment?

Figure 3. Representation of a tracking system with a single context

Once a node’s change of environment is confirmed, a trigger initiates a dynamic update of the node’s profile, rendering the system dynamically responsive to environmental shifts. The concept of zones and sub-zones, interconnected through shared contextual data, enhances the system’s organizational structure. This contextual zoning facilitates effective communication and information exchange between different parts of the tracking system. Comprehensive records of the directional attributes of all nodes are essential for maintaining accurate and efficient tracking. A systematic registration of node directions in a structured format ensures the precision of tracking operations. To ensure a comprehensive understanding of the system’s dynamics, a thorough knowledge of all node contexts is necessary. This includes consideration of both previous and current contexts, contributing to a holistic view of the system’s evolution. Communication methodologies and data types play a pivotal role in shaping the system’s interactions. Consideration of communication channels (e.g., mail, IoT) and data types (structured, unstructured) becomes crucial and will be further processed in a subsequent data preprocessing layer. Each node in the tracking system is endowed with specific communication characteristics, influencing how information is exchanged. For instance, the common ground between individuals X, Y, and Z may revolve around the context of scientific research. This context can be communicated through various means, either directly or indirectly, as depicted in figure 3. This illustrates a modeling scenario of a single-context tracking subsystem, where one or more nodes may participate in other subsystems concurrently.

Comprehensive analysis of robustness and proposal for a systematic approach

In a tracking system, two scenarios must be considered: the oriented system figure. 4 and the non-oriented system figure 3. We have given close attention to the case of an orientated tracking system during this research.

Foundational Concepts in Tracking Systems

In a tracking system, two situations need to be considered, that of an oriented system and that of a non-oriented system, as shown in figure 5.

T_s=〈V,E,δ,Ψ,I^-,I⁺〉

I^-: V×E↦∑(x_i,x_j)∈Vⁿ Σ(x_i,x_j); (x_i≠ x_j i≠j)

Where:

V: “Nodes” are a set of vertices.

E: “Link” is a set of edges.

δ:E⟶V×V/{{x,y}|(x,y)∈V²∧x≠y}. An incidence function that links a pair of vertices to every edge. 

Ψ: Delta Tracking Law (DTL). The law of direct relationship that exists between the system’s components is specified by legislation.

I^-: V×E↦∑(x_i,x_j)∈Vⁿ Σ(x_i,x_j); (x_i≠ x_j i≠j). is how the earlier nodes were applied.

I⁺: V×E↦∑(x_i,x_j)∈Vⁿ Σ(x_i,x_j); (x_i≠ x_j i≠j). is the following nodes’ application.

We also incorporate the concept:

I=I⁺-I^-  and I is referred to as the system’s impact matrix.

System with Contextual Integration

An ensemble of interconnected elements in a contextual tracking system consists of:

∑=<T_s,Ctx>

Where:

T_s constitutes the tracking system.

Ctx represents the initial context, serving as an application.

Ctx:V↦δ

Ctx(V) signifies the number of contexts within the node V, these encompass the diverse contexts that a node can possess.

Tracking System and Matrix Concepts in Association

We can link a tracking system to a hypergraph where nodes may assume various forms based on the contexts to which they belong. A node is connected to a DTL law by one or more arcs if and only if I^- (v,ψ)≠0. Similarly, a DTL law is linked to a node by one or more arcs if and only if I⁺ (v,ψ)≠0. The non-zero values in the matrices I^- and I⁺ serve as labels for the arcs (by default, they take on the values of context IDs).

All tracking systems exhibit perfection

A focused tracking mechanism T_s is considered perfect if and when:

The system does not contain any elementary loop, meaning that no  law has the same node as both input and output.

Figure 4. Modeling a maximum of three contexts for an orientated tracking system

Signage

The signaling, denoted as S, represents the data (neighborhood, public) that a node can propagate or share with the external environment. This signaling can be represented as a multi-dimensional vector with a length equal to the number of contexts associated with the node. The system is considered in two directions for the edges E, and we define the first direction based on the initial context. The matrices I^-, I⁺, and I have several rows equal to the number of vertices and several columns equal to the number of DTL laws.

Figure 5. Modeling a tracking system that is non-oriented and may have up to three contexts

Let I^- (.,ψ), I⁺ (.,ψ) and I(.,ψ) denote the columns of these matrices associated with a ψ law. For instance, figure 4 illustrates a tracking system with a maximum of three contexts, featuring both direct and indirect relations, along with the tracking law defining the contextual relationships between system elements. The figure 4 also indicates the number of activated contexts for each pair of nodes, defined as follows:

We then have: 

The initial signage is: 

DS_i represents a data structure shared by the node based on its context. This data structure can encompass various types of publics, private and neighbor data from nodes with different contexts.

DTL traversable law

A Ψ law is considered traversable if and only if:

We can denote the traversability of ψ using the notations:

For example, in figure 4, depicting an oriented tracking system with initial signalization:

Where the components of S indicate the count of data structures DS_i corresponding to each context for every law ψ_i. The traversability of laws ψ₁ and ψ₃ is justified by: 

Transversal of a Ψ law

If ψ is traversable with respect to the signalization S, traversing ψ generates a new signaling S›, defined as:

For example, in the system of figure 4, we discuss the traversement of ψ₁ from the initial S signalization, so we get the following S’ signalization, defined as:

For instance, in the system illustrated in figure 4, let’s explore the traversal of ψ₁ from the initial S signalization, leading to the subsequent S’ signalization:

Conflict and parallelism

Structural conflict

Two DTLs, ψ_i and ψ_j, are structurally conflicting if and only if they share at least one vertex:

Effective conflict

For a given signaling S, two DTLs, ψ_i  and ψ_j, are effectively conflicting if and only if they are in structural conflict such that: 

Structural parallelism

Two DTLs, ψ_i and ψ_j, are structurally parallel if they have no common entry vertex (the scalar product of their I^- vectors are null):

Effective parallelism

For a given signalization S, two DTLs, ψ_i and ψ_j, are effectively parallel if and only if they are structurally parallel:

In the tracking system depicted in figure 4, laws ψ₁ and ψ₂ are structurally conflicting since:

On the other hand, laws ψ₅ and ψ₇ are structurally parallel. Indeed: 

For the initial signalization S, laws ψ₁ and ψ₂ are ineffective conflicts. If we now consider the signalization.

Let W ⃗ be the vector whose components represent the 0 values in S’ corresponding to vertices v₁ and v₆, indicating that they have no contexts to consider. This situation can be viewed as a contestable element. Then, laws ψ₅ and ψ₇ are effectively parallel (They are able to be traversed separately from one another).

Traversable sequence

S₀ →^ψ2 S₁ and S₁→^ψ4 S₂, we say that the sequence (ψ₂,ψ₄) is traversable from S₀, represented as:

Let W ⃗ be the vector whose components W ⃗(Ψ) represent the number of activations of Ψ laws (number of occurrences) in a traversal sequence S. The characteristic vector of this vector is S, with a dimension equal to the number of Ψ laws in the tracking system. Still considering the tracking system in figure 4, we have, for example, the sequence S=(ψ₂, ψ₂, ψ₃):

Assuming:

Where we simulate, this time, DS_i, the data structure shared among nodes, based on the quantity of contexts shared with the nodes.

The evolution of the signalizations in a tracking system is expressed by the fundamental equation I⋅S¯.

For our example:

In a specific scenario, the notion of generating signalization graphs is very intriguing. Depending on the application domain or context, there are several ways to interpret the concept of signalization graphs. A signalization graph, a graphical depiction in the form of a tree structure that highlights the data exchange between various tracking system components, could serve as a specific example. These graphs are critical to many industries, including computer science, artificial intelligence, financial markets, telecommunications, molecular biology, crisis management, terrorism, abduction and epidemics.

Utilizing these signalization graphs as visual aids to comprehend information flows, exchanges, or signals that impact decisions, each field interprets and applies them in a unique way. These graphs are proving to be very useful tools, whether we are discussing communication networks, biological processes, financial indicators, or robust tracking techniques for phenomena that directly affect society, like terrorism, kidnapping, or epidemics. Our tracking system might develop into an effective instrument for evaluating and improving a variety of intricate systems in this way. Signaling graphs can be constructed.

Here are some potential applications for this concept in various settings:

Telecommunications Network

Signalization graphs are graphical depictions of signaling flows between network nodes in the context of telecommunications. Signaling protocols like SIP (Session Initiation Protocol) in VoIP communications may fall under this category.

Molecular Biology

Signalization graphs, which illustrate how signaling molecules interact within cells to govern various biological processes, could be used in molecular biology to portray cellular signaling pathways.

Finance and Market Analysis

Signalization graphs in the financial realm could be signs or signals that affect investing choices. Graphs, for instance, could show how various financial indicators are correlated.

Computer Science and Distributed Systems

Signalization graphs are a term used in computer science to describe the visual depiction of signals exchanged among various distributed system components. Messages, occasions, or other kinds of communication between modules may fall under this category.

Machine Learning and Neural Networks

Signalization graphs may be used in machine learning to illustrate how signals go across a neural network’s layers. This could help to comprehend how data is handled and distributed within the model.

Terrorism

Signalization graphs can be used in the context of counterterrorism operations to examine communication and coordination patterns among suspected terrorist individuals or groups. Security authorities can identify possible dangers and take preemptive action to ensure public safety by mapping out the communication network.

Kidnappings

Signalization graphs can be used by law enforcement and security agencies to analyze and comprehend communication patterns associated with abduction cases. It can be helpful to follow and prevent kidnapping instances to analyze the network of communication among criminals, collaborators, and possible victims. This method aids in the creation of successful plans for law enforcement organizations.

Epidemics

Signalization graphs are essential for tracking the spread of epidemics in the realm of public health. Health authorities can predict and respond to the spread of infectious diseases by tracking travel patterns, evaluating communication networks, and modeling individual interactions. When it comes to putting containment measures into place and lessening the impact of epidemics on communities, signalization graphs offer invaluable information. It would be vital to provide more information for a deeper understanding and to steer the development of this notion in a specific direction, depending on the particular situation in which it is introduced.

Accessible signalization

The set of accessible signage, denoted as AS(T_s,S₀), for a signaled tracking system is defined as the collection of signalizations that can be attained from the initial signage S₀ through a traversal sequence. 

When the set of reachable signalizations is finite, it can be represented as a graph denoted as GAS(T_s, S₀). This graph has a vertex set corresponding to the set of accessible signages AS(T_s, S₀). A directed edge connects two vertices S_i and S_j if there exists a traversable DTL law that allows transitioning from one signage to another based on an activated context: S_i →^Ψ S_j. Typically, the edges of the graph are labeled with the corresponding context and the associated ψ_i law.

System of regulations and tracking system

Tracking System

In the first perspective, the tracking system is envisioned as a graph where various types of edges represent dynamic interactions. This graphical representation captures the complex relationships and dependencies between different elements within the system. In the second perspective, the tracking system is characterized as a set of matrices, and its dynamic behavior is mathematically described by the fundamental equation of the linear system. This formal representation provides a systematic way to analyze and understand the evolution of the system over time. In the third perspective, the tracking system is conceptualized as a knowledge production system, also referred to as a deduction system. This perspective involves a rule-based framework where the system’s behavior is governed by rules structured as:

Here, the system is triggered under certain conditions, leading to specific actions. This knowledge representation approach facilitates a comprehensive understanding of how the tracking system operates and responds to various stimuli. By examining the tracking system through these diverse lenses, we gain a holistic perspective that encompasses its graphical, mathematical, and knowledge-driven aspects.

System of regulations

Let’s delve deeper into the components and dynamics of a tracking system operating as a rule-based, regulations or knowledge creation system. The foundation of this system consists of a set of rules or regulations designed to operate within a specific context. These rules interact with known facts to deduce new information and make decisions. The knowledge creation process relies on an inference mechanism, particularly deduction, to draw conclusions from established facts. In practical terms, the inference mechanism systematically processes rules, iterating through a list of contexts at each system step. As it traverses the list, it checks whether the prerequisites for a particular rule are satisfied in the current situation. When a rule is found to be applicable, it is executed, contributing to the evolving state of the system. The inference process concludes when either no rules are applicable, or a final fact is confirmed. Navigating a complex environment involves dealing with multiple applicable rules. The outcome of the deduction process may vary depending on the strategy employed whether applying rules one at a time or all simultaneously. However, the fundamental mechanism tends to favor the first encountered option, leading to potential conflicts when multiple rules are in play. Conflict resolution, or control, becomes crucial in determining the direction of the inference mechanism. In the context of a tracking system: 

• The rules are inherently linked to the matrices I^- and I⁺, which are used column-wise. This entails considering the entire set of laws ψ_i along with their traversable rules.

• The initial context is rooted in the original signalization of the tracking system.

• Conflict resolution draws inspiration from concepts in the parallel law Ψ, where the traversal order is randomized, and conflict transitions, which occur when the outcome depends on the order of traversing rules. In cases of ineffective conflict between two laws ψ_i and ψ_j, a decision is made to follow one law while leaving the other unexecuted.

The Tracking System as a Rule System (Grammar)

A tracking system is a unique manifestation of a rule system, distinctly different from general knowledge bases, as it is exclusively constructed based on the concept of node signalizations, representing the values of a complete set of attributes. This notion can be elucidated using constructed words within an alphabet, where the alphabet comprises node identifications such as {v₁, v₂, v₃}. For instance, signalizations, denoted by scenarios like node v1 having three contexts according to law ψ₂ and node v3 with three contexts according to law ψ₄, can be expressed as follows:

Introducing an application ψ, given any signal S, associates a word ψ(S) in v*.v*, where v* represents the set of finite sequences of elements of V, including the empty element ψ. The specific category of rule-based systems corresponding to tracking systems is known as a grammar or a word-rewriting system.

The grammar G=<T,Q> associated with the network Ts=<V,E,δ,Ψ,I^-,I⁺> is defined by:  

• Its terminology T.

• The entire set Q of rewriting rules:

I_s represents the initial signalization S generated by the tracking system, defined as I_s=ψ(S), From this, new words can be formed, establishing a tracking chain. When analyzing traversal sequences, if Ψ is considered an alphabet, Ψ* denotes the complete set of traversal sequences where the order of elements is significant. Conversely, signalizations are elements of V* where the order does not matter.

For instance, take the non-oriented tracking system depicted in figure 5. If we interpret it as a grammar, we have:

The entire set of available signalizations can then be expressed as:

This perspective is crucial as it not only allows for concise notations but, more importantly, establishes a meaningful connection between our tracking system and artificial intelligence techniques. In summary, a tracking system can be comprehensively analyzed from diverse perspectives, each offering unique insights, advantages, and challenges. When considering a moderately-sized graph, it provides an easily interpretable representation that effectively elucidates specific synchronization mechanisms within the system. The multitude of data types associated with each node becomes apparent through signalizations, wherein each type contributes to a dynamic sequence. This sequence subsequently traverses edges corresponding to specific contexts, capturing the nuanced interactions within the system. The material aspect, encapsulated in the fundamental equation, plays a pivotal role by defining a subset of signalizations that must form a traversable sequence. This not only reflects the system’s dynamic behavior but also becomes a critical aspect during the analytical process, guiding our understanding of its underlying structure. Beyond its graphical representation, a tracking system unfolds as a distinctive rule system, a characteristic that assumes paramount importance, especially in the context of broader artificial intelligence techniques with a focus on context-oriented applications. This unique rule-based perspective highlights the system’s adaptability and its potential role in dynamic knowledge representation. In essence, a tracking system, with its multi-faceted nature, emerges as a versatile tool that bridges the gap between specific system dynamics and the broader realm of artificial intelligence methodologies. Its significance lies not only in its immediate applications but also in its potential contributions to advancing context-aware artificial intelligence techniques.

Theoretical modeling and practical case studies in our proposed tracking system

Introduction to Case Example Modeling in Tracking Systems: Bridging Theory and Practice

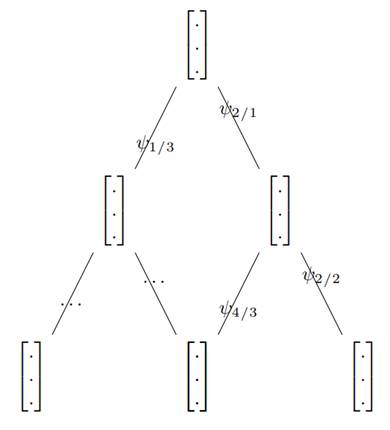
We introduce our theoretical solution for an intelligent tracking system by modeling it on the same principle as automata, which are graph-based computational models or modeling tools. To define our tracking system, we use hypergraphs, mathematical objects that generalize the notion of undirected graphs by allowing edges to connect any number of vertices. This means that the set of vertices in the graph can be divided into several disjoint sets, a partition that encompasses nodes, edges and DTLs depending on the context. Nodes are usually represented graphically by circles, like the states of an automaton, while DTLs are symbolized by triangles. These triangles lie between each separation of two nodes and are responsible for context-sensitive processing of data shared between nodes. Another constraint is that edges (in an undirected graph) only connect nodes to DTLs or DTLs to nodes. There are never any edges directly connecting a node to another node or a DTL to another DTL. Formally, we represent this as figure 1. A tracking system can be modeled in Property 1 succinctly as a triplet consisting of the set of nodes, the set of edges, and the set of incidence functions, DTLs, and the impact matrices I^- and I⁺, often denoted as F for the data flow shared between the nodes. Thus, in the example in figure 6, the set of nodes is (V1,V2,V3) and the set of edges includes four pairs of edges {(e11,e12),(e21,e22),(e31,e32),(e41,e42)}. The flow F is a subset of pairs, either (node,DTL) or (DTL,node). In figure 6, this includes (V₁,ψ₁) and (ψ₁,V₂), etc. It is important to note that the set of nodes and edges is disjoint, as illustrated in figure 6.

Figure 6. Simplified model of a tracking system with nodes, edges, DTLs and data flow

Property 1

A tracking system is an ordered association of six elements belonging to six distinct sets, it is thus a sextuple where:

 T_s=〈V,E,δ,Ψ,I^-,I⁺〉 (structure)Straightforward T_s=〈V,E,F〉.

• V: is a finite or infinite set of nodes, V={v1,v2,…,vn}.

• E: is a finite or infinite set of edges, E={e1,e2,…,en}.

• F: is the set of links, where F⊆(V×E)∪(DTL)∪(E×V) with V∩E=⌀. 

Principle of Signage in Simplified Tracking Systems: Integrating Practical Applications

To define a tracking system based on the principle of hypergraphs, we now need the notion of signaling in property 2. A signaling S of a tracking system is a mapping from the set of nodes to positive integers. Consider an example 7 of a signaling S in a tracking system with three nodes, V₁, V₂, V₃. We can define, for instance, that the number of contextual links is three, the image of ψ₁ is 3, the image of ψ₂ is 1, the image of ψ₃ is 1, and the image of ψ₄ is 2. In our tracking system, the contextual links correspond to the number of signaling elements. ψ₁ equals 3, so we need to establish three links between nodes V₁ and V₂ through the Delta Tracking Law (DTL) ψ₁. ψ₂ equals 1, so there is one contextual link between node V₂ and itself through the Delta Tracking Law (DTL) ψ₂. ψ₃ equals 1, so there is one contextual link between nodes V₂ and V₃ through the Delta Tracking Law (DTL) ψ₃. And so on. Often, instead of describing the signalizations in written form, we represent them as vectors S(3,1,1,2), denoting the signaling of ψ₁, ψ₂, ψ₃, and ψ₄. These characteristics impose an order on the nodes. In V, we arbitrarily order the nodes to establish how many contextual links exist between each node and others. A tracking system is now a quadruple consisting of four elements, the first three form a tracking system graph, and the fourth is the initial signaling of our tracking system. The semantics of our tracking system, therefore, involve evolving the tracking system in property 3 by activating Delta Tracking Laws (DTL) and updating the signalizations. Starting from an initial signaling, we compute different signalizations. This process is non-deterministic, we can potentially activate multiple contextual links via their respective Delta Tracking Laws (DTL), resulting in multiple possible executions. Activating a context or contextual link means data exchange between each preceding node in the Delta Tracking Law (DTL) and the following node, involving all nodes with links through the relevant Delta Tracking Law (DTL). We focus on signaling at least one contextual link in each of these nodes, activate the context in each node, and then activate the context in the nodes posterior to the Delta Tracking Law (DTL), meaning nodes with a link from one to another through a Delta Tracking Law (DTL). For example, in the tracking system with signaling S(3,1,1,2) 8, we can decide to activate the Delta Tracking Law (DTL) ψ₁, considering only contextual links (contexts) 1 and 3. The Delta Tracking Laws (DTL) ψ₂, ψ₃, and ψ₄ are not activatable at this stage for transitioning from signaling S to S’, simply because it’s not needed. Hence, for the transition from signaling S to S’, the only activatable Delta Tracking Law (DTL) is ψ₁. We can activate an infinite number of Delta Tracking Laws (DTL) in a single transition from one signaling to another. Starting with the activation of Delta Tracking Law (DTL) ψ₁, which accounts for contexts 1 and 3 between nodes V₁ and V₂, we discuss a temporary annulment of contextual link 2, transitioning to another state, which is the signaling S’. We can repeat the same process multiple times with any Delta Tracking Law (DTL) in the system. Considering the first two signalizations in 8 as an example, there are three contexts between nodes V₁ and V₂ through Delta Tracking Law (DTL) ψ₁. The transition from signaling S to S’ occurs by activating contexts 1 and 3 of ψ₁, noted as. Thus, we discuss a transition from signaling S to S’ by deactivating the second contextual link. Note that this deactivation is not definitive, we can reactivate this context in other future signalizations.

Property 2

A signage S of a tracking system 〈V,E,F〉 is a mapping from V to N, where each node is associated with an integer.

Informally, S(V) designates the number of contexts in node V.

Thus, a tracking system is a quadruple 〈V,E,F,S₀〉, where 〈V,E,F〉 is a tracking system and S₀ is the initial signage of our tracking system.

Figure 7. Signaling S in a Tracking System with Three Nodes V₁, V₂, V₃

Property 3

Informally, evolving a tracking system means activating (firing) Delta Tracking Laws (DTL) to update the signaling for a DTL : 

· Activating one or more contextual links between a pair of nodes.

· This activation can be performed for the entire system and at different times depending on the system’s behavior.

Figure 8. Signaling S in a Tracking System with Three Nodes V₁, V₂, V₃ with Activation of different Delta Tracking Law’s Context (DTL)

Notions of impact in oriented tracking systems: Integrating Practical Applications

We will now look at important notations in the modeling of a tracking system to calculate or indicate the sets of successors or predecessors of sets of Delta Tracking Laws (DTL), known as the notion of impact. In the tracking system figure 9 and in property 4, V is the set of nodes, E is the set of contextual links or edges, F is the data flow shared between the nodes, and S is the initial signaling. Therefore, for the notations, for any node v, we denote *v as the set of Delta Tracking Laws (DTL) ψ for which there exists an arc going from ψ to v. For example, in figure 9, for v₀, there is no incoming arc to v₀, so  *v₀ is the empty set. For v₁, there are three arcs arriving at v₁, the first comes from ψ₀, the second from ψ₄, and the third from ψ₅, so * v₁ is {ψ₀,ψ₄,ψ₅ }. For any node v, we denote v* as the set of Delta Tracking Laws (DTL) ψ that can be reached from v using an arc from F. From v₁, I can reach ψ₁ with one arc and only ψ₁, so v₁* is {ψ₁ }. Similarly, for v₂*, I can reach ψ₂ and ψ₃, so it is {ψ₂,ψ₃ }. We can define the same concept for Delta Tracking Laws (DTL) ψ, which is completely dual, but this will give sets of nodes. Therefore,  *ψ₀ are the nodes just before ψ₀, in our case 9, it is only v₀. *ψ₁ are the nodes before ψ₁, which is only {v₁ }, and so on. ψ* are the nodes that are after a Delta Tracking Law (DTL). ψ₁* is {v₂ }, ψ₂* is {v₄ }. There is only one arc going from ψ_i to v_i. This extends to sets, where the predecessor set of a node set is the set of Delta Tracking Laws (DTL) ψ that are predecessors of at least one node in the system, and similarly for all other notations. For example, we can calculate figure 9. (*v₃ )*={ψ₃ }*={v₃ }, similarly, (ψ₁* ) =*{v₂ }={ψ₁ } or something more complex like **(v₁*)=**{ψ₁} =*(*{ψ₁ }) =*({v₁ })={ψ₀,ψ₄,ψ₅}. There are the predecessors, the successors of the predecessors of v₃, so first, we calculate the predecessors of v₃, which is just ψ₃, and the successor set of the Delta Tracking Law (DTL) ψ₃ is the node {v₃}. If we calculate this time the last example, which is the set of predecessors of the predecessors of the successors of v₁, it is the set of predecessors of the predecessors of ψ₁, which is the set of predecessors of v₁, so it gives us the set {ψ₀,ψ₄,ψ₅}. These notations are not complicated but are very useful, especially to designate properties and characteristics to certain nodes or certain classes of tracking systems.

Property 4

We assume a tracking system 〈V,E,F,S〉: 

Figure 9. Tracking System Representation of Delta Tracking Laws (DTL) and Contextual Link Impacts in a Tracking System

Consecutive signalling and accessible signalling in tracking systems: Integrating Practical Applications

In this section, we address the concepts of consecutive signaling and accessible signaling in a tracking system figure 10. Two signalizations in a tracking system, S₁ and S₂, are said to be ψ-consecutive for a Delta Tracking Law (DTL) ψ, denoted as. Informally, S₂ is obtained from S₁ by activating the Delta Tracking Law (DTL) like in property 5, which means activating only the first context of the Delta Tracking Law (DTL) ψ₁ while ignoring the second (i.e., ignoring does not mean completely canceling the second context of the Delta Tracking Law (DTL) ψ₁). Formally, for any predecessor node of a DTL ψ, there must be an active context in that link, meaning S₁ (v) must be strictly positive. A contextual link cannot be activated for a signaling transition from S to S’ if there is no history of contextual links between two nodes. Adding one or more contexts between nodes is possible by a complete update of the initial tracking system; this aspect will be addressed in our future work. Now, we distinguish three possible cases. If a node v in a tracking system is preceding but not succeeding ψ, for example, illustrated by the DTL ψ₁ in figure 10, node v₁ precedes ψ₁ figure 10 but does not succeed ψ₁. Therefore, when activating Delta Tracking Law (DTL), we only consider the contexts taken into account by ψ₁ in the transition from S₁ to S₂ and share the data between nodes v₁ and v₃ just through the activated context. This phase of data sharing will also be addressed in the future. Thus, the signaling for this node v will be the signaling minus one. This is the case for node v₃, which follows v₁ but does not precede it. When is activated, v₃ receives the data shared by v₁ that has already been processed by the Delta Tracking Law (DTL) ψ, which we will discuss in our upcoming work. Therefore, the signaling increases externally. For all other nodes, there is no change. For example, node v₄ is not linked to ψ₁ at all, so nothing happens. Or node v₂, which is both before and after ψ₀. The data from v₂ is taken and reinserted into v₂ through ψ₀. Therefore, the signaling on v₂ does not change with the activation of Delta Tracking Law (DTL) ψ₀. For example, if we have the signaling S₁=(2,1,1,1) and activate, we take context 1 for data sharing, and context 2 is temporarily deactivated. This leads to a state where the link between nodes v₁ and v₃ is made only through context 1, resulting in the signaling (1,1,1,1), which verifies its properties figure 10. A signaling in a tracking system is said to be accessible if there exists a sequence of Delta Tracking Laws (DTL) {ψ₀,ψ₁,ψ₂,...,ψ_n} and signalizations {S₀,S₁,S₂,...,S_n} such that we can transition from S₀ to S_n to achieve the desired signaling S by activating a sequence of Delta Tracking Laws (DTL). If it is the initial signaling property 6, for example, in the tracking system 10, we can activate to reach signaling S₂. Then we can activate, etc. Because the activations are non-deterministic, we can reactivate to reach another signaling, reactivate, and continue. In this case, all obtained signalizations can be considered accessible.

Property 5

For a tracking system, two signalizations S₁ and S₂ are said to be ψ-consecutive, where ψ is a Delta Tracking Law (DTL), denoted as:

· For all v∈* ψ, S₁ (v)>0.

· If (v∈* ψ and v∉ψ*) then S₂ (v)=S₁ (v)-1.

· If (v∈ψ*  and v∉* ψ) then S₂ (v)=S₁ (v)+1.

· Else, S₂ (v)=S₁ (v). 

Figure 10. Process of Updating Signaling in a Tracking System Using Delta Tracking Law (DTL)

Property 6

Given a tracking system 〈V,E,F,S₀〉, a signaling S is considered accessible if S=S₀ or if there exist Delta Tracking Laws (DTL) {ψ₁,ψ₂,ψ₃,...,ψ_n } and signalizations {S₁,S₂,S₃,...,S_n } such that:

Accessibility graph for a tracking system: Integrating Practical Applications

Figure 11. Accessibility Graph of a Tracking System with Initial Signaling

In this section, we have discussed the concept of the accessibility graph of a tracking system. Given a tracking system in property 7, a set of nodes, edges, data flow (i.e., the data shared between nodes), and the initial signaling. The accessibility graph is a graph of the set of nodes ∇ and edges Δ, labeled by the Delta Tracking Laws (DTL) of the tracking system. Thus, the set ∇ is the set of all accessible signalizations, meaning the signalizations that can be reached by activating Delta Tracking Laws (DTL) ψ from the initial signaling S₀. Naturally, we place a Delta Tracking Law (DTL) ψ between two accessible signalizations S₁ and S₂ if one can transition from S₁ to S₂ by activating the Delta Tracking Law (DTL) ψ. For example, if we take the tracking system 11 with the initial signaling (1,2,1,1,3), we can calculate its accessibility graph. By activating only, the first and second context in ψ₄, denoted as, we obtain the signaling (1,2,1,1,2). By activating the first context in ψ₁ from the initial signaling, denoted as, we obtain the signaling (1,1,1,1,3). Hence, we see in 11 that we have a finite acyclic graph, but it is possible to obtain any type of graph with tracking systems. In particular, we can have cycles. It is entirely possible to have cyclic graphs in terms of accessibility graphs. It is also possible to obtain an infinite graph. Consider a very simple example figure 12, a simplified tracking system with two nodes v₁ and v₂ and two Delta Tracking Laws (DTL) ψ₁ and ψ₂. We place a single context between v₁ and itself, and then three contexts between v₁ and v₂. We can reactivate the Delta Tracking Law (DTL) ψ₁ and transfer as much contextual information between v₁ and itself as long as the contextual link is unique, making it an infinite loop. Generally, a tracking system is an infinite linking system as long as there is one or more direct contextual links, whereas it becomes a finite linking system by the appearance of indirect contextual links. It should be noted that determining whether the accessibility graph of a tracking system is finite is a decidable property.

Property 7

Given a tracking system 〈V,E,F,S₀〉, we call the accessibility graph of the system the labeled directed graph (Δ,∇), where:  ∇ is the set of accessible signalizations. Δ⊆∇×Ψ×∇, is defined by:

Figure 12. Infinite Loop Example in a Simplified Tracking System with Two Nodes and Two Delta Tracking Laws

Projection of the tracking system in a real-life example: Simple coding and one-way tracking of a traffic light

Figure 13. Modeling of Two Traffic Lights in a Roundabout Using a Tracking System

In this section, we will explore a classic example of modeling two traffic lights using our tracking system. The modeling can be done to track traffic flow in a roundabout. This is a very simplified model, and more complex models with additional nodes and Delta Tracking Laws (DTL) can be created to account for various elements. Figure 13 shows the first light at the top (feu1) and the second light at the bottom (feu2), where light 2 can be modeled with three nodes. One node for the red light, the second node for the green light, and the third for the orange light, with the activation of Delta Tracking Laws (DTL) Ψ* indicating the color of the light. We include a root node v₀ as a central orchestration node for data in our system, with only one contextual link in the system, giving only two possible cases: either the contextual link is activated or not, i.e., zero or one. Therefore, the initial signaling is the activation of one of the Delta Tracking Laws (DTL) ψ₀ or ψ₅ depending on the initial state we want to give the system, and we can evolve our system from there.

Modeling with an orchestrator node is a way to centralize the process. It is extremely common to model with tracking systems everything related to mutual exclusion and resource sharing, with contextual links managing shared resources through the Delta Tracking Law (DTL) for each link to control the shared data. Only one light can be green, and as an example, it is the one activated by the Delta Tracking Law (DTL) Ψ₁*. Initially, the two Delta Tracking Laws (DTL) that can be activated are ψ₀ and ψ₅, both having signaling that allows activation, meaning all predecessor nodes are the root node v₀, which is the orchestrator node. Thus, we can non-deterministically choose to evolve the system, for instance, activating the Delta Tracking Law (DTL) ψ₀ for light1. This results in data sharing between the orchestrator node v₀ and the node v₁ representing the red light in our case, all through ψ₀. We take the data (in this case, light activation) from v₁, and the first light will turn green after data sharing through ψ₁. Then, the only Delta Tracking Law (DTL) that can be activated is ψ₂, and the light will turn orange following the same process. Now, the only activatable Delta Tracking Law (DTL) once again is ψ₅ for light2, and when activated, the light will turn red again, returning to the initial position. The light can then either turn the first light (feu1) to orange or the second light (feu2) to orange, but both lights will never be green at the same time. Only the light with the data can turn green or orange, while the other cannot.

Impact matrix for a tracking system: Integrating Practical Applications

In this section, we focus on the concept of the impact matrix in tracking systems. It is essential to understand what a tracking system is, as illustrated by the micro-example in figure 14, which includes the notion of indirect links and the system being single-context. We define three impact matrices for our tracking system: the impact matrix, denoted as matrix I, and two other impact matrices, the positive impact matrix I⁺ and the negative impact matrix I^-. These matrices have as many columns as the number of Delta Tracking Laws (DTL) and as many rows as the number of nodes. Therefore, to define these matrices, it is necessary to establish an order for the nodes and an order for the Delta Tracking Laws (DTL), which can be arbitrary. This is because the order will produce different matrices up to permutations of the rows and columns, and thus, we choose to number the nodes and the Delta Tracking Laws (DTL). We then distinguish the edges in our tracking system into two classes: those that start from a Delta Tracking Law (DTL) and go to a node, and those that start from nodes and go to the Delta Tracking Laws (DTL). Based on this principle, we define the matrices I⁺ and I^-, from which we will calculate matrix I. This resembles adjacency matrices in graphs. For matrix I^-, each column corresponds to a Delta Tracking Law (DTL). The first column corresponds to Delta Tracking Law (DTL) ψ₁, the second column to ψ₂, and so on. Similarly for the rows, the first row corresponds to node v¹, and so forth. For I^-, we look at the edges going from nodes to the Delta Tracking Laws (DTL) and place either a 1, indicating the existence of a contextual link, or a 0 if not, depending on whether there is an edge going from node i to the corresponding column. For example, in figure 14, there is an edge from v₁ to ψ₁, so we put a 1; an edge from v₁ to ψ₂, so we put a 1; no edge from v₁ to ψ₃, so we put a 0; no edge from v₁ to ψ₄, so we put a 0. Thus, we have the formula for matrix I^-. In a weighted tracking system with multi-context on the edges, we do not use 1s but the number of contexts on each edge. Conversely, for matrix I⁺, we still check for the existence of an edge going from the Delta Tracking Law (DTL) in column j to node i. For instance, for node v₂, if there is an edge from ψ₁ (first column) to v₂ (second row), we place a 1; similarly for an edge from ψ₃ (third column) to v₂ (second row), and so on. This is how we form matrix I⁺. The impact matrix I is then defined as the difference between I⁺ and I^-, as shown in matrix property 8. We can also calculate these directly by examining the inflow and outflow in a directed tracking system. It is interesting to observe what can be inferred from the impact matrix I. Each column corresponds to a Delta Tracking Law (DTL), and the first column, for example, might be (-1, 1, 0, 0), indicating that Delta Tracking Law (DTL) ψ₁ takes data from node v₁, processes it, and shares it with node v₂. Hence, applying Delta Tracking Law (DTL) ψ₁ would transfer data from v₁ to v₂ through ψ₁. Thus, each column represents the data sharing difference in each node when the corresponding Delta Tracking Law (DTL) is activated. These matrices can then be used to establish a link with accessibility. Suppose we start from a signal S and activate Delta Tracking Law (DTL) ψ₁, then ψ₂, then ψ₁, then ψ₂, and finally ψ₃, resulting in a signal S’. This sequence can be depicted as:

All these manipulations can be performed using the impact matrix I by applying a vector to it, without needing to go step by step. That is, we take a row vector like in property 9 which is always of dimension 6, equal to the number of Delta Tracking Laws (DTL) in the system. We count how many times each Delta Tracking Law (DTL) is used in the sequence from S to S’. For instance, ψ₁ is used twice, so the first value is 2, ψ₂ is used twice, so the second value is 2, ψ₃ is used once, so the third value is 1, ψ₄, ψ₅, and ψ₆ are not used, so the fourth, fifth, and sixth values are 0. Multiplying matrix I by the vector (2,2,1,0,0,0) in property 9 results in the vector (-4,2,2,0). This shows that by simply multiplying the matrix in property 9, we can determine the resulting signal. To illustrate the link with accessibility, if we start from an initial signal S₀ and apply Delta Tracking Laws (DTL) ψ₁, ψ₂, ψ₃, ψ₁, ψ₂, etc., we count α₁ as the number of times ψ₁ is used, α₂ for ψ₂, α₃ for ψ₃, and so on. As previously illustrated, the resulting signal is S₀ plus the count of each Delta Tracking Law (DTL) usage, leading to the next signal S₁. Hence, all accessible signals can be written in the form property 10. However, the converse is not always true, meaning that multiplying the impact matrix I by a vector I×α(1,2,3,...,i) may sometimes lead to blockages. For example, Delta Tracking Law (DTL) ψ₃ can only be applied if data is present in node v₂. Therefore, all accessible signals that fit the form property 10 can be used contrapositively, meaning that if a signal does not fit the form property 10, it is not accessible. However, the converse is not necessarily true, as some signals fitting the form property 10 may not be accessible due to certain combinations of Delta Tracking Laws (DTL) being impossible.

Property 8

The impact matrices I⁺, I^-, and I assuming the tracking system in figure 14 is undirected:

And therefore:

For a directed tracking system as shown in figure 14, the impact matrices change, and we have the following new results:

And therefore:

Figure 14. Example of a Directed Tracking System with Indirect Links and Single-Context

Property 9

Property 10

The accessible signalizations are all of the form: 

The converse is generally not true

The notion of node immutability (V- immutable) in a tracking system

The notion of node immutability for a tracking system requires understanding the concept of an incidence matrix of a tracking system, a small example figure 15, if we consider this tracking system with three Delta Tracking Laws (DTL) {ψ₁,ψ₂,ψ₃ } and three nodes {v₁,v₂,v₃}. The Delta Tracking Law (DTL) ψ₁ allows switching data between v₁ and v₂ in three contexts, and ψ₂ dualistically shares data between v₂ and v₃, and finally ψ₃ allows single-context data exchange between v₃ and v₁. What we can notice is that if we take two signals of this tracking system, S and S’ which are consecutive, meaning we move from S to S’ by activating either Delta Tracking Law (DTL) ψ₁, ψ₂, or ψ₃, then the sum of the number of contexts in signal S is the same as the sum of the number of contexts in the following signal S’. For example, if we are in signal S figure 15 with three contexts between v₁ and v₂, two contexts between v₂ and v₃, and only one context between v₃ and v₁, thus a total of six contexts in the system, if we activate Delta Tracking Law (DTL) ψ₁ for contexts 1 and 2, also activate Delta Tracking Law (DTL) ψ₂ for context 1, and finally activate Delta Tracking Law (DTL) ψ₃ for contexts 1, 2, and 3, we removed one context between v₁ and v₂, the same between v₂ and v₃, and added two contexts between v₃ and v₁. We can notice that we still have six contexts, so the total number of contexts in the system is constant, which is an immutable of the tracking system, and we can complicate the notion of immutability in property 11. Now let’s look at another example figure 16 with the first system, it is possible to share data from node v₁ with v₂ via ψ₁, in three possible contexts, it is also possible to share data from node v₁ with v₂ but this time in the first context and through Delta Tracking Law (DTL) ψ₂, we can also notice the possibility of sharing data between v₁ and v₃ in cases, either in two contexts via ψ₃, or in one context via ψ₄. Now let’s look at the number of contexts in our tracking system figure 16, so the number of contexts in the system is the sum of the number of contexts between v₁ and v₂ and between v₁ and v₃ seen as property 11. For example, if we take the initial signal for the two systems figure 16, for the first system we have seven contexts in total in the system. Now if we activate in the first system Delta Tracking Law (DTL) by these two contexts and by the first two contexts, also by these activations, we will get a signal mentioned in the second system figure 16 and property 11, we get a signal where we now have eight contexts in total in the system. We see that this sum of the number of contexts is not constant, and this is where we see the notion of immutability, it is not exactly the sum of contexts between certain nodes that we want to take, but a linear combination of a sum of contexts. If we take this combination figure 16 and property 11 it means we can take twice the number of contexts between v₁ and v₂ mentioned in property 11 by S(v₁,v₂), plus the number of contexts between v₂ and v₁ mentioned in property 11 by S(v₂,v₁), plus the number of contexts between v₁ and v₃ mentioned in property 11 by S(v₁,v₃), plus the number of contexts between v₃ and v₁ mentioned in property 11 by S(v₃,v₁), this equals ten in the signal presented in the third equation in property 11. The same for the second equation, this equals ten in the signal presented in the fourth equation in property 11. What we can notice is that regardless of the Delta Tracking Law (DTL) we activate, whether it is ψ₁, ψ₂, ψ₃, or ψ₄, if we take twice the number of contexts between v₁ and v₂ treated by ψ₁ plus the rest of the number of contexts, we always get a constant. So, we can say that an immutability of a tracking system, that is, whatever Delta Tracking Laws (DTL) we activate, we would always have the same value. More formally as mentioned in property 12. It is the same thing we saw just before in the examples figure 16 and property 11. So, what we want to specify in property 12 is that some α_i can be zero but not all, there is at least one that is not zero, and if we take only zeros, it is obviously something that does not vary in the tracking system but it has no interest. So, it is quite possible that a tracking system has no node immutability, that is, we cannot find a linear combination that satisfies this constraint. We can also notice that if the tuple α₁ to α_k is a node immutability, if we multiply all the α_i by a constant (the same non-zero integer constant), we get a new node immutability. So, from the moment there is necessarily an infinity, a tracking system can have multiple node immutabilities. There is an important link between node immutabilities and the impact matrix of a tracking system which allows us to calculate them all explicitly property 13. We will detail this principle on the first system we had in figure 16 by looking at the third system of this figure which is oriented. We have the impact matrix and we multiply by a vector α_k, we get 0. So, this gives us a linear system property 13, and we can see why the rule in property 13 is valid by looking at the matrix I, it is because each column of the matrix corresponds to a Delta Tracking Law (DTL) and the effect of its activation between each pair of nodes, we can have a vector that preserves a combination, and thus by applying the vector product we get the linear system property 13 that we can solve. We can take as an example of solutions of this system the tuple (α₁,α₂,α₃) such that α₁=α₂=α₃, but we can have other solutions like the tuple (1, 1, 0) which is also a solution. If we take the number of contextual links between v₁ and v₂ plus the number of contextual links between v₂ and v₁ plus the number of contextual links between v₁ and v₃, plus the number of contextual links between v₃ and v₁, it is a constant that does not change with the activation of the contexts in the tracking system. Therefore, the notions of immutability of the tracking system are very useful for observing the cyclic behavior and regularity of the system.

Figure 15. Illustration of Context Conservation in a Delta Tracking System

Property 11

For any signalizations S and S’, and the Delta Tracking Law (DTL) ψ, if S→^ψS’ then:

Figure 16. Example of Context Sharing and Calculation in Different States of a Tracking System

Property 11

We have:

Such as:

Such as:

Property 12

An immutability of a tracking system is an n-tuple (α₁,α₂,...,αk) (of length equal to the number of nodes in the system) of positive integers, not all zero (at least one is ≠0) such that if the signaling S satisfies:

Then for any S’ accessible from S, it satisfies:

• Some α_i can be null, but not all (nonexistence of a link or indirect link)

• A tracking system may have no node immutability.

• ∀λ∈N*, (λα₁,λα₂,...,λα_k) is also a node immutability.

• A tracking system can also have multiple node immutabilities.

Property 13

In a tracking system with impact matrix I, the tuple (α₁,α₂,α₃) of positive integers not all zero is a node immutability if and only if.

Suppose that I is the impact matrix of the third system in figure 16, then:

Therefore, all tuples (α₁,α₂,α₃) such that α₁=α₂=α₃ are node immutabilities.

State Graphs and Link with Finite Automata (Regular Languages)

This section will focus on particular tracking systems called state graphs, with the aim of projecting this notion onto the existence of science. A tracking system is called a state graph if each Delta Tracking Law (DTL) has exactly one incoming arc and one outgoing arc, disregarding the different existing contextual links. This is a property that we read from the Delta Tracking Laws (DTL) of the tracking system. For example, the tracking system in figure 17 is a state graph if we disregard the different contextual links, since the Delta Tracking Law (DTL) ψ₁ has at least one incoming arc from v₁ to v₂, and the same goes for the Delta Tracking Laws (DTL) ψ₂ and ψ₃. Therefore, each Delta Tracking Law (DTL) has at least one incoming and one outgoing arc, making it a state graph. Formally, all tracking systems are state graphs because we cannot have a Delta Tracking Law (DTL) that links more than two nodes. Hence, this is a relatively simple concept.

Figure 17. Illustration of a State Graph in a Tracking System

The main property of tracking systems that are state graphs is that the number of contexts is constant. Since each Delta Tracking Law (DTL) has one outgoing and one incoming arc, when it is executed, it takes the data from one node to share with another node, and this does not change the number of states. There is a strong link with finite automata, meaning that if we take a finite automaton, we can transform it into a tracking system that is a state graph, and this transformation is quite simple. For each Delta Tracking Law (DTL) of the system, which is an arc going from one state to another labeled by a letter, we transform this notion into two arcs plus a Delta Tracking Law (DTL). For example, in figure 18, for the transition labeled a, we take a state in the automaton and the transition a of the automaton will be translated into Delta Tracking Laws (DTL) ψ₁, ψ₄ according to the links of each ψ with the concerned nodes. Similarly, the transition labeled b between states 1 and 2 can be translated into Delta Tracking Law (DTL) ψ₂ between nodes v₁ and v₂. The transition labeled b between states 2 and 0 in the automaton can be transformed in this way to form a tracking system, etc. We can label the Delta Tracking Laws (DTL) when we want to recognize a language by a tracking system, and thus we have a tracking system that recognizes the same thing as an automaton provided, we take the correct signaling. If we take a signaling with a single context and place it in the initial state, then what we can see is that moving this context (sharing data from this context) in this state graph will always keep only one context in the tracking system, because it is a state graph. This corresponds to executing, crossing the transitions of the automaton. As long as we label the Delta Tracking Laws (DTL), we will do exactly the same thing. To have the recognized language, we need to set a final signaling, which is the contextual link in a final state (final node in the system).

Figure 18. Transformation of a Finite Automaton into a State Graph Tracking System

The notion of Coverage in tracking systems: Integrating Practical Applications

We begin our definition of the notion of signaling coverage in a tracking system by taking an example from figure 19. Suppose a leader wants to build a city and brings in a team of engineers who tell him the construction process of a city, which starts with the existence of a village as the base. Stones and materials are needed to build the city, and wheat to feed the workers, for example. There is an entire process to track the construction. To complicate the process a bit, we imagine a large tracking system with the objective of tracking the construction cycle of the city. The fundamental questions they might ask concern accessibility. For example, they need to know if, starting from the initial signaling figure 19, which consists of eight stones, six wheat, and one village, and no data in the intermediate nodes of our tracking system illustrated in the example, nor any data in the city, which will be the last node (the final state of the process). We can build this city without any resource loss, meaning there are no resources left unused (a problem with the system’s data). This is interesting for the project manager to ensure a correct and fair process where all resources taken are used to build the city. This is the notion of accessibility, which means that from one signaling, we can reach another specific signaling. This notion is difficult on an algorithmic level. A fundamental question that arises is whether, taking the same example figure19, we can actually build the city with the eight stone resources, the six wheat resources, and the village, regardless of any leftover data circulating in the system that remains in the factory? This means, is it true that we can build the city no matter the rest? These questions are not the same but are much easier to resolve on an algorithmic level. Formally speaking property 14, in a tracking system, a signaling S covers a signaling S’ or is greater than the signaling S’, noted as an order relation, if for every node, the number of contextual links in S is greater than or equal to the number of contextual links in S’. For example, if we have a small tracking system figure 20 with different signallings, the first (2,4,6) and the second (4,8,6), the signaling S covers the signaling S’. So, the question we can ask is whether, starting from an initial signaling S, we can reach a signaling S’? To answer this question, we can apply the KAP-MILLER algorithm to our tracking system to find an accessible signaling S that covers S’.

Property 14

In a tracking system, a signaling S covers a signaling S’, denoted S’⩽S, if for every node V: 

Figure 19. Illustration of an Example of Resource Accessibility and Coverage in a Tracking System

Figure 20. Example of Signaling Coverage in a Tracking System

Omega-signals in tracking systems (ω-signals)

In this section, we are interested in the notion of omega-signaling in tracking systems. This concept is based on the principle of signaling in tracking systems and is used to solve coverage problems, particularly in the KAP-MILLER algorithm. An omega-signaling in a tracking system figure 21 and property 15, is a basic signaling, except that we can assign an infinite number of contexts between nodes, which we denote with the symbol ω. Formally, it is a mapping that associates each pair of nodes with a number of contexts, either an integer or ω, which is infinite. So why omega ω and not the infinity symbol? This is because we are dealing more with ordinals than cardinals, and ω is the symbol of the first ordinal, Omega. This concept should be seen as an infinite number of contexts between nodes. For example, in the tracking system figure 21, we can take a signaling between nodes v₁ and v₂ and associate it with ω, meaning an infinity of contexts between node v₁ and v₂, two contexts between node v₁ and v₃, a single context between v₃ and itself, and finally an infinity of contexts between node v₂ and v₃, also associated with ω. We can then extend all classical notions of tracking systems to Omega-signaling, such as the activation of Delta Tracking Law (DTL). If we start from this signaling (ω,ω,1,2) and wish to activate the second context of Delta Tracking Law (DTL) ψ₄, this means. If we want to deactivate contexts {3,7,12} of Delta Tracking Law (DTL) ψ₁, this means , then the data sharing between node v₁ and v₃ will only be done by the second contextual link, and the data sharing between node v₁ and v₂ will be done by all contextual links except contexts 3, 7, and 12. However, since there is an infinite number of contextual links, adding or removing one or more contexts still leaves an infinite number of contexts. The notion of coverage naturally extends to the notions of Omega-signaling as well, meaning that an Omega-signaling S₁ is greater than or covers an Omega-signaling S₂ if all components of S₁ are greater than or equal to the components of S₂, with the convention that Omega is greater than or equal to any integer. For example, (4,ω,6,6)⩾(3,3,6,3) is a classic coverage with only integers, where 4 is greater than or equal to 3, ω is greater than or equal to 3, 6 is greater than or equal to 6, and 6 is greater than or equal to 3. Therefore, the first signaling, which is greater, covers the second signaling, which is an Omega-signaling (ω-signaling).

Property 15

An ω-Signaling of a tracking system graph (V,E,F) is a mapping from V to N∪{ω}. ω contexts are as infinite as we want, as shown in figure 21.

Figure 21. Example of Omega-Signaling and Context Activation in a Tracking System

Understanding the KAP-MILLER algorithm and projecting it onto the coverage problem in tracking systems

This section will be dedicated to the coverage problem in tracking systems and the utility of the Karp-Miller algorithm in this context. Karp-Miller is a generic algorithm for partially ordered and applied systems. In this section, we will explore the notions of signaling, coverage, ω-signaling, etc., which were explained previously. Let us begin by modeling the problem as follows: we have a tracking system and we are given a signaling S₁. The fundamental question is whether we can activate the tracking system from the initial signaling to reach a signaling S₂ that covers S₁, meaning that the number of contextual links between each pair of nodes in S₂ is greater than or equal to the number of contextual links between each pair of nodes in S₁, which means S₂⩾S₁.

Figure 22. Illustration of the Karp-Miller Tree for Coverage in a Tracking System

The calculation of all accessible signaling of our tracking system and comparing them each time to see if one is greater than the other from S₁. But the accessibility graph of a tracking system can be infinite, so the algorithm will not work. The Karp-Miller algorithm will try to look at a certain number of repetitions to answer this question.

There are several ways to present the Karp-Miller algorithm. There are variants, ways to cut, reductions, etc. In this section, we will outline the general idea applied to our tracking system. For our future studies, they will be done differently and in a more in-depth manner, applied in other ways. We will draw our tracking system, imagining that our system signals as shown in figure. 22, and by activating the Delta Tracking Laws (DTL), we will obtain the final signaling figure 22. There are 4 nodes in the system and we have applied Delta Tracking Laws (DTL). The idea is to look at when we have a chain figure 22 and to see each time we add an element. So, we start from the first signaling, we have activated the Delta Tracking Laws (DTL) and we obtain the second signaling. Does it strictly cover a previous signaling? That is, there is at least one pair of nodes where there is a strictly greater number of contexts. So, the first signaling does not cover the second. We continue this way for each signaling n with signaling n-1. The idea is that we cannot have an infinite sequence of signaling without at some point having a signaling that is greater than another. This is what happens in the last signaling in figure 22, we have (4,3,1,3), this signaling strictly covers the first signaling. There is an equality of contextual links in the first and second pairs of nodes, but there are strictly more contextual links in the last two pairs of nodes. It also strictly covers the penultimate signaling. So, when we start in our tracking system, four contextual links in the first Delta Tracking Law (DTL), three in the second, none in the third, and two in the fourth, we can apply Delta Tracking Law (DTL) activations and reach the last signaling. If we repeat the activation of infinite contexts of Delta Tracking Laws (DTL) ψ₁, ψ₂, ψ₃, ψ₄, from the new last signaling, we can restart several times and have as many contextual links as we want between all pairs of nodes in the system. We can then replace the signaling values with ω and thus obtain the following signaling (ω,ω,ω,ω).

Figure 23. Sequence of Signaling Activations Leading to Coverage in a Tracking System

So, the idea of the Karp-Miller algorithm in this context is to construct, from the initial signaling, a covering tree of the accessibility graph. Each time we detect the phenomenon described before, i.e., adding a signaling, we compare it with those preceding it in the tree, and if it is greater than or equal (i.e., there is at least one pair of nodes where there is a strictly greater number of contextual links in terms of integers, not an infinite number, but an integer number), then we replace by ω the Delta Tracking Laws (DTL) where it is strictly greater in terms of integers. This will always yield a final tree. Let’s take this small example. We have a tracking system figure 23 with the possibility of a single contextual link at most between the pairs of nodes (v₁,v₂), (v₂,v₃), and v₂ and itself, and an infinity of contextual links between node v₁ and v₃. So, the initial signaling is (1,0,0,1). We start by considering the absence of contextual links for Delta Tracking Laws (DTL) ψ₂ and ψ₃, meaning the existence of an indirect link. We will activate the single contextual link for Delta Tracking Laws (DTL) and three contexts for, and we will move to the signaling (1,3,1,1) which covers the first signaling. We can continue in this way until we find a tree from the accessibility graph of the system. For example, we can go from the signaling (1, 3, 1, 1) to the infinite contextual links for Delta Tracking Law (DTL) ψ₂, and arrive at the signaling (1,ω,1,1) and continue this way. It is possible to construct a tree, not a covering tree in the proper sense of the accessibility graph because we have ω-signaling, but if a signaling S₂ is coverable by a tracking system, it is coverable by one of the elements of the accessibility graph. Just compare with all the elements of the graph and we will have our coverage problem solved. 

• So, a signaling S is coverable, meaning there exists an accessible signaling that covers it if in the Karp-Miller tree example, there is an ω-signaling that covers it.

• What we can demonstrate is that the Karp-Miller algorithm always terminates. That is, we cannot have an infinite sequence of incomparable ω-signaling, meaning there is always a point in the tree where we will place ω and then at some point, we will stop

• There are many optimization variants.

• Depending on the order in which we process, the order in which we make comparisons, whether we do a breadth-first search, depth-first search, etc., the way we construct the covering tree will yield a different Karp-Miller tree.

Conflict-free tracking system

We will now discuss the concept of conflict-free tracking systems. This notion is simply defined as a tracking system in which each node has at most one outgoing edge figure 24 or outgoing arc in the case of a directed tracking system figure 25.

Figure 24. Conflict-Free Tracking System Example

Indeed, the operation of a tracking system involves activating Delta Tracking Laws (DTLs) to share data according to a specific context. If a node has two outgoing edges, there are two DTLs that might want to use the data in this node, causing a conflict between the two DTLs. This conflict manifests in the nodes. For example, the directed tracking system figure 26 is not conflict-free because node v₁ has two outgoing arcs, as does node v₂. This means that if we have data in v₁, we might want to use it either with ψ₁ or ψ₃.

Figure 25. Directed Conflict-Free Tracking System with Single Outgoing Arcs

If we decide to remove the link between node v₁ and the DTL ψ₃ and also remove the link between node v₂ and the DTL ψ₅, we can then examine node by node what happens figure 27. Node v₁ has only one outgoing arc. Node v₂ has only one outgoing arc towards ψ₂. Node v₃ has no outgoing arcs. Node v₄ has only one outgoing arc towards ψ₄. And node v₅ has no outgoing arcs. So, each node has either zero or one outgoing arc. This is, therefore, a conflict-free network.

Figure 26. Directed Tracking System with Conflicting Outgoing Arcs

In this case, the system becomes a distributed system, and there is a risk of data loss between every pair of nodes, which is entirely contradictory to the purpose of our tracking system.

Figure 27. Conflict-Free Tracking System with Single Outgoing Edges

Tracking system with contextual weighting

Tracking systems with weighted edges, also known as tracking systems with contextual weights. To recap, in a tracking system figure 6, when we want to activate a Delta Tracking Law (DTL) ψ₁ for example, we initiate a contextual data sharing between node v₁ and v₂, meaning there is an edge that goes from node v₁ to v₂ or vice versa through the Delta Tracking Law (DTL) ψ₁. The same process is valid for the entire system, which is how simple tracking systems operate. Tracking systems with weighted contextual links or with contextual weights figure 28, add a power to each contextual link representing the context weight, which is a strictly positive integer. Sometimes we refer to multi-contexts because there are no weights, but we say that, for example, from ψ₁ to v₂ figure 28 there are not just one edge but three. The operation of a tracking system with contextual weights is entirely similar; when we want to activate a Delta Tracking Law (DTL), for example, instead of sharing data between nodes v₁ and v₂ according to the second context in general, we distribute this data to sub-contexts that constitute the parent context, and the number of sub-contexts is represented by a power in the context number.

Thus, we can read figure 28 as follows: 

• There are three contextual links between node v₁ and v₂ that pass-through Delta Tracking Law (DTL) ψ₁, the first context has no sub-context, but the second context has two sub-contexts, and the third context has seven sub-contexts.

• There is a single contextual link between node v₂ and itself that passes through Delta Tracking Law (DTL) ψ₂, this context has three sub-contexts.

• There are two contextual links between node v₂ and v₃ that pass-through Delta Tracking Law (DTL) ψ₃, the first context has three sub-contexts, but the second context has no sub-context.

• There is a single contextual link between node v₃ and v₁ that passes through Delta Tracking Law (DTL) ψ₄, this context has two sub-contexts.

We can define all notions similarly, such as signaling, consecutive signaling, signaling graph, etc. They can simulate one another. Sometimes having weighted edges is a bit more compact for expressing the use of multiple resources at once without having to duplicate nodes or Delta Tracking Laws (DTL).

Figure 28. Weighted Contextual Links in a Tracking System

Bounded tracking system, Safe tracking system

This section will address the notions of bounded tracking systems as well as safe tracking systems. Firstly, we need to understand the concepts of our tracking system defined in the previous sections of this article, such as signaling and the accessibility graph, etc. The notion of ω-signalling might also be useful but is not entirely necessary. Let us consider a positive integer d. A tracking system is d-bounded if there can never be more than d contexts between a pair of nodes. More formally in property 17, a tracking system is d-bounded if for any accessible signalling S and any nodes (v_i,v_j), S(v_i,v_j)⩽d, meaning the number of contextual links between nodes v_i and v_j is less than or equal to d. We mention the tracking system in figure 29 as 3-bounded. Consider the tracking system figure 29, with an initial signaling of (2,3,2,1,1,1). We can construct its accessibility graph presented in property 16, and we can see that throughout the entire accessibility graph, there are never more than three contextual links activated between the nodes of the system, making it a 3-bounded system. We can derive the following conclusions:   

• A tracking system is said to be bounded if there exists an integer d such that it is d-bounded. 

• A tracking system is bounded if and only if its accessibility graph is finite. Indeed, if it is bounded, it is d-bounded for a given integer, and the number of possible accessible signalings is maximized. This means all possible signalling values are at most d to the power of the number of nodes, which is finite, hence the accessibility graph is finite. Conversely, if the accessibility graph is finite, we just need to look at the signalling in which the nodes have the highest number of contexts between them, and it will be d-bounded.

Equivalently, a tracking system is bounded if and only if there is no accessible -signalling. This provides, using the Karp-Miller algorithm, a much more efficient way to determine if a tracking system is bounded.

Now, a tracking system is said to be safe if it is -bounded, meaning there is at most one contextual link between the nodes of the system.

Property 16

Property 17

Let d be a positive integer. A tracking system is d-bounded if for any accessible signalling S, and any node v, S(v)⩽d. 

• A tracking system is bounded if there exists a d such that it is d-bounded.

• A tracking system is bounded if and only if its accessibility graph is finite.

• A tracking system is bounded if and only if there is no accessible ω-signalling.

Figure 29. An Example of a d-Bounded Tracking System, specifically 3-Bounded

Advantages of tracking systems

A tracking system rooted in graph theory and hypergraph theory offers a multitude of advantages, enhancing its applicability across diverse domains. These benefits include:

Clear Representation of Relationships: graphs and hypergraphs serve as powerful tools for portraying intricate relationships between elements in a visually intuitive manner. This clarity aids in data visualization, making it easier to discern patterns and identify underlying models.

Effective Data Manipulation: hypergraphs, with their ability to model complex data structures, provide a robust framework for representing information that might pose challenges for traditional graphs. This capability facilitates the efficient processing of large and intricate datasets.

Identification of Groups and Communities: the inherent structure of graphs and hypergraphs allows for the identification of groups and communities among interconnected elements. This feature is particularly beneficial for applications such as social network analysis, fraud detection, and the identification of clusters sharing common attributes.

Real-time Tracking of Data Changes: the dynamic nature of graphs and hypergraphs enables real-time updates to reflect changes in the underlying data. This real-time tracking capability is invaluable for promptly detecting significant alterations and understanding the evolving nature of the data.

Adaptability to Different Data Types: graphs and hypergraphs exhibit remarkable versatility in representing diverse data types, including both structured and unstructured data. This adaptability ensures a comprehensive approach to data analysis, allowing for a nuanced representation of relationships spanning various elements.

CONCLUSIONS

In conclusion, this paper introduces a sophisticated tracking system designed for objects and living beings, capitalizing on the robust principles of both graphs and hypergraphs. By formulating a multi-context linking system, our tracking theory offers a versatile and comprehensive approach that surpasses existing methods, particularly those confined to conventional graphs. Hypergraph-based techniques, as demonstrated in our framework, exhibit broader applicability and a more nuanced understanding of complex relationships. The proposed method encompasses two essential aspects. Firstly, it incorporates a theoretical foundation rooted in hypergraphs, which naturally extends to encompass graphs as a specific case. This segment is tailored for tracking objects and living beings in diverse contexts. It introduces a tracking law that governs the intricacies of data sharing within the system and the subsequent processing of this shared data through specific functions. To validate its practical efficacy, experiments can be conducted with real-world datasets, offering insights into the system’s performance relative to other existing methods. On the other front, our contribution to the field of tracking goes beyond mere amalgamation by introducing a novel tracking law. This law facilitates sophisticated interactions between elements within a system, introducing a layer of adaptability and complexity not previously explored in existing works. Unlike conventional approaches, our formulation eliminates the need for prior knowledge regarding the number of tracking targets, rendering our system dynamic and capable of evolving as situations unfold. Looking ahead, future research efforts should focus on several key areas. Enhancements to the system’s performance can be achieved by developing general functions that operate on generic parameters, ensuring broader applicability and efficiency. Furthermore, refining the theoretical underpinnings by introducing additional rules and expanding the system’s adaptability will contribute to its resilience across diverse scenarios.

BIBLIOGRAPHIC REFERENCES

1. Hallinan, Maureen T.” Tracking: From theory to practice.” Sociol- ogy of education 67.2 (1994): 79-84.

2. S. Pellegrini, A. Ess, and L. Van Gool. Improving data association by joint modeling of pedestrian trajectories and groupings. In Eu- ropean Conference on Computer Vision, pages 452–465. Springer, 2010.

3. S. Pellegrini, A. Ess, and L. Van Gool. Improving data association by joint modeling of pedestrian trajectories and groupings. In Eu- ropean Conference on Computer Vision, pages 452–465. Springer, 2010.

4. W. Hu, T. Tan, L. Wang, S. Maybank, A survey on visual surveil- lance of object motion and behaviors, IEEE Trans. Syst. Man Cy- bern., Part C, Appl. Rev. 34 (3) (2004) 334–352.

5. Bretto, Alain.” Hypergraph theory.” An introduction. Mathemati- cal Engineering. Cham: Springer (2013).

6. Dawei Du, Honggang Qi, Longyin Wen, Qi Tian, Qingming Huang, and Siwei Lyu. 2017. Geometric hypergraph learning for visual tracking. IEEE TC 47, 12 (2017), 4182–4195.

7. Tutte, William Thomas, and William Thomas Tutte. Graph theory. Vol. 21. Cambridge university press, 2001.

8. West, Douglas Brent. Introduction to graph theory. Vol. 2. Upper Saddle River: Prentice hall, 2001.

9. Gould, Ronald. Graph theory. Courier Corporation, 2012.

10. Bollob´as, B´ela. Modern graph theory. Vol. 184. Springer Science & Business Media, 1998.

11. Bondy, John Adrian, and Uppaluri Siva Ramachandra Murty. Graph theory with applications. Vol. 290. London: Macmillan, 1976.

12. Bretto, Alain.” Hypergraph theory.” An introduction. Mathemati- cal Engineering. Cham: Springer (2013).

13. Hopkins, Brian, and Robin J. Wilson.” The truth about K¨onigsberg.”  The College Mathematics Journal 35.3 (2004):  198- 207.

14. Hallinan, Maureen T.” Tracking: From theory to practice.” Sociol- ogy of education 67.2 (1994): 79-84.

15. H. B. Shitrit, J. Berclaz, F. Fleuret, and P. Fua, “Multi-commodity network flow for tracking multiple people,” IEEE TPAMI, vol. 36, no. 8, pp. 1614–1627, 2014.

16. D. Reid et al., “An algorithm for tracking multiple targets,” IEEE transactions on Automatic Control, vol. 24, no. 6, pp. 843–854, 1979.

17. G. Shu, A. Dehghan, O. Oreifej, E. Hand, and M. Shah, “Part- based multiple-person tracking with partial occlusion handling,” in Proc. CVPR. IEEE, 2012, pp. 1815–1821.

18. Y. Tian, A. Dehghan, and M. Shah, “On detection, data association and segmentation for multi-target tracking,” IEEE Transactions on Pattern Analysis and Machine Intelligence, pp. 1–1, 2018.

19. Idir Filali, Mohand Sa¨ıd Allili, and Nadjia Benblidia. 2016. Multi- scale salient object detection using graph ranking and global–local saliency refinement. Elsevier Signal Proc. Image 47 (2016), 380–401.

20. Meng Li and Howard Leung. 2016. Multiview skeletal interaction recognition using active joint interaction graph. IEEE TM 18, 11 (2016), 2293–2302.

21. H. K. Meena, K. K. Sharma, and S. D. Joshi. 2017. Improved facial expression recognition using graph sig. pro. IET EL 53, 11 (2017), 718–720.

22. Dawei Du, Honggang Qi, Wenbo Li, Longyin Wen, Qingming Huang, and Siwei Lyu. 2016. Online deformable object tracking based on structure-aware hyper-graph. TIP 25, 8 (2016), 3572–3584.

23. H. Nam, M. Baek, and B. Han. 2016. Modeling and propagating CNNs in a tree structure for visual tracking. CoRR. Retrieved from abs/1608.07242.

24. Tao Wang and Haibin Ling. 2018. Gracker: A graph-based planar object tracker. IEEE TPAMI 40, 6 (2018), 1494–1501.

25. D. Yeo, J. Son, B. Han, and J. H. Han. 2017. Superpixel-based tracking-by-segmentation using Markov chains. In Proceedings of the CVPR. IEEE, 511–520.

26. K. Okuma, A. Taleghani, N. De Freitas, J. J. Little, and D. G. Lowe. A boosted particle filter: Multitarget detection and tracking. In Computer Vision-ECCV 2004, pages 28–39. Springer, 2004.

27. C. Huang, B. Wu, and R. Nevatia. Robust object tracking by hierarchical association of detection responses. In Computer Vi- sion–ECCV 2008, pages 788–801. Springer, 2008.

28. Y. Xiang, A. Alahi, and S.  Savarese.  Learning to track:  On- line multi-object tracking by decision making. In Proceedings of the IEEE International Conference on Computer Vision, pages 4705–4713, 2015.

29. M. D. Breitenstein, F. Reichlin, B. Leibe, E. Koller-Meier, and L. Van Gool. Robust tracking-by-detection using a detector confidence particle filter. In Computer Vision, 2009 IEEE 12th International Conference on, pages 1515–1522. IEEE, 2009.

30. A. Robicquet, A. Sadeghian, A. Alahi, and S. Savarese. Learning so- cial etiquette: Human trajectory understanding in crowded scenes. In European Conference on Computer Vision, pages 549–565. Springer, 2016.

31. A. Alahi, K. Goel, V. Ramanathan, A. Robicquet, L. Fei-Fei, and S. Savarese. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 961–971, 2016.

32. S. Pellegrini, A. Ess, K. Schindler, and L. Van Gool. You’ll never walk alone: Modeling social behavior for multi-target tracking. In Computer Vision, 2009 IEEE 12th International Conference on, pages 261–268. IEEE, 2009.

33. K. Yamaguchi, A. C. Berg, L. E. Ortiz, and T. L. Berg. Who  are you with and where are you going? In Computer Vision and Pattern Recognition (CVPR), 2011 IEEE Conference on, pages 1345–1352. IEEE, 2011.

34. W. Choi and S. Savarese. Multiple target tracking in world co- ordinate with single, minimally calibrated camera. In Computer Vision–ECCV 2010, pages 553–567. Springer, 2010.

35. P. Scovanner and M. F. Tappen. Learning pedestrian dynamics from the real world. In Computer Vision, 2009 IEEE 12th Inter- national Conference on, pages 381–388. IEEE, 2009.

36. S. Ali and M. Shah. Floor fields for tracking in high density crowd scenes. In Computer Vision–ECCV 2008, pages 1–14. Springer, 2008.

37. Z. Wu, A. Thangali, S. Sclaroff, and M. Betke. Coupling detection and data association for multiple object tracking. In Computer Vi- sion and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 1948–1955. IEEE, 2012.

38. S. Oron, A. Bar-Hillel, and S. Avidan. Real-time trackingwith-detection for coping with viewpoint change. Machine Vision and Applications, 26(4):507–518, 2015.

39. S. Tang, B. Andres, M. Andriluka, and B. Schiele. Multiperson tracking by multicut and deep matching. In European Conference on Computer Vision, pages 100–111. Springer, 2016.

40. N. Le, A. Heili, and J.-M. Odobez. Long-term time-sensitive costs for crf-based tracking by detection. In European Conference on Computer Vision, pages 43–51. Springer, 2016.

41. H. Izadinia, V. Ramakrishna, K. M. Kitani, and D. Huber. Multi-pose multi-target tracking for activity understanding. In Applica- tions of Computer Vision (WACV), 2013 IEEE Workshop on, pages 385–390. IEEE, 2013.

42. A. R. Zamir, A. Dehghan, and M. Shah. Gmcp-tracker: Global multi-object tracking using generalized minimum clique graphs. In Computer Vision–ECCV 2012, pages 343– 356. Springer, 2012.

43. B. Y. S. Khanloo, F. Stefanus, M. Ranjbar, Z.-N. Li, N. Saunier, T. Sayed, and G. Mori. A large margin framework for single cam- era offline tracking with hybrid cues. Computer Vision and Image Understanding, 116(6):676– 689, 2012.

44. S. Hong and B. Han. Visual tracking by sampling treestructured graphical models. In European Conference on Computer Vision, pages 1–16. Springer, 2014.

45. H. Nam and B. Han. Learning multi-domain convolutional neural networks for visual tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 4293–4302, 2016.

46. D. Held, S. Thrun, and S. Savarese. Learning to track at 100 fps with deep regression networks. In European Conference on Com- puter Vision, pages 749–765. Springer, 2016.

47. L. Leal-Taixe, C. Canton-Ferrer, and K. Schindler. Learning ´ by tracking: Siamese cnn for robust target association. arXiv preprint arXiv:1604.07866, 2016.

48. M. Zhai, M.  J.  Roshtkhari, and G.  Mori.  Deep learning of appearance models for online object tracking. arXiv preprint arXiv:1607.02568, 2016.

49. B. Yang and R. Nevatia. Multi-target tracking by online learning of non-linear motion patterns and robust appearance models. In Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 1918–1925. IEEE, 2012.

50. B. Yang and R. Nevatia. An online learned crf model for multi-target tracking. In Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on, pages 2034–2041. IEEE, 2012.

51. C. Dicle, O. I. Camps, and M. Sznaier. The way they move: Tracking multiple targets with similar appearance. In Proceedings of the IEEE International Conference on Computer Vision, pages 2304–2311, 2013.

52. D. Helbing and P. Molnar. Social force model for pedestrian dy- namics. Physical review E, 51(5):4282, 1995.

53. Mgalaa, S., Mabrouki, J., Elouardi, M., El Azzouzi, L., Moufti, A., El Hajjaji, S., ... & El Belghiti, M. A.. Study and evaluation of the degradation of procion blue dye by the ozonation method: parametric and isothermal study. Nanotechnology for Environmental Engineering, 7(3), 691-697. 2022.

54. L. Wen, Z. Lei, S. Lyu, S. Z. Li, and M.-H. Yang. Exploiting hier-archical dense structures on hypergraphs for multi-object tracking. IEEE transactions on pattern analysis and machine intelligence, 38(10):1983–1996, 2016.

55. B. Zhan, D. N. Monekosso, P. Remagnino, S. A. Velastin, and L.-Q. Xu. Crowd analysis: a survey. Machine Vision and Applications, 19(5-6):345–357, 2008.

56. F. Solera, S. Calderara, E. Ristani, C. Tomasi, and R. Cucchiara. Tracking social groups within and across cameras. IEEE Transac- tions on Circuits and Systems for Video Technology.

57. X. Zhao, D. Gong, and G. Medioni. Tracking using motion patterns for very crowded scenes. In Computer Vision–ECCV 2012, pages 315–328. Springer, 2012.

58. P. Mordohai and G. Medioni. Dimensionality estimation, manifold learning and function approximation using tensor voting. Journal of Machine Learning Research, 11(Jan):411–450, 2010.

59. L. Kratz and K. Nishino. Tracking with local spatio-temporal motion patterns in extremely crowded scenes. In Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on, pages 693–700. IEEE, 2010.

60. L. Kratz and K.  Nishino.  Tracking pedestrians using local spatio-temporal motion patterns in extremely crowded scenes. IEEE transactions on pattern analysis and machine intelligence, 34(5):987–1002, 2012.

61. M. Rodriguez, S. Ali, and T. Kanade. Tracking in unstructured crowded scenes. In 2009 IEEE 12th International Conference on Computer Vision, pages 1389–1396. IEEE, 2009.

62. El Alouani, M., Aouan, B., Rachdi, Y., Alehyen, S., El Herradi, E. H., Saufi, H., ... & Barka, N. Porous geopolymers as innovative adsorbents for the removal of organic and inorganic hazardous substances: a mini-review. International Journal of Environmental Analytical Chemistry, 1-13. 2022.

63. X. Wang, Intelligent multi-camera video surveillance: a review, Pattern Recognit. Lett. 34 (1) (2013) 3–19.

64. J. Candamo, M. Shreve, D.B.  Goldgof, D.B.  Sapper, R.  Kas- turi, Understanding transit scenes: a survey on human behavior- recognition algorithms, IEEE Trans. Intell. Transp. Syst. 11 (1) (2010) 206–224.

65. Benchrifa, M., Elouardi, M., Fattah, G., Mabrouki, J., & Tadili, R. Identification, simulation and modeling of the main power losses of a photovoltaic installation and use of the internet of things to minimize system losses. In Advanced technology for smart environment and energy, 49-60. 2023.

66. I.S. Kim, H.S. Choi, K.M. Yi, J.Y. Choi, S.G. Kong, Intelligent visual surveillance-a survey, Int. J. Control. Autom. Syst. 8 (5) (2010) 926–939.

67. D.A. Forsyth, O. Arikan, L. Ikemoto, J. O’Brien, D. Ramanan, et al., Computational studies of human motion: part 1, tracking and motion synthesis, Found. Trends Comput. Graph. Vis. 1 (2–3) (2006) 77–254.

68. A. Yilmaz, O. Javed, M. Shah, Object tracking: a survey, ACM Comput. Surv. 38 (4) (2006) 13.

69. X. Li, W. Hu, C. Shen, Z. Zhang, A. Dick, A.V.D. Hengel, A survey of appearance models in visual object tracking, ACM Trans. Intell. Syst. Technol. 4 (4) (2013) 58.

70. Mabrouki, J., Azrour, M., Dhiba, D., Farhaoui, Y., & El Hajjaji, S. IoT-based data logger for weather monitoring using arduino-based wireless sensor networks with remote graphical application and alerts. Big Data Mining and Analytics, 4(1), 25-32. 2021.

71. L. Leal-Taix´e, A. Milan, I. Reid, S. Roth, K. Schindler, MOTChal- lenge 2015: towards a benchmark for multi-target tracking, arXiv:1504.01942, http://arxiv.org/abs/1504.01942. 

72. Azrour, M., Mabrouki, J., Guezzaz, A., & Farhaoui, Y. New enhanced authentication protocol for internet of things. Big Data Min Analytics 4 (1): 1–9. 2020.

73. L. Wen, D. Du, S.  Li, X.  Bian, and S.  Lyu, “Learning nonuniform hypergraph for multi object tracking,” arXiv preprint arXiv:1812.03621, 2018.

74. H. Sheng, Y. Zhang, J. Chen, Z. Xiong, and J. Zhang, “Hetero- geneous association graph fusion for target association in multiple object tracking,” IEEE Transactions on Circuits and Systems for Video Technology, 2018.

75. S. Ren, K. He, R. Girshick, and J.  Sun, “Faster R-CNN:  To- wards Real-Time Object Detection with Region Proposal Net- works,” IEEE TPAMI, vol. 39, no. 6, pp. 1137–1149, 2017.

76. Azrour, M., Mabrouki, J., Fattah, G., Guezzaz, A., & Aziz, F. Machine learning algorithms for efficient water quality prediction. Modeling Earth Systems and Environment, 8(2), 2793-2801, 2022.

77. J. Redmon and A. Farhadi, “YOLO9000: Better, Faster, Stronger,” 2016.

78. Mabrouki, J., Azrour, M., Fattah, G., Dhiba, D., & El Hajjaji, S. Intelligent monitoring system for biogas detection based on the Internet of Things: Mohammedia, Morocco city landfill case. Big Data Mining and Analytics, 4(1), 10-17, 2021.

79. K. Shafique and M. Shah, “A noniterative greedy algorithm for multiframe point correspondence,” IEEE transactions on pattern analysis and machine intelligence, vol. 27, no. 1, pp. 51–65, 2005.

80. Mabrouki, J., Bencheikh, I., Azoulay, K., Es-Soufy, M., & El Hajjaji, S. Smart monitoring system for the long-term control of aerobic leachate treatment: dumping case Mohammedia (Morocco). In Big Data and Networks Technologies 3 (pp. 220-230). Springer International Publishing, 2020.

81. G. Shu, A. Dehghan, O. Oreifej, E. Hand, and M. Shah, “Part- based multiple-person tracking with partial occlusion handling,” in Proc. CVPR. IEEE, 2012, pp. 1815–1821.

82. A. Roshan Zamir, A. Dehghan, and M. Shah, “GMCP-tracker: Global multi-object tracking using generalized minimum clique graphs,” in Lecture Notes in Computer Science, 2012.

83. B. Wu and R. Nevatia, “Detection and tracking of multiple, par- tially occluded humans by bayesian combination of edgelet based part detectors,” International Journal of Computer Vision, vol. 75, no. 2, pp. 247–266, 2007.

84. A. Dehghan, S. Modiri Assari, and M. Shah, “Gmmcp tracker: Globally optimal generalized maximum multi clique problem for multiple object tracking,” in Proc. CVPR, 2015, pp. 4091 4099.

85. H. Pirsiavash, D. Ramanan, and C. C. Fowlkes, “Globally-optimal greedy algorithms for tracking a variable number of objects,” Proc. CVPR, pp. 1201–1208, 2011.

86. A. A. Butt and R. T. Collins, “Multi-target tracking by lagrangian relaxation to min-cost network flow,” in Proc. CVPR, 2013, pp. 1846–1853.

87. J. Berclaz, F. Fleuret, E. Turetken, and P. Fua, “Multiple ob- ¨ ject tracking using k shortest paths optimization,” IEEE TPAMI, vol. 33, no. 9, pp. 1806–1819, 2011.

88. H. B. Shitrit, J. Berclaz, F. Fleuret, and P. Fua, “Multi-commodity network flow for tracking multiple people,” IEEE TPAMI, vol. 36, no. 8, pp. 1614–1627, 2014.

89. B. Leibe, K. Schindler, N. Cornelis, and L. Van Gool. Coupled ob- ject detection and tracking from static cameras and moving vehi- cles. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 30(10):1683–1698, 2008.

90. A. Milan, S. Roth, and K. Schindler. Continuous energy minimiza- tion for multitarget tracking. IEEE transactions on pattern analysis and machine intelligence, 36(1):58–72, 2014.

91. K. Shafique, M. W. Lee, and N. Haering. A rank constrained con- tinuous formulation of multi-frame multi-target tracking problem. In Computer Vision and Pattern Recognition, 2008. CVPR 2008. IEEE Conference on, pages 1–8. IEEE, 2008.

92. Q. Yu, G. Medioni, and I. Cohen. Multiple target tracking using spatio-temporal markov chain monte carlo data association. In 2007 IEEE Conference on Computer Vision and Pattern Recognition, pages 1–8. IEEE, 2007.

93. S. Oron, A. Bar-Hille, and S. Avidan. Extended lucaskanade track- ing. In European Conference on Computer Vision, pages 142–156. Springer, 2014.

94. Yilmaz, Alper, Omar Javed, and Mubarak Shah.” Object tracking: A survey.” Acm computing surveys (CSUR) 38.4 (2006): 13-es.

95. McKenna, Stephen J., et al.” Tracking groups of people.” Computer vision and image understanding 80.1 (2000): 42-56.

96. Zhou, Xingyi, Vladlen Koltun, and Philipp Kr¨ahenbu¨hl.” Tracking objects as points.” Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part IV. Cham: Springer International Publishing, 2020.

97. Ariss A, Ennejjai I, Mabrouki J, Lamjid A, Kharmoum N, Ziti S. Tracking System for Living Beings and Objects: Integration of Accessible Mathematical Contributions and Graph Theory in Tracking System Design. Data and Metadata. 2024 Aug 16;3:376-.

98. Pirela CV, Plata AO, Hernandez GL. Strategic thinking as a potential factor in the growth of companies in the dairy sector. Management (Montevideo) 2024;2:40–40. https://doi.org/10.62486/agma202440.

99. Sonal D, Mishra K, Haque A, Uddin F. A Practical Approach to Increase Crop Production Using Wireless Sensor Technology. LatIA 2024;2:10–10. https://doi.org/10.62486/latia202410.

100. Vargas OLT, Agredo IAR. Active packaging technology: cassava starch/orange essential oil for antimicrobial food packaging. Multidisciplinar (Montevideo) 2024;2:102–102. https://doi.org/10.62486/agmu2024102.

101. Velazquez MDCR, Chririnos AAN, Brito AV. Decision-making styles developed by commercial enterprises in the municipality of Barrancas. Management (Montevideo) 2024;2:35–35. https://doi.org/10.62486/agma202435.

102. Ariss A, Ennejjai I, Kharmoum N, Rhalem W, Ziti S, Ezziyyani M. Tracking Methods: Comprehensive Vision and Multiple Approaches. InInternational Conference on Advanced Intelligent Systems for Sustainable Development 2022 May 22 (pp. 40-54). Cham: Springer Nature Switzerland.

FINANCING

No financing.

CONFLICT OF INTEREST

None.

AUTHORSHIP CONTRIBUTION

Conceptualization: Anass Ariss.

Data curation: Anass Ariss, Imane Ennejjai, Jamal Mabrouki, Soumia Ziti.

Formal analysis: Anass Ariss.

Research: Anass Ariss, Imane Ennejjai, Jamal Mabrouki, Soumia Ziti.

Methodology: Anass Ariss, Imane Ennejjai, Jamal Mabrouki, Soumia Ziti.

Supervision: Anass Ariss, Soumia Ziti.

Validation: Anass Ariss, Soumia Ziti.

Drafting - original draft: Anass Ariss, Imane Ennejjai.

Writing - proofreading and editing: Anass Ariss, Imane Ennejjai.