doi: 10.56294/dm2024.423

ORIGINAL

Agent technology to detect failures in continuous processes

Tecnología de agentes para detectar fallos en procesos continuos

Carlos Arturo Parra Ortega¹ *, Javier Mauricio García Mogollón² *, Jarol Darley Ramón Valencia¹ *

¹Universidad de Pamplona, Facultad de Ingenierías y Arquitectura. Pamplona, Colombia.

²Universidad de Pamplona, Facultad de Ciencias Económicas y Empresariales. Pamplona, Colombia.

Citar como: Parra Ortega CA, García Mogollón JM, García Mogollón JD. Tecnología de agentes para detectar fallos en procesos continuos. Data and Metadata 2024; 3:.423. https://doi.org/10.56294/dm2024.423

Enviado: 27-02-2024                   Revisado: 01-06-2024                   Aceptado: 10-09-2024                 Publicado: 11-09-2024

Editor: Adrian Alejandro Vitón Castillo

Autor para la correspondencia: Carlos Arturo Parra Ortega *

ABSTRACT

Introduction: to control a continuous production system whose components are exposed to failures, it is necessary to provide intelligence to the monitoring mechanism, due to the need to identify the type of failure, its source, and anticipate the consequences that arise from its occurrence.

Method: in this paper, it is proposed to extend Sanz’s multi-resolution model and apply it to a supervision scheme with event detection based on fuzzy logic and implemented using agent technology.

Results: a mechanism to validate the implementation using discrete event simulation is also presented.

Conclusions: it was concluded that discrete event simulation constitutes an appropriate way to validate a supervisory control system at a high level.

Keywords: Agents; Discrete-Event Systems; Failure Detection; Reasoning Schemes.

RESUMEN

Introducción: para controlar un sistema de producción continua cuyos componentes están expuestos a fallas, es necesario dotar de inteligencia al mecanismo de monitoreo, debido a la necesidad de identificar el tipo de falla, su origen y anticipar las consecuencias que se derivan de su ocurrencia.

Método: en este trabajo se propone extender el modelo multiresolución de Sanz y aplicarlo a un esquema de supervisión con detección de eventos basado en lógica difusa e implementado mediante tecnología de agentes.

Resultados: también se presenta un mecanismo para validar la implementación mediante simulación de eventos discretos.

Conclusiones: se concluyó que la simulación de eventos discretos constituye una vía adecuada para la validación de sistema de control supervisorio a un alto nivel.

Palabras clave: Agentes; Sistemas Discretos; Detección de Fallos; Esquemas de Razonamiento.

INTRODUCCIÓN

El control automatizado de procesos industriales continuos es una labor crítica, debido a que existen procesos que se pueden detener mientras se presentan diversas situaciones que afectan la configuración, como cambios en las especificaciones del producto o en el flujo de materia prima.⁽¹⁾ Entre las pocas situaciones que justifican detener un proceso se encuentran los fallos causados por el mal funcionamiento de diversos dispositivos. Sin embargo, un fallo detectado a tiempo a veces no hace necesaria la detención de un proceso industrial, y el costo de su reparación es menor que el costo de lo dejado de producir debido a la parada de planta.⁽²⁾

Los fallos son uno de los eventos con los que frecuentemente se cuenta dentro del control de un proceso. Generalmente pueden deberse a un daño o malfuncionamiento del equipamiento, errores en la medición de variables, insumos deficientes o a una combinación de estos factores.⁽³⁾

 Generalmente, los Sistemas de Control Supervisorio (SCS de aquí en adelante) están diseñados para controlar a un alto nivel aquellos procesos en condiciones normales. El objetivo en este documento es el de presentar una propuesta de usar tecnología de agentes para supervisar un sistema de producción continua con eventos de fallos ocasionales, de manera que no se haga necesario detener el proceso, y además se pueda diagnosticar el tipo de falla para proponer una medida que permita resolver en tiempo real, dentro de las posibilidades del sistema, una condición de fallo es generada mediante simulación.

Para lograr la especificación anteriormente mencionada, se integran las metodologías de síntesis de SCS usando autómatas, Lógica Difusa para detectar eventos y condiciones de fallo, modelo de razonamiento multiresolucional para obtener leyes de control a partir de condiciones de operación observadas, y sistemas multi-agente basados en lógica para implementar los supervisores y detectores de eventos en un entorno distribuido.⁽⁴⁾ El diseño resultante se valida por medio de modelado y simulación de sistemas a eventos discretos, aplicados a un sistema de control de agua y presión como caso de estudio.

 Algunos trabajos se han desarrollado en estas áreas: Cerrada et al.⁽⁵⁾ proponen un diseño basado en agentes para la detección de fallas en procesos industriales, con roles específicos para cada tipo de agente, y basado en especificación general (reglas puntuales). Guillén et al.⁽⁶⁾ proponen métodos para detectar fallas utilizando transformada wavelet en procesos químicos; Altamiranda et al.⁽⁷⁾ utilizan el modelo multiresolucional para detectar fallas en procesos de refinación de crudo, utilizando lógica difusa en el mecanismo de detección de eventos. Parra Ortega et al.⁽⁸⁾ proponen una arquitectura del sistema de soporte a la toma de decisiones en control, extendiendo el modelo multiresolucional de Sanz junto con técnicas basadas en lógica difusa. Barboza et al.⁽⁹⁾ diseñan esquemas de supervisión inteligente, al igual que mecanismos de ajustes de los mismos propuestos por Kim et al.⁽¹⁰⁾. Una proyección de los mecanismos de supervisión a los gemelos digitales también fue desarrollada por Jiang et al.⁽¹¹⁾. Este documento está organizado así: primero se presenta el problema que origina este trabajo, luego se establece una propuesta sobre cómo integrar supervisión y tecnología de agentes, luego se pasa a un caso de estudio; el mecanismo de validación se describe en la sección cinco, mientras que en la sección seis se muestran los resultados experimentales obtenidos. Posteriormente se presentan las conclusiones derivadas de la realización de este trabajo.

Control distribuido de procesos continuos

El control automático de procesos industriales continuos es una labor crítica, debido a que un proceso no se puede detener así cambien las condiciones de operación. Una de las condiciones ideales del control de procesos es obtener la máxima disponibilidad, es decir, de un valor cercano al cien por ciento de los recursos de operación operando en el tiempo.⁽¹²⁾ Desafortunadamente, los eventos de fallo están siempre presentes, bien sea debido a un malfuncionamiento o daño del equipamiento industrial, perturbaciones en el proceso de medición de variables, interpretación errónea del estado en que se encuentra un proceso, procedimientos inadecuados ejecutados sobre los insumos, o a una combinación entre algunos de los factores ya mencionados. En los procesos continuos esta situación es crítica, ya que implica detener el proceso para llevar a cabo las acciones correctivas necesarias y luego re-arrancar el mismo, con las consiguientes pérdidas en tiempo y económicas.⁽¹³⁾

En tales procesos continuos es necesario medir las variables pertenecientes al proceso que se está controlando para detectar la ocurrencia de eventos. Algunas veces estas mediciones están sujetas a perturbaciones que pueden originarse en la naturaleza de las variables a medir, como por ejemplo la ocurrencia de oleaje en depósitos sujetos a flujo de entrada y salida, ingreso de material adicional no previsto (lluvias en depósitos) o en la calibración de los dispositivos de medición, por citar algunos casos. Dado que en los sistemas de producción las variables de estado del proceso son de naturaleza discreta, hay una función de proyección de variables continuas a estados discretos (p. ej: bajo, alto, medio, normal, fallo). Para sistemas con las características de perturbación mencionadas anteriormente no pueden utilizarse reglas puntuales para deducir cambios en la región de operación, ya que puede ocurrir que durante un período de tiempo se conmute sucesivamente de una región a otra, de acuerdo al período de muestreo de los dispositivos de medición, ocasionando que se tomen medidas de control antes de estabilizarse el sistema, o por oscilaciones pequeñas que no implican un cambio de estado, lo cual no es recomendable en misiones de control críticas. Además, algunos elementos que pertenecen al sistema de producción también pueden presentar fallas, que de alguna manera se van a reflejar en las variables medidas y cuya ocurrencia es difícil de detectar de manera directa.

Una forma de solucionar el problema de supervisar procesos continuos con fallos de diversa índole consiste en integrar los SCS basados en autómatas, como lo proponen Cassandras y Lafortune ⁽¹⁴⁾; aplicar técnicas de control inteligente extendiendo el modelo multiresolucional de Sanz⁽⁴⁾ para generar decisiones a partir de variables del comportamiento dinámico de un proceso; los modelos de IA basados en lógica difusa para tratar con datos sujetos a grandes perturbaciones o con tendencias cambiantes; y la tecnología de agentes inteligentes para implementar en un entorno distribuido como lo es una planta industrial, y se gana en facilidades de comunicación y colaboración.^(15,16,17)

Diseño del modelo de razonamiento

La extensión al modelo multiresolucional de Sanz se puede apreciar en la figura 1, donde el punto de partida es un modelo numérico aplicado a los principios físicos y mediciones de variables de interés sobre las condiciones de operación de los procesos (modelo N), un modelo cualitativo local (modelo CL) para describir la lógica de las operaciones, un modelo cualitativo global (modelo CG) que describe el estado general del proceso, y un modelo de razonamiento (modelo R) para representar el conocimiento en forma de reglas lógicas que se implementen en software. La toma de decisiones en un SCS se fundamenta en el uso de modelos apropiados capaces de describir el comportamiento dinámico del proceso a controlar. Mediante tales modelos es posible determinar acciones de control frente a la ocurrencia de perturbaciones aleatorias o cambios en las condiciones de operación, que garantizan su estabilidad y confiabilidad operacional.

Esta representación de comportamiento tiene como resultado la generación de planes de acuerdo a un propósito inicial que lleve a metas intermedias y a partir de estas, llegar a acciones puntuales. Sin embargo, esta representación prevé cambios repentinos mediante el apareamiento de observaciones de condición-acción para activar una acción o cambiar un plan. Este modelo de razonamiento se muestra en la figura 1. Como puede apreciarse, se basa en combinar varios modelos produciendo un razonamiento flexible para que los agentes lleven a cabo sus metas de control en un entorno cambiante.

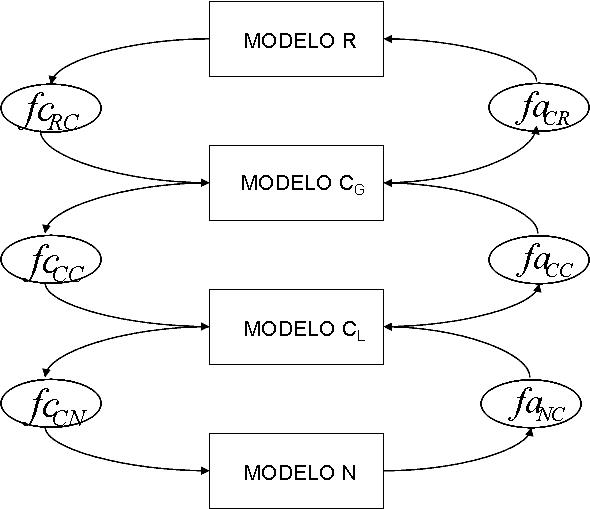
Figura 1. Modelo multiresolucional extendido

Estos modelos multiresolucionales en ambientes de supervisión y contropermiten:

· Describir comportamientos dinámicos de los procesos ante perturbaciones o acciones de control.

· Proporcionar información pertinente y actualizada sobre el estado de los procesos.

· Facilitar la comunicación entre procesos y usuarios.

Esos modelos se acoplan conceptualmente por medio de funciones de abstracción y funciones de concreción para especificar valores de variables de un nivel a partir de valores de variables en otros niveles. El esquema de acople se puede apreciar en la figura 2, donde el comportamiento del Proceso Físico que está situado en el piso de planta se describe por un modelo numérico que aplica principios físicos como conservación de masa y energía, así como la disponibilidad de mediciones de variables de interés sobre las condiciones de operación de los procesos. Estos procesos presentan perturbaciones físicas, de manera que los datos que miden las variables son muestreados y llevados al Detector de Eventos, el cual a partir de los valores medidos y el estado actual del proceso aplica una función de abstracción que proyecta estos valores hacia eventos, que recibe el Supervisor, el cual tiene los modelos cualitativos y racional de todo el proceso. Estos eventos que recibe modifican un Modelo Cualitativo Local, que contiene las condiciones de operación ideales o normales. Algunos de estos eventos detectados sugerirán eventos de orden global con la función Fa_CC, lo que sugiere la ocurrencia de eventos que indican posibles fallos. El modelo racional contiene la imagen del proceso, denominada en otros conceptos como el gemelo digital, la cual proyecta, desde un autómata global y otro local, hacia unas reglas que los agentes traducen en acciones enviadas a dispositivos de control. Los eventos controlables se planifican de acuerdo a las reglas que contiene el modelo R.

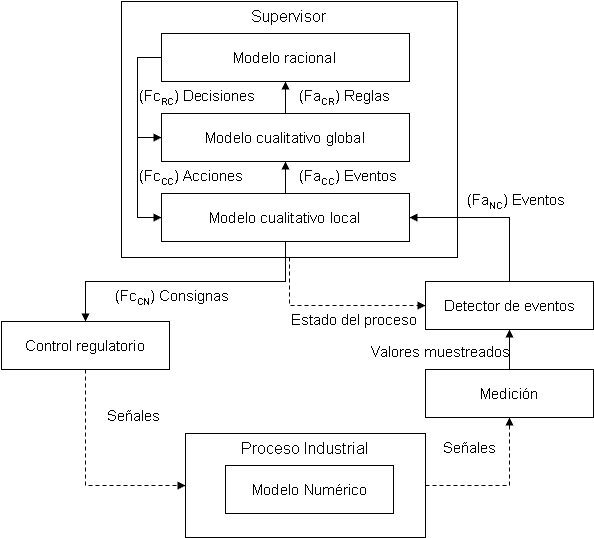
Figura 2. Esquema que combina el modelo multiresolucional con control supervisorio

A partir del modelo racional se aplican unas funciones de concreción en forma de actualización de los estados tanto del modelo cualitativo global (cuando se recupera una falla), como del modelo cualitativo local (operación en condiciones normales). A partir del modelo local se generan las reglas Fc_CN del control regulatorio hacia el proceso físico, que permite que el controlador provoque cambios en las propiedades físicas del proceso, afectando al modelo numérico, reiniciando el ciclo con medición y detección de eventos.

Software de Agentes

Dentro del contexto de informática, el término “Agente” se asocia a la IA distribuida, donde se crean instancias de diversas aplicaciones en una red, las cuales cooperan para lograr una meta. No existe una definición única de agente, ya que el contexto de aplicación varía desde lo muy general a lo particular. La definición más general es la de Russell y Norvig⁽¹⁸⁾, que establece que agente es “toda entidad que observa su ambiente, razona sobre lo observado, y actúa en función de unas metas”; hasta una definición muy instrumental, como la de Kowalski⁽¹⁹⁾, que establece que un agente es “una pieza de software para controlar un dispositivo capaz de interactuar con su entorno, percibiendo y produciendo cambios en ese entorno”. Con las anteriores definiciones, podría establecerse que las personas, robots, softbots, dispositivos e inclusive un termostato se consideran agentes. Para efectos de este documento, se consideró al agente como un software con características especiales.

Por extensión, un sistema multi-agente (SMA de aquí en adelante) sería un conjunto de agentes, los cuales comparten el mismo entorno, y actúan coordinadamente para lograr un conjunto de metas. Una vez especificado el comportamiento de un agente o un grupo de agentes, la implementación en un entorno computacional es un aspecto crítico. Por cierto, los más utilizados se basan en el lenguaje Java, debido a que permite cierto nivel de introspección en los agentes, cuyo proceso de razonamiento los lleva a decidir cuáles de sus métodos utilizar en medio de un ciclo de razonamiento. Implementaciones se han llevado a cabo como, por ejemplo, el trabajo de Hernández Cruz et al.⁽²⁰⁾, relacionados con monitoreo de procesos.

Actualmente se han construido plataformas integradas de desarrollo, las cuales facilitan la implementación de los sistemas multi-agente. Entre estas, vale la pena mencionar a JADE, ZEUS, INGENIAS y AnyLogic. Se seleccionó a JADE debido a que implementa una clase especial para agentes, con comportamientos cíclicos temporizados y un protocolo de comunicación basado en FIPA-OS, lo que libera al desarrollador de tener que programar toda la comunicación entre agentes. Solo debe preocuparse del contenido de los mensajes. Una ventaja de este entorno es que se basa en el lenguaje Java, lo que lo hace compatible con otras clases que implementen los mecanismos de razonamiento de los agentes.

Implementación computacional

Se aplicó el SMA para gestionar la imagen del proceso como si fuera el gemelo digital del proceso continuo real. Uno de los agentes implementa al detector de eventos para recibir las lecturas de sensores que miden el proceso físico, donde existen dispositivos con probabilidad de fallar. Con la tendencia de los datos medidos, el agente detector aplica un conjunto de reglas difusas para determinar cuál región de operación es la actual, a partir de los datos, o si ocurrió un cambio en la región. También puede detectar fallos a partir de un análisis de los datos. Otro agente implementa al Supervisor con sus reglas de razonamiento cargadas para tener la capacidad de conmutación y flexibilidad si cambian las condiciones del sistema. Estas reglas están especificadas en Lógica de Primer Orden, según el modelo de Kowalski. Las premisas de las reglas condición-acción corresponden a la evolución del autómata, como las de los modelos Cualitativos local y global. Otras reglas que no están relacionadas con el autómata corresponden a la comunicación entre agentes. La figura 3 ilustra la forma en que se implementa el SCS con los agentes supervisor y detector de eventos.

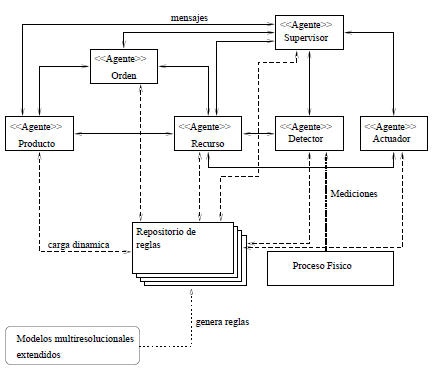
Figura 3. Esquema de implementación con agentes de un SCS

CASO DE ESTUDIO

Como caso para probar el SCS en un sistema continuo con fallos, se tiene en control un sistema hidroneumático residencial en un edificio. El sistema a supervisar tiene los siguientes componentes: un depósito cilíndrico de agua en forma horizontal, que contiene agua y aire, alimentado por un depósito externo, una motobomba y un compresor. El objetivo global del sistema consiste en suministrar agua a los residentes, manteniendo los niveles de su depósito y presión de aire dentro del rango de valores adecuado. La presión del aire determina la calidad de suministro para la demanda de agua de los residentes, por lo tanto, también se debe controlar. Si el nivel de agua desciende más allá del tope mínimo, se debe ingresar agua por medio de una motobomba, mientras que, si sube más allá del tope máximo, se detiene el bombeo. La medición del nivel del agua tiene oleajes, de manera que se trata de una medición perturbada. Por otra parte, el compresor, la motobomba y los sensores de nivel y presión pueden presentar fallos en cualquier momento, que se traducen en resultados que no corresponden de acuerdo al comportamiento esperado del sistema, como lo establece el SCS. Los valores donde debe oscilar el nivel del depósito están entre 0,65 y 1,22 m, mientras que la presión del sistema debe oscilar entre 1,43 y 5,17 kg-f/cm2. El esquema de este sistema lo podemos apreciar en la figura 4:

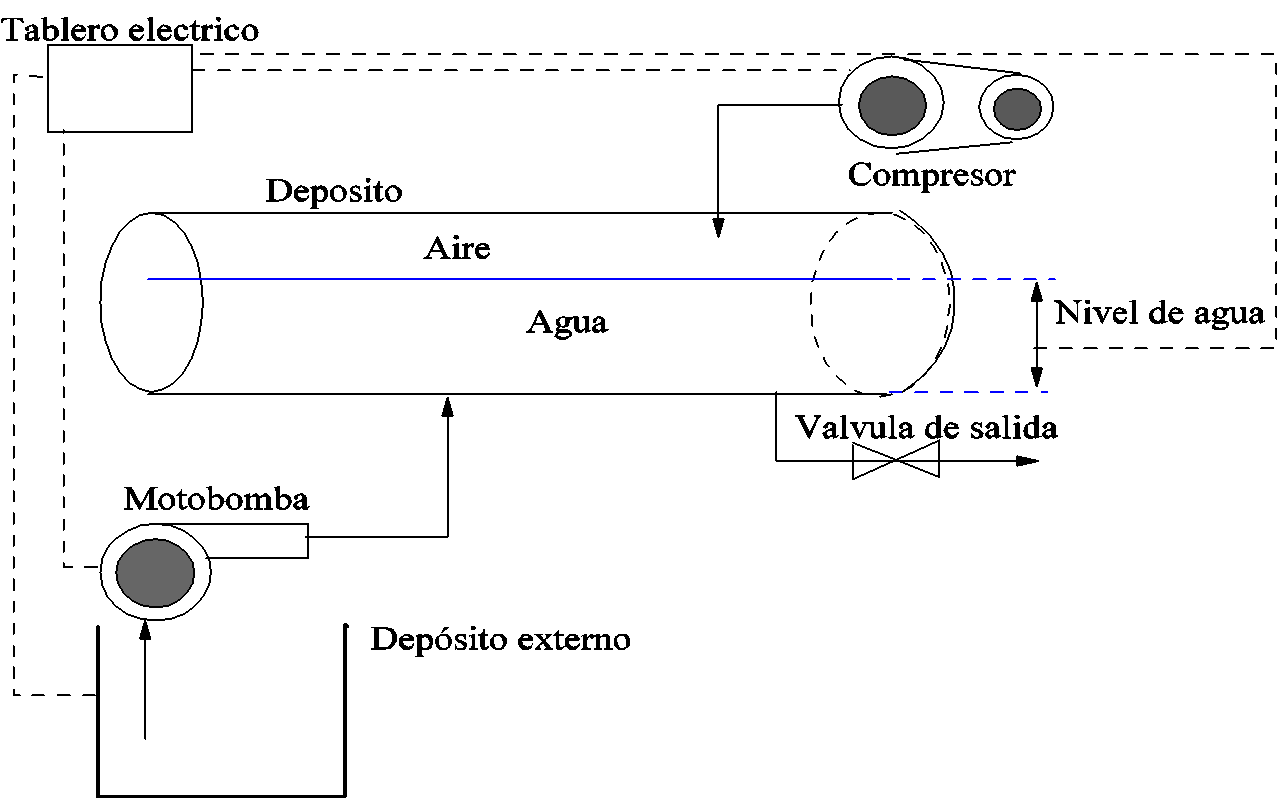
Figura 4. Esquema sistema hidroneumático

Modelo numérico

Para describir el comportamiento físico del sistema se considerará como variables de estado el nivel de agua y la presión en el tanque cilíndrico horizontal. Estas variables se representaron usando ecuaciones diferenciales ordinarias.

El nivel del depósito se expresó mediante la siguiente ecuación:

        (1)

Donde h'(t) es la tasa de cambio del nivel de agua en el tanque y h es la altura instantánea, en un instante determinado. La presión se da por la expresión.

       (2)

P1 es la presión en un instante t, P0 es la presión en el instante t=0, V1 y V0 son los volúmenes ocupados por el agua en los instantes t y t=0, respectivamente.

Modelo cualitativo local

Este modelo describe los estados discretos en operación normal. Para describir el comportamiento físico del sistema se consideraron como variables de estado el nivel de agua y la presión en el depósito, y tres cualificaciones discretas: alto, medio y bajo que resultan de sus valores tope. Por consiguiente, se obtuvieron nueve regiones de operación, como se pueden apreciar en la figura 5.

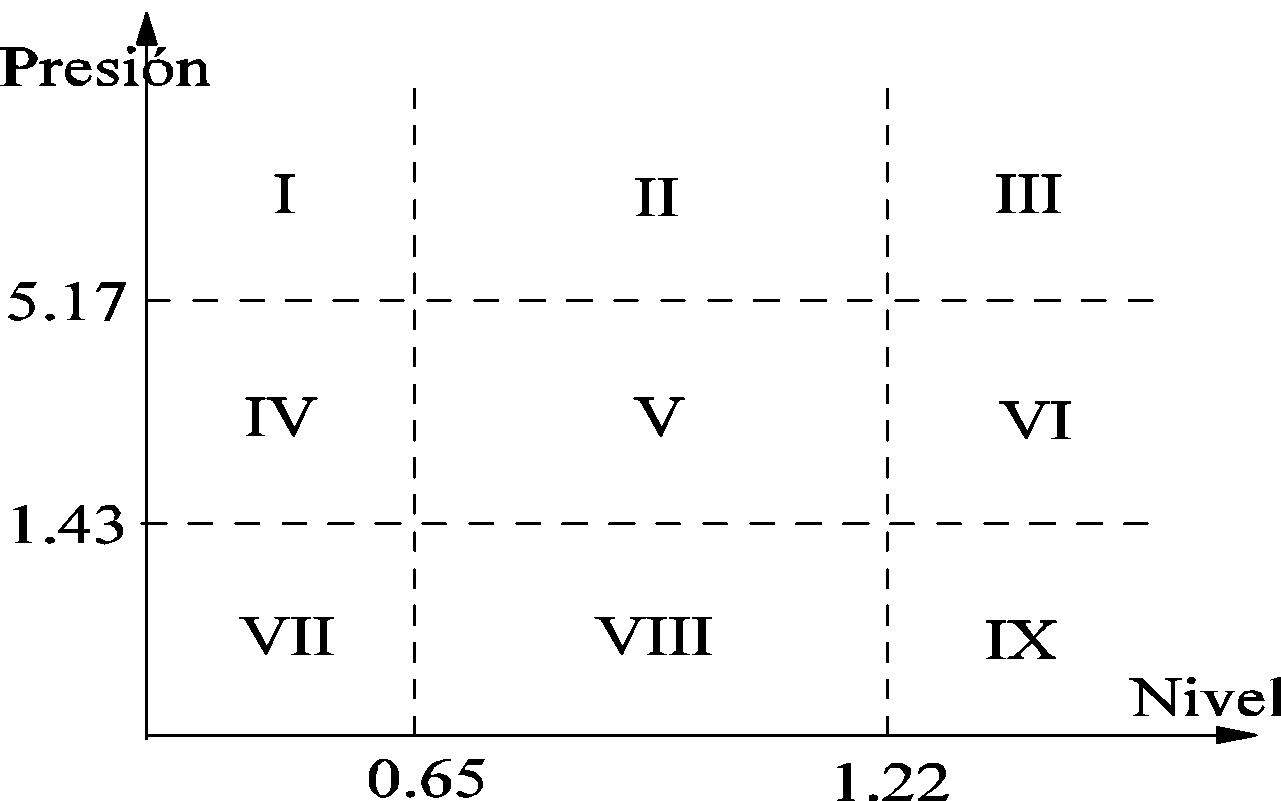
Figura 5. Regiones de operación en condiciones normales

Estas regiones de operación se pueden proyectar a un autómata de estados finitos, como el que muestra la figura 6.

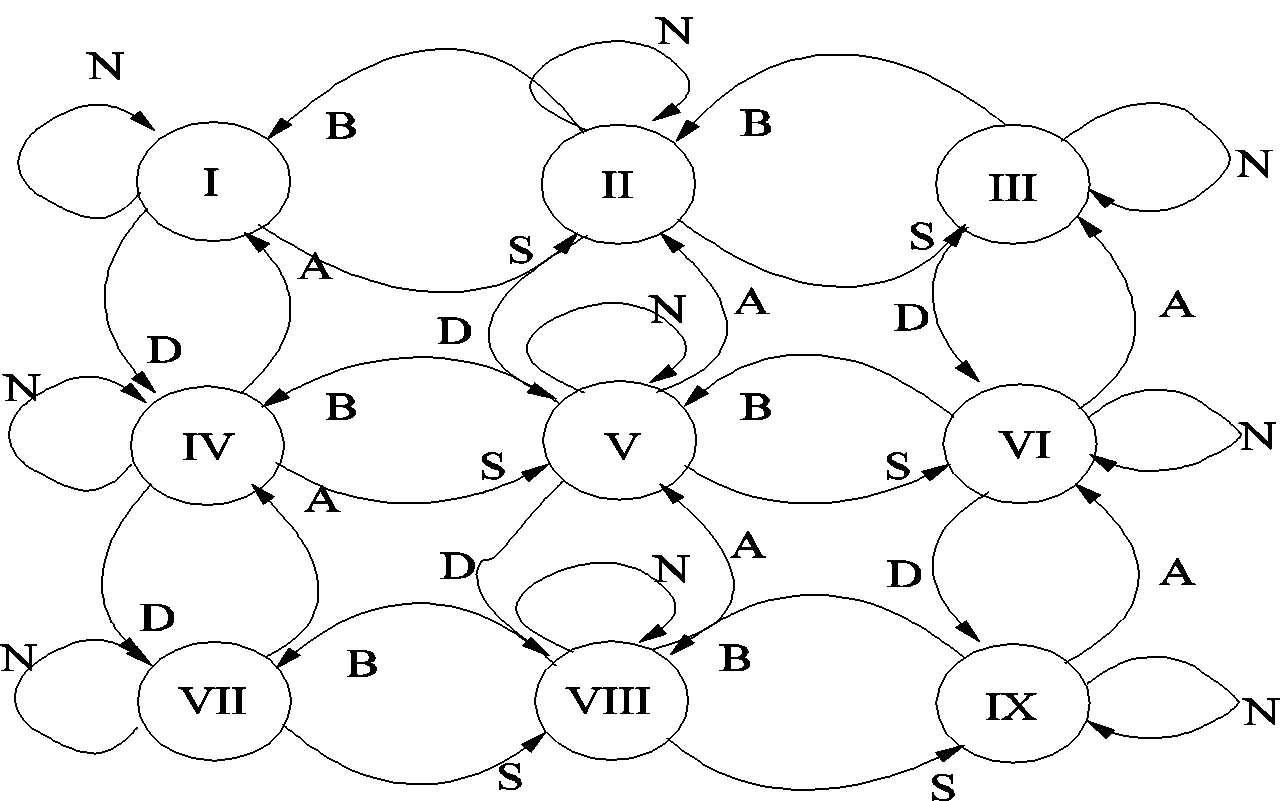
Figura 6. Autómata que describe el funcionamiento del sistema

Donde cada estado corresponde a una región de operación, y hay nueve estados. De acuerdo a los valores de las variables se deduce la ocurrencia de eventos. Las transiciones posibles son:

N: No ocurrió evento alguno.

S: Hubo un ascenso de nivel.

B: Hubo un descenso de nivel.

A: Subió la presión.

D: Disminuyó la presión disminuyó.

Un cambio de región diferente al contemplado en el autómata de la figura 6 aquí indicará un posible fallo, como se expondrá más adelante.

Determinación del estado de operación en que se encuentra el sistema de producción – función FaNC.

Para evitar cambios de estado innecesarios debido a la imprecisión de los dispositivos de medición o a efectos del oleaje dentro del depósito, se hace necesario un esquema basado en lógica difusa, que permita proyectar de forma más segura los valores numéricos resultado de los datos medidos hacia unas variables lingüísticas que representan a las regiones de operación. La figura 7 muestra el esquema de defusificación para la variable presión, proyectada a tres valores: bajo, medio y alto, con una función de membresía trapezoidal.

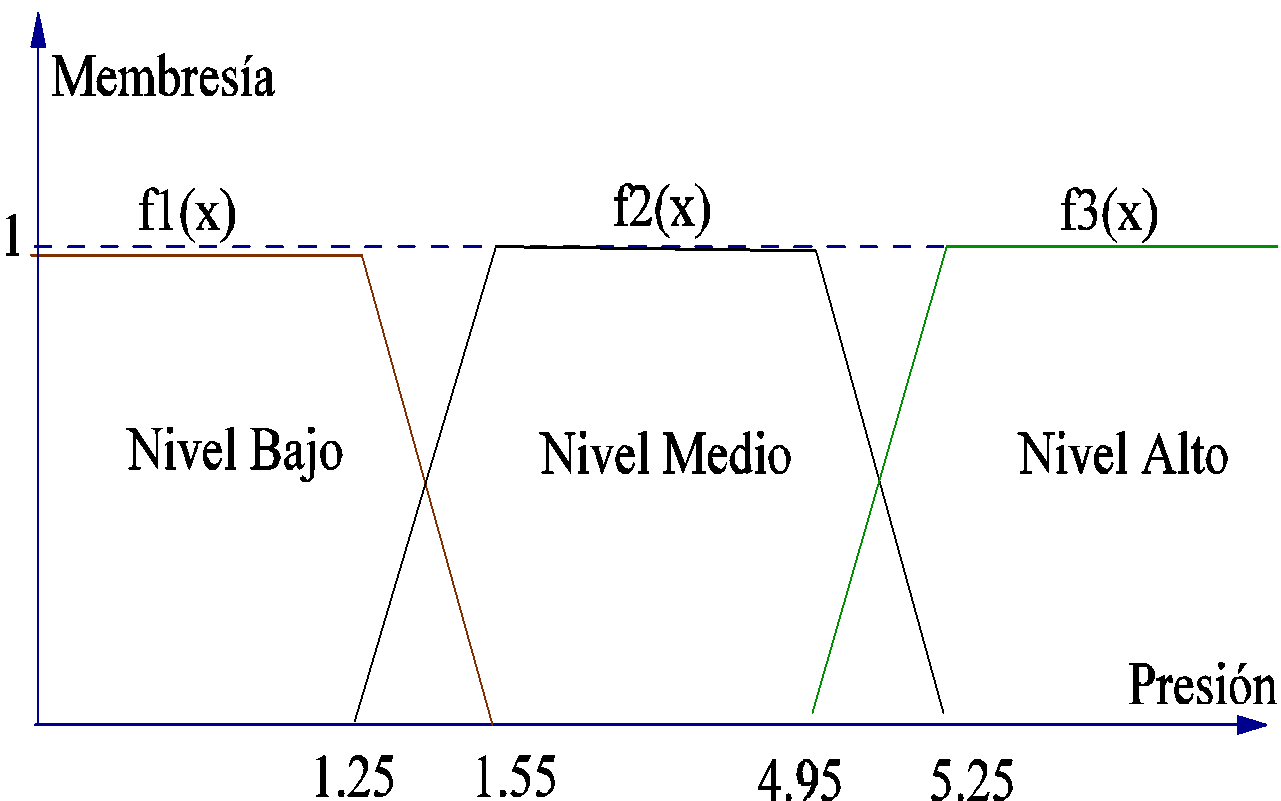
Figura 7. Funciones difusas para hallar el estado en que se encuentran la variable presión

La tabla 1 resume la clasificación para deducir en que región de operación se encuentra el sistema, dados los valores cualitativos de nivel de agua y su presión.

Tabla 1. Clasificación para hallar región de operación
Presión / Nivel	Bajo	Normal	Alto
Bajo	VII	VIII	IX
Normal	IV	V	VI
Alto	I	II	III

El cual expresado en forma de reglas quedaría de la siguiente manera, por ejemplo:

Si nivel es bajo y presión es baja, rango de operación es VII Y así sucesivamente, para las demás reglas.

Reglas para determinar la ocurrencia de eventos.

Tienen la forma:

Si región de operación es V y baja la presión, pasa a región a VIII (Ocurre evento D)

Exhaustivamente para cada región de operación se pueden definir estas reglas por medio de una tabla, como la tabla 2.

Tabla 2. Reglas para detectar eventos
Región	Cualidad de variable	Evento
I	Nivel bajo, presión alta	N
I	Nivel medio, presión alta	S
I	Nivel bajo, presión media	D
I	Otros valores	Fallo
II	Nivel medio, presión alta	N
II	Nivel medio, presión media	D
II	Nivel bajo, presión alta	B
II	Nivel bajo, presión media	D
II	Oros valores	Fallo
…	…	…
IX	Nivel alto, presión baja	N
IX	Nivel medio, presión baja	B
IX	Nivel alto, presión baja	B
IX	Nivel alto, presión media	A
Alto	Otros valores	Fallo

Fallos que se pueden presentar

Dado que este sistema se compone de dispositivos mecánicos, eléctricos y electrónicos de precisión, algunos fallos pueden presentarse, modificando su normal funcionamiento. Entre los más comunes se tienen los siguientes:

· Fallo en el compresor o existe un escape de aire (a pesar de estar encendido, la presión no aumenta, aún sin haber consumo de agua)

· Fallo en la motobomba o en el ducto del depósito externo al principal, la bomba no enciende o no hay agua en el tanque externo (está encendida, pero el nivel baja).

· Fallo en el sensor de nivel de agua o en el medidor de presión (lecturas perturbadas irregulares).

Descripción del comportamiento global del sistema – modelo cualitativo global

El estado normal de este sistema es donde operan todas las condiciones de operación que se han mencionado anteriormente. Cuando se detecta un fallo, no aplica considerar las regiones de operación de la figura 5, ya que cambiaron las condiciones del sistema. La dinámica global de este sistema sujeto a fallas se muestra en la figura 8 utilizando un autómata finito. El estado inicial es el que se etiqueta como “normal”, y ciertos eventos detectados permiten que se considere el sistema global en estado normal, mientras que otros eventos sugieren que se ha presentado un fallo. Una vez ocurre el evento F (fallo) el sistema entra al estado “Falla”, y a partir de este estado pueden ocurrir otros dos eventos: la falla es muy grave, por lo que el sistema pasa a estado “no disponible”, ocurriendo el evento E, o la falla puede repararse sin desmontar el sistema, indicando que ocurrió el evento G, que lleva al estado de reparación. Si este proceso de reparación es exitoso, el sistema entra a operación normal nuevamente, por medio del evento K. Ciertos procesos de reparación implican que el sistema se reinicie, por lo tanto, se lleva a una condición de “parada”, a partir del cual el sistema arranca (evento A) para volver a operación normal. Un ejemplo de arranque consiste en el reemplazo de una motobomba defectuosa; el depósito debe vaciarse para instalar la motobomba, y luego bombear agua y aire hasta que se coloquen en los valores de operación normal.

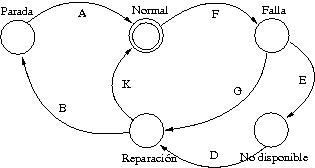
Figura 8. Autómata para modelar el comportamiento global del sistema hidroneumático

Aplicando los conceptos de teoría de lenguajes para autómata, se obtiene el lenguaje marcado del sistema. Este es:

Los eventos controlables son K, A, D y G, mientras que los eventos F, B y E son no controlables. Cuando el sistema está en modo de operación normal, opera la máquina de estados finitos de la figura 6. El único estado deseable es el de operación normal, pero dado que no se puede inhibir el evento F, el sistema puede entrar en fallo. Así mismo, el evento E no es controlable y no puede inhibirse. En razón a lo anterior, la supervisión ocurre generando eventos luego del fallo: cada vez que ocurra un evento F, entonces hacer que ocurra G y K, o si ocurre la secuencia de eventos F-E, entonces procurar generar la secuencia de eventos D-K, y así para las otras combinaciones. Puesto que el sistema hidroneumático debe operar sin detenerse, hay que considerar algunas acciones de reparación efectuadas mientras funciona el sistema.

Esquema de Razonamiento

La configuración del sistema de producción se puede establecer sobre los valores discretos de dos variables que corresponden a la motobomba y al compresor. Estos valores corresponden a On (apagado) y Off (encendido). Esta configuración varía de acuerdo a la región de operación en que se encuentra el sistema, de acuerdo al último evento detectado, y el estado en que se encuentran la motobomba y el compresor. En general, opera en forma de reglas de tipo condición–acción, de las cuales se muestra un ejemplo.

· Si variable no se ha manipulado y región es 5, entonces no manipular.

· Si la variable no se ha manipulado, y la región es otra, cambiar de acuerdo a la tabla 3.

Tabla 3. Modelo de razonamiento para la configuración del sistema hidroneumático
Z	B=Off	C=Off	B=On	C=On
1	-	-	-	C -> 0
2	-	-	-	C -> 0
3	-	-	B -> 0	C -> 0
4	-	-	-	-
5	-	-	-	-
6	-	-	-	-
7	B -> On	-	-	-
8	-	-	-	-
9	-	C -> 1	-	-

Donde “-“significa no manipular o modificar la configuración del sistema, → 0 indica que se debe apagar el dispositivo que esté encendido, y → 1 indica encender el dispositivo apagado.

Una vez se tiene este modelo racional, se derivan consignas para los controladores, según sea necesario encender o apagar tanto la bomba como el compresor, así como comandos de alto nivel para indicar que se ha producido un fallo y que se requiere una etapa de reparación o inclusive una intervención humana para reinicializar el sistema.

Validación del modelo

La naturaleza distribuida del control de procesos continuos hace que los modelos matemáticos de la física del proceso y la toma de decisiones de control se simulen de manera más apropiada usando SMA. Algunas implementaciones se han llevado a cabo diseñando una ontología de agentes para monitorear y detectar eficazmente algunos eventos relacionados con el control discreto.⁽²⁰⁾ En la figura 9 puede apreciarse el diseño de esta ontología.

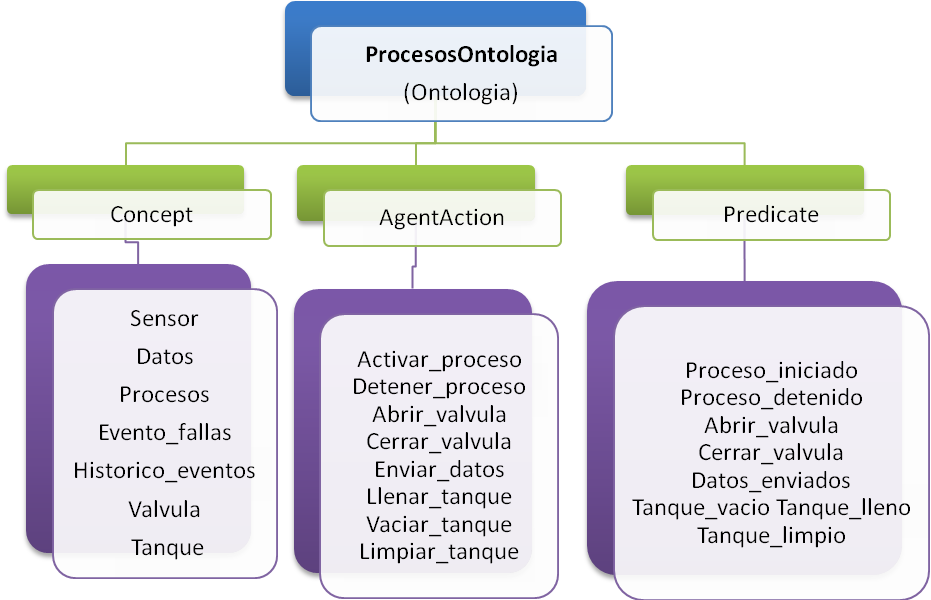
Figura 9. Ontología para la detección de eventos

Esta ontología se implementó utilizando una clase java denominada Protegé. En su validación, todos los agentes acceden a esta ontología, de manera que los mensajes son precisos en cuanto al contenido, y la semántica que debe atribuirse a dicho contenido. En la figura 10 aparece modelado en UML la secuencia de comunicación entre estos agentes.

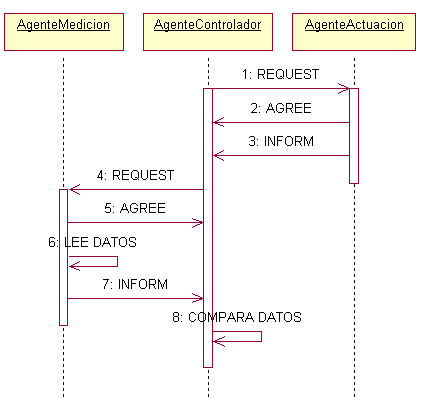
Figura 10. Secuencia de diálogo entre agentes

Para validar se utilizó un simulador basado en eventos discretos que representa a los elementos del sistema, y para ello se elaboró un programa en Java.⁽⁶⁾ En el entorno multi-agente JADE se implementaron los agentes Detector y Supervisor. Ambos agentes ejecutarán sus acciones sobre el simulador a través de una interfaz desarrollada en lenguaje Java.

Una vez implementada la plataforma de prueba con los agentes, el simulador DEVS y la interfaz, se ejecutaron las simulaciones, bajo las siguientes condiciones iniciales:

· Alturas de referencia para el nivel: 0,5 y 1,2m

· Presión de referencia: 1,47 y 5,17 Kg-f/cm2

· Flujo de entrada: 0,01 m3/seg (10 litros/seg)

· Flujo de salida variable: alrededor de 0,001 m3/seg.

· Presión inicial: 2,067 Kg-f/cm2

· Tiempo entre observaciones del agente detector de eventos: 2 segundos

RESULTADOS

Luego de ejecutar varias simulaciones, se obtuvieron trazas que representan el comportamiento de las variables del sistema bajo diversos escenarios: operación normal, fallos en un sensor y fallo en el accionamiento de la motobomba. Además de la traza de variables continuas también se muestra la traza de la evolución de los estados que representan cualitativamente el nivel y la presión, así como la evolución del estado global de la planta y las configuraciones de la planta. Una traza del nivel de agua se muestra en la figura 10, y un comportamiento similar exhibe la presión. Se puede observar primero la operación en modo normal, con los niveles del agua oscilando entre los valores máximo y mínimo, y luego se produjo un fallo en la motobomba, que hizo necesario cerrar la válvula de salida durante el tiempo de la reparación. El nivel estuvo estable durante el período de reparación debido a que no había ningún flujo de agua.

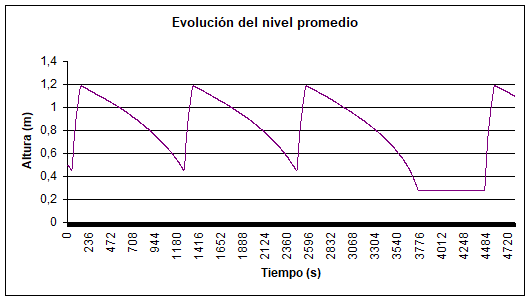
Figura 11. Evolución del nivel del agua en el depósito

También se analizó el estado del sistema mediante el registro de las trayectorias de los estados globales del sistema, al igual que las regiones cualitativas en que se encuentra el proceso en todo momento. Esto permitió hacer un seguimiento y encontrar la ocurrencia de un fallo. En la figura 11 se puede apreciar esta traza, modificando la escala de tiempo se para representar con mayor claridad los cambios de eventos ocurridos.

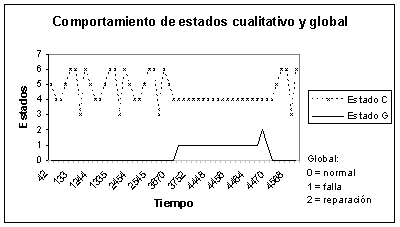
Figura 11. Traza del comportamiento de las regiones de operación y el estado del sistema

También se analizó el sistema registrando el cambio de la configuración del equipamiento en el tiempo, y confrontarla con la evolución de las variables continuas y discretas. Un fragmento de la traza de configuración tiene la siguiente forma:

Q₅ --> Q₄ --> X₁ --> Q₅ --> Q₆ --> X₂ --> Q₃ --> Q₆ --> Q₅ --> Q₄ ………

Donde Q_i indica la i-ésima región de operación, mientras que X₁ y X₂ indican las acciones de encender y apagar la motobomba, respectivamente.

CONCLUSIONES

Durante el proceso de diseño del SCS con fallos integrando diversas metodologías, su implementación y durante el proceso de modelado y simulación, se recogieron algunas experiencias, que se mencionan a continuación: se logró combinar la metodología del modelo multiresolucional con las técnicas de lógica difusa en detección de eventos, y con la teoría de control supervisorio basado en máquinas de estado finito y lenguajes formales. La simulación de eventos discretos es un método adecuado para validar el diseño de un sistema de control supervisorio, y además permite medir el desempeño del mecanismo de control de alto nivel. Con la aplicación de técnicas de lógica difusa se logra detectar eventos en variables perturbadas, que observadas de manera directa no supondrían una base sólida para indicar el estado en que se encuentra un proceso industrial. Los elementos principales de un SCS pueden implementarse por medio de agentes de software; además quedan potenciados para desempeñar labores de comunicación entre sí y con otros sistemas, bien sean automáticos o con personas.

REFERENCIAS BIBLIOGRÁFICAS

1. Lu Y, Xu X, Wang L. Smart manufacturing process and system automation – A critical review of the standards and envisioned scenarios. Journal of Manufacturing Systems. 2020;56:312–25. https://doi.org/10.1016/j.jmsy.2020.06.010

2. Dowdeswell B, Sinha R, MacDonell SG. Finding faults: A scoping study of fault diagnostics for Industrial Cyber–Physical Systems. Journal of Systems and Software. 2020;168:110638. https://doi.org/10.1016/j.jss.2020.110638

3. Bafandegan Emroozi V, Kazemi M, Doostparast M, Pooya A. Improving Industrial Maintenance Efficiency: a Holistic Approach to Integrated Production and Maintenance Planning with Human Error Optimization. Process Integration and Optimization for Sustainability. 2024;8(2):539–64. https://doi.org/10.1007/s41660-023-00374-3

4. Sanz R. Arquitectura de control inteligente de procesos [Tesis de doctorado]. Madrid: Universidad Politécnica de Madrid; 1990. http://www.aslab.org/documents/PhD/PhD-RSanz.pdf

5. Cerrada M, Aguilar J, Cardillo J, Faneite R. Agent-based design for fault management system in industrial processes. Revista Técnica de la Facultad de Ingeniería Universidad del Zulia. 2006;29:258–68. https://ve.scielo.org/scielo.php?script=sci_arttext&pid=S0254-07702006000300006

6. Guillén ML, Paredes JL, Camacho O. A proposal method for fault detection and diagnosis in chemical processes instrumentation using wavelet transform. Revista Técnica de la Facultad de Ingeniería Universidad del Zulia. 2005;28(1):68–77. https://ve.scielo.org/scielo.php?pid=S0254-07702005000100007&script=sci_abstract&tlng=en

7. Altamiranda EJ, Colina EM, Chacón ER. Intelligent supervisory systems for industrial process control. WSEAS Transactions on Systems. 2005;4(7):945–54. https://experts.illinois.edu/en/publications/intelligent-supervisory-systems-for-industrial-process-control

8. Parra Ortega C, Colina Morles E, Chacòn Ramírez E. Design framework for intelligent supervision of industrial processes. WSEAS Transactions on Systems. 2008;7(7):616–25. http://www.wseas.us/e-library/transactions/systems/2008/27-560.pdf

9. Barboza M, de Sousa Sobrinho JR, Dias J, dos Santos Filho DJ. Supervisory and Intelligent Systems. En: Bioengineering and Biomaterials in Ventricular Assist Devices. CRC Press; 2021. p. 111–32. https://www.taylorfrancis.com/chapters/edit/10.1201/9781003138358-6/supervisory-intelligent-systems-marcelo-barboza-jos%C3%A9-ricardo-de-sousa-sobrinho-jonatas-dias-diolino-jos%C3%A9-dos-santos-filho

10. Kim SH, Song KR, Kang IY, Hyon CI. On-line set-point optimization for intelligent supervisory control and improvement of Q-learning convergence. Control Engineering Practice. 2021;114:104859. https://doi.org/10.1016/j.conengprac.2021.104859

11. Jiang Y, Yin S, Li K, Luo H, Kaynak O. Industrial applications of digital twins. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2021;379(2207):20200360. https://doi.org/10.1098/rsta.2020.0360

12. Nian R, Liu J, Huang B. A review On reinforcement learning: Introduction and applications in industrial process control. Computers & Chemical Engineering. 2020;139:106886. https://doi.org/10.1016/j.compchemeng.2020.106886

13. Achouch M, Dimitrova M, Ziane K, Sattarpanah Karganroudi S, Dhouib R, Ibrahim H, et al. On Predictive Maintenance in Industry 4.0: Overview, Models, and Challenges. Applied Sciences. 2022;12(16):8081. https://doi.org/10.3390/app12168081

14. Cassandras CG, Lafortune S. Introduction to Discrete Event Systems. Boston, MA: Springer US; 2008. http://link.springer.com/10.1007/978-0-387-68612-7

15. Llano LE, Moreno J. Análisis en línea de eventos de falla en sistemas de transmisión de electricidad usando SOE, lógica difusa y sistemas expertos. Revista Técnica de la Facultad de Ingeniería Universidad del Zulia. 2013;36(2):174–82. https://ve.scielo.org/scielo.php?pid=S0254-07702013000200009&script=sci_abstract&tlng=pt

16. Malagón Sáenz E, García Mogollón AM, García Mogollón JM. Estándares de Sostenibilidad de la Gestión del Talento Humano en el Marco del Global Reporting Iniciative (GRI), Algunos Indicadores en la Institución de Educación Superior. Universidad Santo Tomás Seccional Tunja Colombia. Prospectiva (1692-8261). 2024;22(1). https://openurl.ebsco.com/EPDB%3Agcd%3A4%3A10720996/detailv2?sid=ebsco%3Aplink%3Ascholar&id=ebsco%3Agcd%3A178110907&crl=c

17. Rodríguez Fajardo LM, Donoso Anes A. Propuesta teórica de una metodología para el análisis de los riesgos empresariales por procesos y lógica difusa en el sector turístico cubano. Contaduría y Administración. 2022;67(3):348. https://doi.org/10.22201/fca.24488410e.2022.3474

18. Russell SJ, Norvig P. Artificial intelligence: a modern approach. Pearson; 2016. https://thuvienso.hoasen.edu.vn/handle/123456789/8967

19. Kowalski R. Computational logic and human thinking: how to be artificially intelligent. Cambridge University Press; 2011. https://books.google.es/books?hl=es&lr=&id=lRvWWjs8vu8C&oi=fnd&pg=PR9&ots=Nc2Vg_UziQ&sig=Lfe8g3T8LnNbgyQxp4uVeZOZAi0#v=onepage&q&f=false

20. Hernández Cruz AP, Parra Ortega CA, Portilla Granados LA. DISEÑO DE UNA ONTOLOGÍA PARA AGENTES QUE MONITOREAN MEDICIONES DE SENSORES. REVISTA COLOMBIANA DE TECNOLOGIAS DE AVANZADA (RCTA). 2017;2(26). https://doi.org/10.24054/16927257.v26.n26.2015.2385

FINANCIACIÓN

Ninguna.

CONFLICTO DE INTERESES

Los autores declaran que no existe conflicto de intereses.

CONTRIBUCIÓN DE AUTORÍA

Conceptualización: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.

Curación de datos: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.

Análisis formal: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.

Investigación: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.

Metodología: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.

Visualización: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.

Redacción – borrador original: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.

Redacción – revisión y edición: Carlos Arturo Parra Ortega, Javier Mauricio García Mogollón, Jarol Darley Ramón Valencia.