Confidence Interval for Semiparametric Regression Model Parameters Based on Truncated Spline with Application to COVID-19 Dataset in Indonesia

doi: 10.56294/dm2024.609

ORIGINAL

Confidence Interval for Semiparametric Regression Model Parameters Based on Truncated Spline with Application to COVID-19 Dataset in Indonesia

Intervalo de confianza para los parámetros del modelo de regresión semiparamétrica basado en spline truncado con aplicación al conjunto de datos COVID-19 en Indonesia

Maunah Setyawati¹ *, Nur Chamidah² *, Ardi Kurniawan² *, Dursun Aydin³ *

¹Airlangga University, Doctoral Study Program of Mathematics and Natural Sciences, Faculty of Science and Technology. Surabaya 60115, Indonesia.

²Airlangga University, Departement of Mathematics, Faculty of Science and Technology. Surabaya 60115, Indonesia.

³Muğla Sıtkı Koçman University, Department of Statistics, Faculty of Science, Muğla 48000, Turkey, and Research Scholar at Department of Mathematics, University of Wisconsin. Oshkosh Algoma Blvd, Oshkosh, WI 54901, USA.

Cite as: Setyawati M, Chamidah N, Kurniawan A, Aydin D. Confidence Interval for Semiparametric Regression Model Parameters Based on Truncated Spline with Application to COVID-19 Dataset in Indonesia. Data and Metadata. 2024; 3:.609. https://doi.org/10.56294/dm2024.609

Submitted: 18-05-2024 Revised: 17-09-2024 Accepted: 21-12-2024 Published: 22-12-2024

Editor: Adrián Alejandro Vitón Castillo

Corresponding Author: Nur Chamidah *

ABSTRACT

This study proposed a method for constructing confidence intervals for parameters in a semiparametric regression model using a truncated spline estimator, tailored for multiresponse and multipredictor longitudinal data. The semiparametric model integrated parametric and nonparametric components, facilitating the analysis of complex relationships. Confidence intervals were estimated using a pivotal quantity method.The approach was applied to COVID-19 data from Indonesia, exploring the associations between Time, Temperature, and Sunlight Intensity with the Case Increase Rate (CIR) and Case Fatality Rate (CFR). Data spanning April to November 2020 were sourced from 10 provinces with the highest CIR and CFR, obtained from http://kawalcovid.com/ and https://power.larc.nasa.gov/. The analysis identified an optimal Generalized Cross-Validation (GCV) value of 220, with one knot at 24,35°C for Temperature and two knots at 11,33 and 13 units for Sunlight Intensity. Confidence interval estimation demonstrated that all parametric components associated with Time were statistically significant, reflecting a consistent decline in CIR and CFR over time. For the nonparametric components, four parameters significantly influenced CIR, while three parameters significantly affected CFR, contingent on the knot points.The findings underscored the role of environmental factors in shaping COVID-19 dynamics and provided a robust analytical framework for future pandemic modeling. This study highlighted the utility of semiparametric regression with truncated splines in addressing complex epidemiological data, offering valuable insights for policymakers to design evidence-based mitigation strategies.

Keywords: Confidence Interval; Truncated Spline; Case Increase Rate; Case Fatality Rate; COVID-19; Temperature; Sunlight Intensity.

RESUMEN

Este estudio propuso un método para construir intervalos de confianza de los parámetros en un modelo de regresión semiparamétrica utilizando un estimador de spline truncado, diseñado para datos longitudinales con múltiples respuestas y predictores. El modelo integró componentes paramétricos y no paramétricos, facilitando el análisis de relaciones complejas. Los intervalos se estimaron mediante un método de cantidad pivotal.

El enfoque se aplicó a datos de COVID-19 en Indonesia, explorando las asociaciones entre el Tiempo, la Temperatura y la Intensidad de Luz Solar con la Tasa de Aumento de Casos (TAC) y la Tasa de Letalidad (TL). Los datos, recopilados entre abril y noviembre de 2020, provinieron de 10 provincias con las tasas más altas de TAC y TL, obtenidos de http://kawalcovid.com/ y https://power.larc.nasa.gov/. El análisis identificó un valor óptimo de Validación Cruzada Generalizada (VCG) de 220, con un nudo a 24,35°C para la Temperatura y dos nudos a 11,33 y 13 unidades para la Intensidad de Luz Solar. La estimación de intervalos de confianza mostró que todos los componentes paramétricos asociados al Tiempo fueron significativos, reflejando un descenso constante en la TAC y TL. Para los componentes no paramétricos, cuatro parámetros influyeron significativamente en la TAC y tres en la TL, dependiendo de los puntos de nudo. Los hallazgos subrayaron el papel de los factores ambientales en la dinámica del COVID-19 y ofrecieron un marco analítico robusto para futuros modelos pandémicos. Este estudio destacó la utilidad de la regresión semiparamétrica con splines truncados en el análisis de datos epidemiológicos complejos

Palabras clave: Intervalo de Confianza; Spline Truncado; Tasa de Aumento de Casos; Tasa de Letalidad Casos; COVID-19; Temperatura; Intensidad de la Luz Solar.

INTRODUCTION

In the past few years, the world has been shocked by the presence of a deadly disease. This happened because the world was unprepared to face it. In fact, its spread can be controlled if we know the nature of the disease. The disease is COVID-19 which has claimed many lives. In Indonesia, the victims reached thousands of people. Based on confirmed cases and deaths, the World Health Organization (WHO) confirmed that COVID-19 was declared a global pandemic on March 11, 2020.⁽¹⁾ The problem of a pandemic is closely related to the development rate and death rate of the pandemic disease and this can provide an overview of the severity of the disease.

Estimation of the Case Increase Rate (CIR) and Case Fatality Rate (CFR) are important elements in studying the basis of a pandemic disease.⁽²⁾ The COVID-19 infections and deaths in Europe were studied by Yuan et al.⁽³⁾ using an exponential growth model. The CIR and CFR of COVID-19 in Europe were observed and analyzed using meta-analysis.⁽⁴⁾ There are many factors that influence the development and death rates of COVID-19, including environmental factors. Analysis of the relationship between environmental factors and the spread of COVID-19 is an important study in an effort to understand how the environment can affect the spread of this virus.

Environmental factors such as temperature, humidity, sunlight intensity, wind speed, rainfall, air pollution, and crowds can have a significant impact on the transmission of COVID-19.⁽⁵⁾ Previous studies have shown that certain environmental conditions, such as lower temperatures and low sunlight intensity, tend to favor the survival of the virus in the air and on surfaces. To understand the complex relationship between environmental factors and the spread of COVID-19, a comprehensive analysis is needed. Environmental factors play a significant role in determining the extent to which COVID-19 spreads.^(6,7,8) Therefore, a research is needed to make it easier to see the pattern of the relationship between mortality rates and the spread of the disease with the factors that influence it. The knowledge obtained can later be a guideline for public policies and strategies that aim to minimize negative impacts and the final hope, the results of this study can be used as one of the materials for making policies related to mitigating future outbreaks.

In this research, there are two response variables, namely the Percentage of Case Increase Rate (CIR) and the Percentage of Case Fatality Rate (CFR) of COVID-19. Also, a parametric component of the predictor variables is Time, and a nonparametric component of the predictor variables consists of Temperature and Sunlight Intensity. Next, an analysis tool used to investigate the pattern of functional relationships between response variables and predictor variables in this study is semiparametric regression analysis.

Semiparametric regression is a combination of parametric regression and nonparametric regression. The parametric regression is used, if the form of the functional relationship between the response and predictor variables is assumed to follow a certain form. Whereas nonparametric regression will be used, if the form of the functional relationship between the response and predictor variables is assumed not to follow a certain form.⁽⁹⁾ In nonparametric regression, the estimation of the regression function is carried out based on observation data with smoothing techniques.^(10,11) These smoothing techniques are kernel,^(12,13,14) local linear,^{(15,16,17,18,19,20)} local polynomial,^(21,22) spline^{(23,24,25,26,27,28,29,30)} and mixed smoothing spline and Fourier series.⁽³¹⁾ There are several studies related to smoothing techniques for estimating regression function of the semiparametric regression model, for examples local linear,^(32,33) local polynomial,⁽³⁴⁾ spline^{(35,36,37,38,39,40,41,42)}, mixed kernel and Fourier series.⁽⁴³⁾

One important part of statistical inference is the confidence interval. In semiparametric regression, the parameters confidence interval can be used to determine the predictor variables that significantly affect the response variable. In drawing conclusions, it can be done by looking at the parameter confidence interval. If the parameter confidence interval contains a zero value, then the predictor variable does not significantly affect the response variable. Research on confidence interval of the semiparametric regression model parameters using truncated spline has been performed by Hidayati et al.⁽⁴⁴⁾. Also, researches on COVID-19 using violin plots and jitter plots techniques has been conducted by Hariyono et al.⁽⁴⁵⁾ using negative binomial regression models approaches have been discussed by Oztig et al.⁽⁴⁶⁾ and Nwosu et al.⁽⁴⁷⁾ and using Spearman-rank correlation test has been performed by Tosepu et al.⁽⁴⁸⁾.

The novelty of this research is development of theory and application in constructing confidence intervals for parameters of the multiresponse multipredictor semiparametric regression modes for both parametric and nonparametric components based on the truncated spline estimator. Therefore, this research aims to construct and estimate the confidence intervals for parameters of the multiresponse multipredictor semiparametric regression models for longitudinal data using truncated spline estimator and apply it to dataset of COVID-19 growth and mortality rates in Indonesia.

METHOD

Research Design and Data Collection

In this research we use a semiparametric regression approach with a truncated Spline estimator to analyze the relationship between Case Increase Rate (CIR), Case Fatality Rate (CFR) of COVID-19 and Time, Temperature and Sunlight Intensity in Indonesia. The CIR and CFR of COVID-19 data were obtained from the official website of the Indonesian Ministry of Health http://kawalcovid.com/, while Temperature and Sunlight Intensity data were taken from the site https://power.larc.nasa.gov/. This research data were collected from 10 provinces in Indonesia that have the highest CIR and CFR levels, namely DKI Jakarta, West Java, Central of Java, East Java, South Kalimantan, East Kalimantan, Riau, South Sulawesi, West Sumatra and North Sumatra for 8 months.

Research Variables

The response variables used in this research are Case Increase Rate (CIR) and Case Fatality Rate (CFR) of COVID-19 in Indonesia. The predictor variables used are Time, Temperature and Sunlight Intensity in Indonesia. The variables used are explained in table 1.

Table 1. Variable Structure
Notation	Variabel	Definition
Y⁽¹⁾	Case Increase Rate (CIR)	Average percentage increase in cases each month.
Y⁽²⁾	Case Fatality Rate (CFR)	Average percentage of case fatality rate per month.
X₁	Time	Number of monthly observations in a certain period.
T₁	Temperature	Average temperature per month.
T₂	Sunlight Intensity	Average Sunlight intensity per month.
Source: http://kawalcovid.com/ and https://power.larc.nasa.gov/

The semiparametric regression model is a model that is a combination of parametric and nonparametric regressions. In the semiparametric regression model, there is a nonparametric component in the form of a functional relationship that does not assume a particular function. Estimation of the regression function on the nonparametric component is done using the smoothing technique.⁽²³⁾ The smoothing technique in this research uses a spline estimator. The spline estimator was chosen because it is flexible, has good visual interpretation, and has excellent ability to handle data whose behavior changes in certain sub-intervals. One of the most commonly used types of spline estimators is the truncated spline.

Development

The semiparametric regression model where y_is^(r) represents value of r-th response for i-th subject at s-th time, is given as follows:

In Model (1), x_ips is the p-th parametric predictor, t_iqs is the q-th nonparametric predictor, b is the parametric regression coefficient, and g_q^(r)(t_iqs) is a nonparametric regression function.

The parametric components are approximated by linear functions while the nonparametric components are approximated by using truncated splines of order dq^(r) with knot points j₁, j₂, j_K_q^(r). The function of the nonparametric components can be written as follows:

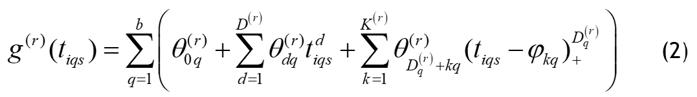
Where:

Satisfies the following equation:

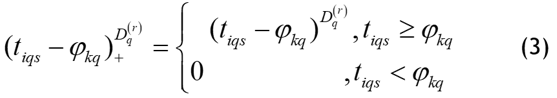
The selection of knot points in this research uses minimum value of the following GCV (Generalized Cross Validation):

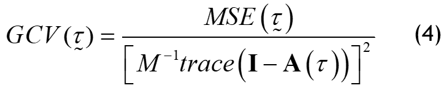
Where:

Model (1) can be expressed into matrix notation as follows:

Where:

The matrix C= [X⋮Z]

X is a matrix containing the parametric component predictors

Z is a matrix containing the nonparametric component predictors and given knot points.

While consists of parameter vectors and . Next, to determine a confidence intervals for semiparametric regression model parameters, we use Pivotal Quantity.

Statistical Analysis Steps

1. Data collection

Data was collected from April 2020 to November 2020. Temperature and Sunlight Intensity data were obtaine from the site https://power.larc.nasa.gov/. Meanwhile, CIR and CFR data were obtained from the site http://kawalcovid.com/.

2. Determining the scatter plots; correlation between response variables and patterns, and between response variables and predictor variables. The correlation between response variables must be significant. The pattern between response variables and predictors affects the approach that will be used in estimating the model. The parametric approach is used if the response variables and predictor variables follow a certain relationship pattern, while if the response variables and predictor variables do not follow a certain relationship pattern, then the nonparametric approach is used.

3. Determining the knot point based on the minimum GCV value.

4. Determining the results of the point estimation analysis in the multiresponse multipredictor semiparametric regression model based on the truncated spline estimator.

5. Determining the confidence interval for parameters of semiparametric regression model.

RESULTS

In the beginning, the pattern of relationships and correlations between variables will be discussed. In the multiresponse multipredictor semiparametric regression, information about the correlation between variables is very important. The correlation between response variables must be significant and in this study, the correlation test used is the Pearson correlation test, and the results are as follows.

Relationship Patterns and Correlations Between Response Variables

Table 2. Correlation Between CIR and CFR
Variable	Correlation Coefficient	p-value	α
CIR dan CFR	0,747	0,000	0,05

Based on table 2, we obtain that the p-value = 0,000 is less than α = 0,05, which means reject the null hypothesis, so it can be concluded that CIR and CFR of COVID-19 in Indonesia have a significant correlation. The correlation coefficient value of 0,747 indicates that there is a positive correlation between CIR and CFR.

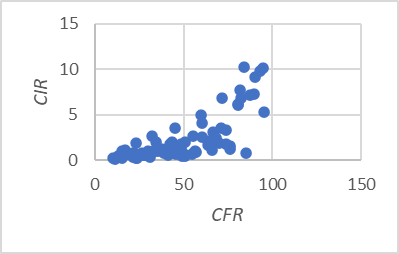
Figure 1. Scatterplot of the Relationship Pattern of CIR and CFR COVID-19

The relationship pattern shown by figure 1 indicatess a linear relationship pattern between the CIR and CFR variables.

Relationship Pattern Between Response Variables and Predictor Variables

In the multiresponse multipredictor semiparametric regression, the relationship pattern between response variables and predictor variables must be clearly known, because it will affect estimation results of the model. The relationship pattern between response variable CIR and response variable CFR with the predictor variable Time is presented in figure 2.

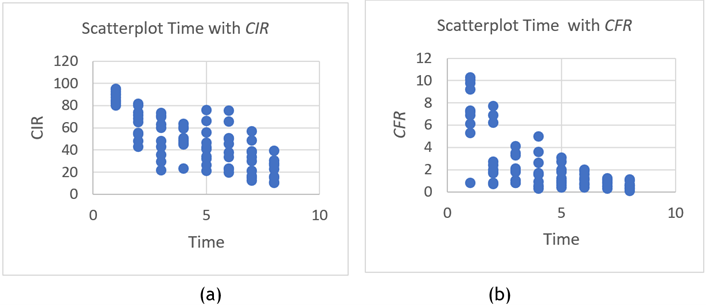
Figure 2. Scatterplots of the Relationship Pattern between Time and CIR (a), and Between Time and CFR (b)

Figure 2(a) and 2(b) show a certain relationship pattern between the predictor variable Time with the response variable CIR, and the predictor variable Time with the response variable CFR, so that the parametric approach can be used. Next, the relationship pattern between the predictor variable Temperature with the response variable CIR, and the predictor variable Temperature with the response variable CFR can be seen as in figure 3.

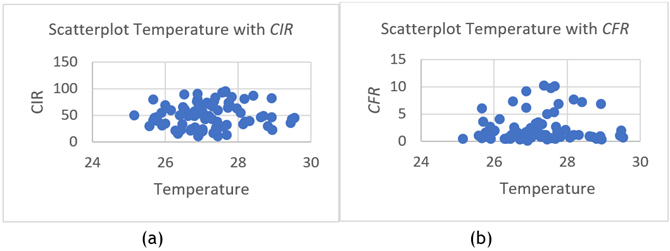
Figure 3. Scatterplots of the Relationship Pattern Between Temperature and CIR (a) and Between Temperature and CFR (b)

From figures 3(a) and 3(b), it shows that the relationship pattern between the predictor variable Temperature and the response variable CIR does not form a certain pattern, so the nonparametric approach is more appropriate to use. Likewise, the relationship pattern between the predictor variable Temperature and the response variable CFR also does not appear to form a certain pattern, so the nonparametric approach is also more appropriate to use.

The relationship pattern between the predictor variable of Sunlight Intensity and the response variable CIR and the relationship pattern between the predictor variable of Sunlight Intensity and the response variable CFR can be seen in figure 4.

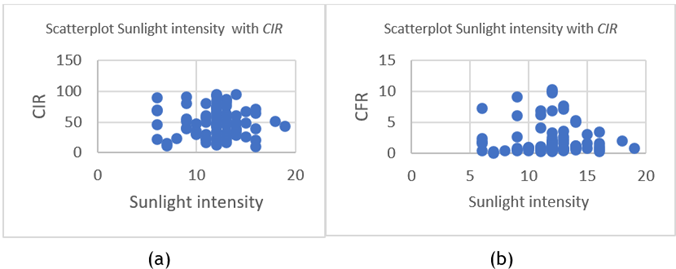
Figure 4. Scatterplots of the Relationship Pattern Between Sunlight Intensity and CIR (a) and Between Sunlight Intensity and CFR (b)

From figures 4(a) and 4(b), it shows that the pattern of the relationship between the predictor variable of sunlight intensity and the response variable CIR does not form a certain pattern, so a nonparametric approach is more appropriate to use. Likewise, the pattern of the relationship between the predictor variable of sunlight intensity and the response variable CFR also does not appear to form a certain pattern, so a nonparametric approach is also more appropriate to use.

Based on the figures 2(a) and (2b), figures 3(a) and 3(b), and figures 4(a) and 4(b), the results of predictor variables identification related to variables influencing response variables CIR and CFR of COVID-19 in Indonesia are given in table 3.

Table 3. Identification of Predictor Variables
Variable	Variable Name	Identification Results
X	Time	Parametric
T₁	Temperature	Nonparametric
T₂	Sunlight Intensity	Nonparametric

Determining Knot Points Based on Minimum GCV Values

Based on the analysis conducted, knot points and the minimum GCV values for several combinations are presented in table 4.

Table 4. Identification of Optimum Knot Points Through Minimum GCV
T₁	T₂	GCV
1 knot po0int (24,36)	1 knot point (12)	233,96
	2 knot point (11,33;13)	220,02
	3 knot point (11,12;13)	237,92
	4 knot point (11;12;12;14)	248,66
2 knot point (23,58; 25,47)	1 knot point (12)	331,99
	2 knot point (11,33; 13)	355,09
	3 knot point (11;12;13)	410,67
	4 knot point (11;12;12;14)	463,29
3 knot point(22,98; 24,36; 26)	1 knot point (12)	479,49
	2 knot point (11,33; 13)	533,36
	3 knot point (11;12;13)	623,69
	4 knot point (11;12;12;14)	704,12
4 knot point (22,67; 23,74; 25,23; 26,26)	1 knot point (12)	787,09
	2 knot point (11,33; 13)	867,76
	3 knot point (11;12;13)	977,02
	4 knot point (11;12;12;14)	1049,77

From table 4, the minimum GCV value is 220 so that the optimum knot point for the Temperature predictor T₁is at a value of 24,36, while for the Sunlight Intensity predictor T₂ it is at a value of 11,33 and 13.

The results of the point estimation analysis on the multiresponse multipredictor semiparametric regression model based on truncated spline estimator are given in table 5.

Table 5. Point Estimates of CIR and CFR Variable Parameters
Variable	Parameter	Estimator
B₀⁽¹⁾	b₀⁽¹⁾	-32,640
x₁⁽¹⁾	b₁⁽¹⁾	-8,292
B₁⁽¹⁾	q₁⁽¹⁾	0,770
t₁⁽¹⁾	q₂⁽¹⁾	4,474
(t₂-j₁₁)₊	q₃⁽¹⁾	-8,343
t₂⁽¹⁾	q₄⁽¹⁾	1,527
(t₂-j₂₁)₊	q₅⁽¹⁾	-2,083
(t₂-j₂₂)₊	q₆⁽¹⁾	-0,388
B₀⁽²⁾	b₀⁽²⁾	-2,451
x₁⁽²⁾	b₁⁽²⁾	0,058
B₁⁽²⁾	q₁⁽²⁾	-0,787
t₁⁽²⁾	q₂⁽²⁾	0,725
(t₁⁽²⁾-j₁₁)₊	q₃⁽²⁾	-0,931
t₂⁽²⁾	q₄⁽²⁾	0,074
(t₂⁽²⁾-j₂₁)₊	q₅⁽²⁾	0,002
(t₂⁽²⁾-j₂₂)₊	q₆⁽²⁾	-0,455

Based on the results of the point estimation analysis for the parameters, the data obtained are as in table 5 and then the semiparametric multi-response regression model of the truncated spline model on the 1st response (CIR) and 2nd response (CFR) are shown as follows:

For the first response, we obtain

Where:

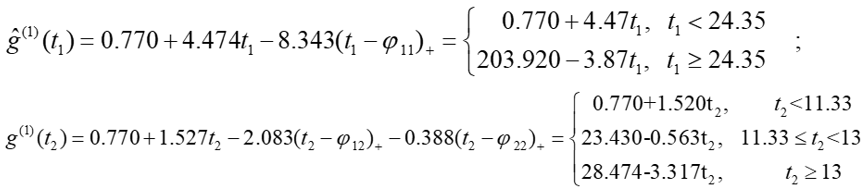
This shows that if the Temperature and Sunlight intensity are constant, then the CIR will tend to decrease by 8,292 from month to month during April to November. If the Time and Sunlight intensity variables are constant, then it is found that when the Temperature is less than 24,35⁰C, every 1⁰C increase in Temperature, the CIR of COVID-19 will increase by 4,47 cases and when the Temperature is more than 24,35⁰C, then every 1⁰C increase in Temperature will decrease the CIR of COVID-19 by 3,87 cases. If Time and Temperature are constant, then it is obtained when the Sunlight intensity is less than 11,33 units, then for every one unit increase in Sunlight Intensity, the CIR of COVID-19 will increase by 1,527 cases and when the Sunlight Intensity is between 11,33 and 13 units, then for every one unit increase in Sunlight Intensity will decrease the CIR of COVID-19 by 0,563 cases and when the Sunlight Intensity is more than 13 units, then for every one unit increase in Sunlight Intensity will decrease the CIR of COVID-19 by 3,317 cases.

For the second response, we obtain

Where:

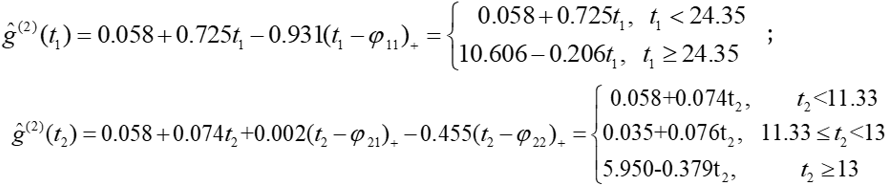
This shows that if the Temperature and Sunlight intensity are constant, the CFR of COVID-19 will tend to decrease by 0,787 from month to month during April to November. This result is in line with the results in the 1st response. If the Time and Sunlight Intensity are constant, it is found that when the Temperature is less than 24,35⁰C, then every 1⁰C increase in Temperature will increase the CFR of COVID-19 by 0,725 cases and when the Temperature is more than 24,35⁰C, then every 1⁰C increase in Temperature will decrease the CFR of COVID-19 by 0,206 cases. If Time and Temperature are constant, when the Sunlight Intensity is less than 11,33 units, then every one unit increase in Sunlight Intensity, the CFR of COVID-19 will increase by 0,074 cases, when the Sunlight Intensity is between 11,33 to 13 units, then every one unit increase in Sunlight Intensity will increase the CFR of COVID-19 by 0,076 cases and when the Sunlight Intensity is more than 13 units, then every one unit increase in Sunlight Intensity will decrease the CFR of COVID-19 by 0,379 cases.

Significant Confidence Intervals

From the point estimation, it cannot be determined which model parameters of the predictors significantly affect CIR and CFR of COVID-19, therefore confidence interval estimation needs to be done. Furthermore, from table 4, the lowest GCV result is 220 with one knot point on the Temperature variable and two knot points on the Sunlight Intensity variable. The results of the confidence interval of the parameters of the multiresponse multipredictor semiparametric regression model in the case of CIR and CFR of COVID-19 with one knot point of Temperature, namely 24,36⁰C and Sunlight Intensity 11,33 units and 13 units are as given in table 6.

Table 6. Confidence Intervals for Parameters of Semiparametric Regression Model
Respon	Parameter	Predictor	Confidence Intervals	Information
y⁽¹⁾	Parametric	b₀	P(-64,889＜(b)₀＜-0,392)=95 %	Significant
y⁽¹⁾		b₁	P(-8,669＜(b)₁＜-7,915)=95 %	Significant
y⁽²⁾		b₀	P(-4,872＜(b)₀＜-0,029)=95 %	Significant
y⁽²⁾		b₀₁	P(-0,916＜(b)₁＜-0,657)=95 %	Significant
y⁽¹⁾	Non- parametric	q₀	P(0,533＜(q)₀＜1,007)=95 %	Significant
		q₁	P(3,126＜(q)₁＜5,822)=95 %	Significant
		q₂	P(-10,593＜(q)₂＜-6,093)=95 %	Significant
		q₃	P(0,74＜(q)₃＜-2,315)=95 %	Significant
		q₄	P(-4,418＜(q)₄＜0,252)=95 %	Not significant
		q₅	P(2,222＜(q)₃＜1,445)=95 %	Not significant
y⁽²⁾		q₀	P(0,04＜(q)₀＜0,076)=95 %	Significant
		q₁	P(0,292＜(q)₁＜1,158)=95 %	Significant
		q₂	P(-1,629＜(q)₂＜-0,233)=95 %	Significant
		q₃	P(-0,159＜(q)₃＜0,306)=95 %	Not significant
		q₄	P(-0,866＜(q)₄＜0,869)=95 %	Not significant
		q₅	P(-1,306＜(q)₅＜0,396)=95 %	Not significant
Note: significant if the confidence interval does not pass through zero and vice versa if the confidence interval passes through zero then the confidence interval is not significant.

Based on table 6, it is obtained for parametric predictors, all predictors are significant both in the 1st response (CIR) and the 2nd response (CFR). While the nonparametric predictors are obtained in the 1st response (CIR) there are four significant ones and in the 2nd response (CFR) there are three significant ones

DISCUSSION

Analysis related to the relationship pattern between CIR, CFR of COVID-19 with Time, Temperature and Sunlight Intensity found that the monthly increase in cases (CIR) and the monthly case death rate (CFR) have a positive and significant correlation, meaning that the higher the CIR, the higher the CFR. This is in line with research.⁽⁴⁵⁾

If the Temperature and Sunlight intensity are constant, the CIR will tend to decrease from month to month during April to November, this is due to the policies that continue to be implemented by the Indonesian government to suppress the CIR of COVID-19 in various cities in Indonesia. One of the policies of the Indonesian government in suppressing the transmission of the COVID-19 virus is to limit community mobility. Since the beginning of the pandemic in 2020 until the first semester of 2021, the policy of restricting community mobility began with the term PSBB in April 2020 to PPKM Level 1 and 2 until the end of 2020. This is in line with research.^(46,47) Likewise, if the Temperature and Intensity of sunlight are constant, the CFR will tend to decrease. This is in line with the decrease in the CIR of COVID-19 and indeed in those months there were many policies of the Indonesian government to suppress the rate of death of COVID-19 cases in various cities in Indonesia.

The pattern of the relationship between the predictor variable Temperature with the response variables CIR and CFR did not form a certain pattern, likewise the predictor variable Intensity of sunlight with the response variables CIR and CFR also did not form a certain pattern, so the nonparametric approach is more appropriate to use. The results at Temperature that is more than or equal to 24,35, the average percentage of the increase in cases each month (CIR) and the average percentage of the death rate of cases each month (CFR) decreased, therefore in the rainy season anticipation of the spread must be more vigilant. Likewise, at Intensity of Sunlight that is more than or equal to 13 units, the CIR and CFR also decreased. In other words, the average percentage of monthly case increase (CIR) and the average percentage of monthly case fatality (CFR) decreased due to temperature and sunlight intensity.⁽²⁷⁾

The results of the confidence interval estimation for the model parameters on the Time parametric component were obtained on the CIR and CFR variables. All of these confidence intervals showed that all model parameter values, were in the negative interval and none passed zero, which means that all model parameter intervals for the Time parametric component were significant and had a negative effect. In other words, over time, CIR and CFR of COVID-19 tended to decrease.

The confidence interval estimation for the model parameters on the nonparametric components of Temperature and Sunlight Intensity showed that the model parameter values were in the negative and positive intervals, and some passed zero and some did not pass zero, which means that the confidence intervals of the model parameters for the nonparametric components of Temperature and Sunlight Intensity were significant and some were not significant, and this depends on the knot point.

In the further research, it is possible to develop confidence interval estimation for parameters of the multiresponse multipredictor semiparametric regression model using other estimators such as local linear, local polynomials, or a mixture of several of these estimators.

CONCLUSIONS

The estimation of the confidence interval of the model parameters on the Time parametric component is obtained in the CIR response and CFR response. All model parameter values are in the negative interval and none pass zero, which means that all model parameter intervals for the Time parametric component are significant. While the obtained nonparametric predictors are that in the 1st response (CIR) there are four significant ones and in the 2nd response (CFR) there are three significant ones. This conclusion shows that semiparametric regression with truncated spline estimator is very useful for predicting the average percentage of monthly case increase (CIR) and the average percentage of monthly case fatality (CFR) influenced by Time, Temperature and Sunlight Intensity. The results of this research can be used as a reference for future disaster mitigation if the case pattern is the same.

ACKNOWLEDGMENT

The authors would like to thank Dr. Budi Lestari, Drs., PG.Dip.Sc., M.Si., for providing useful comments, criticism and suggestions to improve the quality of this article.

BIBLIOGRAPHIC REFERENCES

1. Khan M, Adil SF, Alkhathlan HZ, Tahir MN, Saif S, et al. COVID-19: A global challenge with old history, epidemiology and progress so far. Molecules. 2021;26(1):39.

2. Wallinga J, Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am J Epidemiol. 2004;160(6):509-16.

3. Yuan J, Li M, Lv G, Lu ZK. Monitoring transmissibility and mortality of COVID-19 in Europe. Int J Infect Dis. 2020;95:311-5.

4. Karadag E. Increase in COVID-19 cases and case-fatality and case-recovery rates in Europe: A cross-temporal meta-analysis. J Med Virol. 2020;92(9):1511-7.

5. Irawan FA, Suhel H, Wibawanto AE. Identifikasi geospasial cuaca dan kelembapan terhadap penyebaran virus COVID-19 menggunakan sistem informasi geografis Provinsi Kalimantan Selatan. Jurnal Poros Teknik. 2020;12(2):99-106.

6. Freisya A. Analisis keterkaitan antara faktor lingkungan dan penyebaran COVID-19. J Dunia Ilmu. 2023;3(5).

7. Gil Panont A, Cordeiro Maluf J, Sepúlveda-Loyola W, Oliveira Bezerra L, da Rocha Rodrigues L, Álvarez-Bustos A, et al. Clinical, physical, and psychological outcomes among individuals with post COVID-19 syndrome with different functional status: a cross-sectional study. Salud, Ciencia y Tecnología. 2024; 4:802.

8. Nieto Sánchez ZC, Bravo Valero AJ. Exploring computational methods in the statistical analysis of imprecise medical data: between epistemology and ontology. Salud, Ciencia y Tecnología. 2024;4:1341.

9. Lestari B, Fatmawati, Budiantara IN. Spline estimator and its asymptotic properties in multiresponse nonparametric regression model. Songklanakarin J Sci Technol. 2020;42(3):533-48.

10. Eubank RL. Spline smoothing and nonparametric regression. New York: Marcel Dekker; 1988.

11. Chamidah N, Lestari B. Analisis regresi nonparametrik dengan perangkat lunak R. Surabaya: Airlangga University Press (AUP); 2022.

12. Lestari B, Fatmawati, Budiantara IN, Chamidah N. Estimation of regression function in multiresponse nonparametric regression model using smoothing spline and kernel estimators. J Phys Conf Ser. 2018;1097(1):012091.

13. Lestari B, Chamidah N, Saifudin T. Estimasi fungsi regresi dalam model regresi nonparametrik birespon menggunakan estimator smoothing spline dan estimator kernel. J Mat Stat Komputasi (JMSK). 2019;5(2):20-4.

14. Lestari B, Fatmawati, Budiantara IN, Chamidah N. Smoothing parameter selection method for multiresponse nonparametric regression model using smoothing spline and kernel estimators approaches. J Phys Conf Ser. 2019;1397(1):012064.

15. Chamidah N, Tjahjono E, Fadilah AR, Lestari B. Standard growth charts for weight of children in East Java using local linear estimator. J Phys Conf Ser. 2018;1097(1):012092.

16. Ana E, Chamidah N, Andriani P, Lestari B. Modeling of hypertension risk factors using local linear additive nonparametric logistic regression. J Phys Conf Ser. 2019;1397(1):012067.

17. Chamidah N, Zaman B, Muniroh L, Lestari B. Designing local standard growth charts of children in East Java province using a local linear estimator. Int J Innov Creat Change (IJICC). 2020;13(1):45-67.

18. Chamidah N, Yonani YS, Ana E, Lestari B. Identification the number of Mycobacterium tuberculosis based on sputum image using local linear estimator. Bull Electr Eng Informatics (BEEI). 2020;9(5):2109-16.

19. Tohari A, Chamidah N, Fatmawati, Lestari B. Modelling the number of HIV and AIDS cases in East Java using biresponse multipredictor negative binomial regression based on local linear estimator. Commun Math Biol Neurosci. 2021;73:1-17.

20. Chamidah N, Lestari B, Larasati TN, Muniroh L. Designing Z-score standard growth charts based on height-for-age of toddlers using local linear estimator for determining stunting. AIP Conf Proc. 2024;3083(1):030002. DOI: 10.1063/5.0225156.

21. Chamidah N, Gusti KH, Tjahjono E, Lestari B. Improving of classification accuracy of cyst and tumor using local polynomial estimator. TELKOMNIKA (Telecommun Comput Elec Control). 2019;17(3):1492-1500.

22. Chamidah N, Lestari B. Estimating of covariance matrix using multi-response local polynomial estimator for designing children growth charts: A theoretical discussion. J Phys Conf Ser. 2019;1397(1):012072.

23. Wahba G. Spline model for observational data. Philadelphia: Society for Industrial and Applied Mathematics; 1990.

24. Chamidah N, Lestari B, Saifudin T. Modeling of blood pressures based on stress score using least square spline estimator in bi-response nonparametric regression. Int J Innov Creat Change (IJICC). 2019;5(3):1200-16.

25. Fatmawati, Budiantara IN, Lestari B. Comparison of smoothing and truncated splines estimators in estimating blood pressure models. Int J Innov Creat Change (IJICC). 2019;5(3):1177-99.

26. Chamidah N, Lestari B, Massaid A, Saifudin T. Estimating mean arterial pressure affected by stress scores using spline nonparametric regression model approach. Commun Math Biol Neurosci. 2020;72:1-12.

27. Lestari B, Chamidah N, Aydin D, Yilmaz E. Reproducing kernel Hilbert space approach to multiresponse smoothing spline regression function. Symmetry. 2022;14(11):2227:1-22.

28. Chamidah N, Lestari B, Saifudin T, Rulaningtyas R, Wardhani P, Budiantara IN, Aydin D. Determining the number of malaria parasites on blood smears microscopic images using penalized spline nonparametric Poisson regression. Commun Math Biol Neurosci. 2024;60.

29. Aydin D, Yilmaz E, Chamidah N, Lestari B, Budiantara IN. Right-censored nonparametric regression with measurement error. Metrika (Int J Theor Appl Stats). 2024;87(3). DOI: 10.1007/s00184-024-00953-5.

30. Chamidah N, Lestari B, Susilo H, Alsagaff MY, Budiantara IN, Aydin D. Spline estimator in nonparametric ordinal logistic regression model for predicting heart attack risk. Symmetry. 2024;16(11):1440:1-23.

31. Chamidah N, Lestari B, Budiantara IN, Aydin D. Estimation of multiresponse multipredictor nonparametric regression model using mixed estimator. Symmetry. 2024;16(4):386:1-25.

32. Chamidah N, Rifada M. Local linear estimator in bi-response semiparametric regression model for estimating median growth charts of children. Far East J Math Sci (FJMS). 2016;99(8):1233-44.

33. Chamidah N, Zaman B, Muniroh L, Lestari B. Multiresponse semiparametric regression model approach to standard growth charts design for assessing nutritional status of East Java toddlers. Commun Math Biol Neurosci. 2023;30:1-23.

34. Utami TW, Chamidah N, Saifudin T. Platelet modeling in DHF patients using local polynomial semiparametric regression on longitudinal data. J Teori dan Aplikasi Mat (JTAM). 2024;8(1):231-43.

35. Tong T, Wu, He X. Coordinate ascent for penalized semiparametric regression on high-dimensional panel count data. J Comput Stat Data Anal. 2012;56:23-33.

36. Yang J, Yang H. A robust penalized estimation for identification in semiparametric additive models. Stat Probabil Lett. 2016;110:268-77.

37. Ramadan W, Chamidah N, Zaman B, Muniroh L, Lestari B. Standard growth chart of weight for height to determine wasting nutritional status in East Java based on semiparametric least square spline estimator. IOP Conf Ser: Mater Sci Eng. 2019;546(5):052063.

38. Chamidah N, Lestari B, Wulandari AY, Muniroh L. Z-score standard growth chart design of toddler weight using least square spline semiparametric regression. AIP Conf Proc. 2021;2329:060031.

39. Setyawati M, Chamidah N, Kurniawan A. Modelling Scholastic Aptitude Test of State Islamic Colleges in Indonesia using least square spline estimator in longitudinal semiparametric regression. J Phys Conf Ser. 2021;1764:012077.

40. Chamidah N, Lestari B, Budiantara IN, Saifudin T, Rulaningtyas R, Aryati A, Wardani P, Aydin D. Consistency and asymptotic normality of estimator for parameters in multiresponse multipredictor semiparametric regression model. Symmetry. 2022;14(2):336:1-18.

41. Lestari B, Chamidah N, Budiantara IN, Aydin D. Determining confidence interval and asymptotic distribution for parameters of multiresponse semiparametric regression model using smoothing spline estimator. J King Saud Univ Sci. 2023;35(5):102664.

42. Aydin D, Yilmaz E, Chamidah N, Lestari B. Right-censored partially linear regression model with error in variables: application with carotid endarterectomy dataset. Int J Biostatistics. 2023;20(1):1-34. DOI: 10.1515/ijb-2022-0044.

43. Ampa AT, Budiantarara IN, Zain I. Selection of optimal smoothing parameters in mixed estimator of kernel and Fourier series in semiparametric regression. J Phys Conf Ser. 2021;2123:012035.

44. Hidayati L, Chamidah N, Budiantara IN. Confidence interval of multiresponse semiparametric regression model parameters using truncated spline. Int J Acad Appl Res (IJAAR). 2020;4(1):14-8.

45. Hariyono E, Rahmadhani E, Kusumawardhani KD. Analysis of temperature and relative humidity towards the dispersion of COVID-19 in Indonesia. J Phys Conf Ser. 2021;1747(1):012030. DOI: 10.1088/1742-6596/1747/1/012030.

46. Oztig LI, Askin OE. Human mobility and coronavirus disease 2019 (COVID-19): A negative binomial regression analysis. Public Health. 2020;185:364-7.

47. Nwosu UI, Obite CP, Josiah M, Bartholomew DC, Izunobi HC. The role of human population density and the elements of weather in the spread of COVID-19 in Nigeria: A negative binomial regression model approach. Asian J Adv Res. 2022;17(3):30-40.

48. Tosepu R, Gunawan J, Effendy DV, Ahmad LOAI, Lestari H, Bahar H, Asfian P. Correlation between weather and COVID-19 pandemic in Jakarta, Indonesia. Sci Total Environ. 2020;725:138436.

FINANCING

This research was funded through the Research and Development of Scientific Program of the State Islamic University of Surabaya. The funds are intended to support the development of research by lecturers who are completing doctoral programs.

CONFLICT OF INTEREST

The authors declare that no conflict of interest is associated with this research. The research process was conducted objectively and independently, without influence from any stakeholder that could benefit personally or institutionally.

AUTHORSHIP CONTRIBUTION

Conceptualization: Maunah Setyawati, Nur Chamidah.

Data curation: Maunah Setyawati.

Formal analysis: Maunah Setyawati, Nur Chamidah, Ardi Kurniawan.

Acquisition of funds: Maunah Setyawati.

Research: Maunah Setyawati.

Methodology: Maunah Setyawati, Nur Chamidah, Dursun Aydin.

Project management: Maunah Setyawati, Nur Chamidah, Ardi Kurniawan.

Resources: Maunah Setyawati, Nur Chamidah, Ardi Kurniawan.

Software: Maunah Setyawati, Nur Chamidah, Dursun Aydin.

Supervision: Nur Chamidah, Ardi Kurniawan, Dursun Aydin.

Validation: Nur Chamidah, Ardi Kurniawan, Dursun Aydin.

Display: Maunah Setyawati.

Drafting - original draft: Maunah Setyawati.

Writing - proofreading and editing: Maunah Setyawati, Nur Chamidah, Ardi Kurniawan.