doi: 10.56294/dm2024.639

ORIGINAL

Time Series Clustering for Stock Exchange in Asean Based on Non-Hierarchical Methods

Agrupamiento de Series Temporales para la Bolsa de Valores en ASEAN Basado en Métodos no Jerárquicos

M. Fariz Fadillah Mardianto¹ *, Adnan Syawal Adilaha Sadikin¹, Grace Lucyana Koesnadi¹, Elly Pusporani¹, Goh Khang Wen²

¹Departement of Mathematics, Faculty of Science and Technology, Universitas Airlangga. Surabaya, Indonesia.

²Faculty of Data Science and Information Technology, INTI International University. Nilai, Malaysia.

Cite as: Fadillah Mardianto MF, Adilaha Sadikin AS, Koesnadi GL, Pusporani E, Khang Wen G. Time Series Clustering for Stock Exchange in Asean Based on Non-Hierarchical Methods. Data and Metadata. 2024; 3:.639. https://doi.org/10.56294/dm2024.639

Submitted: 12-06-2024  Revised: 14-09-2024                     Accepted: 30-12-2024                    Published: 31-12-2024

Editor: Adrián Alejandro Vitón Castillo

Corresponding Author: M. Fariz Fadillah Mardianto *

ABSTRACT

Introduction: this study explores the impact of global economic volatility, particularly influenced by the Russia-Ukraine and Israel-Palestine conflicts, on the ASEAN stock markets. The research aims to analyze stock price patterns and trends to support sustainable economic planning and improve market stability.

Method: the study employed non-hierarchical clustering techniques, including K-Means and K-Medoids, to analyze time series data from 18 ASEAN stocks over a 10-year period. Data preprocessing involved Min-Max normalization, and Principal Component Analysis (PCA) was utilized for dimensionality reduction. The clustering performance was evaluated using silhouette coefficients, and the Elbow Method determined the optimal number of clusters.

Results: K-Means demonstrated superior clustering performance with a silhouette coefficient of 0,63362 compared to K-Medoids (0,37133). The K-Means method identified seven distinct clusters, effectively grouping stocks with similar temporal patterns. The results revealed significant trends in price stability and volatility across different sectors.

Conclusions: the findings highlight the value of clustering techniques in understanding market dynamics and provide actionable insights for policymakers and investors. The study recommends the development of real-time market monitoring systems to mitigate price fluctuations and support sustainable economic growth in ASEAN. Future research could explore integrating machine learning models for enhanced market analysis.

Keywords: Time Series Clustering; Stock Exchange; Non-Hierarchical Clustering; K-Means; K-Medoids.

RESUMEN

Introducción: este estudio analiza el impacto de la volatilidad económica global, particularmente influenciada por los conflictos entre Rusia-Ucrania e Israel-Palestina, en los mercados bursátiles de la ASEAN. La investigación tiene como objetivo analizar los patrones y tendencias de los precios de las acciones para respaldar la planificación económica sostenible y mejorar la estabilidad del mercado.

Método: se emplearon técnicas de agrupamiento no jerárquicas, incluyendo K-Means y K-Medoids, para analizar datos de series temporales de 18 acciones de la ASEAN durante un período de 10 años. La preprocesamiento de datos incluyó la normalización Min-Max, y se utilizó el Análisis de Componentes Principales (PCA) para la reducción de dimensionalidad. El rendimiento del agrupamiento se evaluó utilizando coeficientes de silueta, y el Método del Codo determinó el número óptimo de grupos.

Resultados: K-Means demostró un rendimiento superior en el agrupamiento con un coeficiente de silueta de 0,63362 en comparación con K-Medoids (0,37133). El método K-Means identificó siete grupos distintos, agrupando de manera efectiva las acciones con patrones temporales similares. Los resultados revelaron tendencias significativas en la estabilidad y volatilidad de precios en diferentes sectores.

Conclusiones: los hallazgos resaltan el valor de las técnicas de agrupamiento para comprender la dinámica del mercado y proporcionan ideas prácticas para los responsables de políticas y los inversores. El estudio recomienda el desarrollo de sistemas de monitoreo del mercado en tiempo real para mitigar las fluctuaciones de precios y apoyar el crecimiento económico sostenible en la ASEAN. Investigaciones futuras podrían explorar la integración de modelos de aprendizaje automático para un análisis de mercado mejorado.

Palabras clave: Agrupamiento de Series Temporales; Bolsa de Valores; Agrupamiento no Jerárquico; K-Means; K-Medoids.

INTRODUCTION

Global economic volatility causes the world economy to fluctuate with each other. The global conflict that occurs makes global countries wary of the threat of economic decline.⁽¹⁾ This certainly has consequences for the capital market which occupies an important role in the wheels of the economy.⁽²⁾ From a macroeconomic perspective, stock exchange is one of the important references to maintain economic stability.⁽³⁾ The high level of existence of the capital market towards the economy of a country is accompanied by a high level of sensitivity of the capital market to information.⁽⁴⁾ As a result, information that causes the market to overreact can affect activities in the capital market and have an impact on global economic stability.⁽⁵⁾

In this era of globalization, relations between countries are getting closer, resulting in thin administrative boundaries. As a result, the economies between countries are interrelated and influential.⁽⁶⁾ The economic relationship also occurs in ASEAN (Association Southeast Asian Nation) which is a regional association of ten countries geographically located in the Southeast Asian region that aims to increase cooperation in the field of economy, social progress and cultural development of its member countries.⁽⁷⁾ ASEAN economic integration in the capital market is being carried out in response to existing economic conditions.⁽⁸⁾

A country’s economic growth is heavily influenced by the development of its financial sector.⁽⁹⁾ This growth is driven by policies aimed at enhancing economic monetization through expanded access to financial institutions.⁽¹⁰⁾ In ASEAN countries, the financial sector plays a dominant role in the capital market, with the top three companies in each country often belonging to the financial industry. Consequently, the financial sector in ASEAN holds significant growth potential but also faces various challenges and risks.⁽¹¹⁾ Therefore, strong regional cooperation is essential to address these risks effectively and safeguard the ASEAN economy.

One of the efforts that can be made by ASEAN countries to maintain economic stability is to group and predict stock exchanges based on a non-hierarchical clustering approach, using the K-Means and K-Medoids methods, and nonparametric time series, with the Support Vector Regression (SVR) method and Fourier Series estimators.⁽¹²⁾ Clustering is a method for grouping objects based on similarity characteristics.⁽¹³⁾ Meanwhile, nonparametric time series is a time series data analysis method that does not assume the existence of a parametric model to describe data patterns so that it is able to adjust the data flexibly.⁽¹⁴⁾ Both of these methods can be used to analyze the stock exchange data of ASEAN countries, which are dynamic, complex, and nonlinear.⁽¹⁵⁾

Previous Study

Referring to the research of Deswiaqsa et al.⁽¹⁶⁾ K-Means and K-Medoid are two distinct clustering algorithms that share conceptual similarities. Both methods partition data into predefined k clusters based on shared characteristics. The key difference lies in their approach to determine the cluster center. K-Means uses the average value of data points to define the cluster center, while K-Medoids selects an actual data object, referred to as the medoid, as the representative center of the cluster.⁽¹⁷⁾ This distinction makes comparing the performance of K-Means and K-Medoids a valuable endeavor, especially when considering their conceptual differences and similarities as outlined in the literature.⁽¹⁸⁾

In this study, the combination of these methods aims to identify patterns, trends, and relationships among variables influencing stock price movements. Furthermore, it seeks to provide accurate predictions of stock price behaviors, offering insights that can enhance investment strategies and policy decisions. By exploring the strengths and limitations of each algorithm. This study adds to the expanding body of research on efficient clustering techniques in the context of financial data analysis.

Overview and Research Objective

This study aims to compare the effectiveness of K-Means and K-Medoids clustering algorithms for time series data analysis, focusing on ASEAN stock markets to identify stock groupings, analyze price trends, and provide actionable insights for sustainable economic planning. The time series clustering process employs two non-hierarchical algorithms, K-Means and K-Medoids. The optimal cluster count is identified using the Elbow Method and silhouette coefficient, ensuring robust and reliable cluster formation. By identifying stock groupings across ASEAN in 2023 based on the dynamic characteristics of stocks, this study provides valuable insights into regional market behaviors. The findings offer practical implications for investors, policymakers, and regulators, aiding in investment decision-making, risk reduction, and enhancing market efficiency. Additionally, the study contributes to achieving the 8th Sustainable Development Goal by supporting sustainable economic planning and fostering economic stability in ASEAN countries.

METHOD

Study Design

This study utilizes a quantitative research approach to analyze time series data from ASEAN stock markets. The focus is on applying non-hierarchical clustering methods, specifically K-Means and K-Medoids, to identify stock groupings and price patterns. Principal Component Analysis (PCA) is employed to address the Curse of Dimensionality, enhancing the effectiveness of clustering.

Universe and Sample

The universe of this study includes all publicly traded stocks within ASEAN stock exchanges. The sample used consists of 18 representative stocks from various sectors: BCA, BRI, Bayan Resources, DBS, OCBC, UOB, Delta Electronics Thailand, AOT, PTT, Maybank, Public Bank, CIMB, Vietcombank, BIDV, Petro Vietnam, SMIC, SMPH, and BDO that selected based on their market influence and data availability. Weekly stock price data spanning from January 2014 to April 2024 was used, resulting in 539 observations for each stock.

Data Collection

The data was collected from reputable financial data sources, including Investing.com and Bloomberg, ensuring accuracy and completeness for analysis. Next, data preprocessing and clustering algorithms were implemented using Python programming language.

Statistical Processing

The data underwent normalization using Min-Max normalization to scale values between [0, 1]. Principal Component Analysis (PCA) was applied for dimensionality reduction, addressing the Curse of Dimensionality. Clustering was performed using K-Means and K-Medoids algorithms to group stocks based on their patterns. The quality of clustering was evaluated using the silhouette coefficient, while the Elbow Method was used to determine the optimal number of clusters.

Replication Details

To facilitate replication, this study provides detailed documentation of all data processing and analysis steps. The Python scripts used for preprocessing, clustering, PCA implementation, and result visualization are available upon request. Data preparation involved handling missing values, normalizing the dataset using Min-Max normalization, and structuring the data for analysis using Pandas and NumPy. Clustering algorithms, including K-Means and K-Medoids, were implemented using the Scikit-learn library, with specific parameters clearly defined. For performance evaluation, silhouette coefficients were calculated, and the Elbow Method graph was plotted using Matplotlib to ensure the robustness of the results. To guarantee reproducibility, a fixed random state was applied throughout the analysis, allowing other researchers to replicate the study under similar conditions using the provided guidelines and scripts.

Step Analysis

The detailed methodology for the analysis in this study is outlined below.

Algorithm of K-Means

At this classification stage, the K-Means algorithm is applied to cluster 18 stocks using the following steps:

1. Define the desired number of clusters that denoted as k.

2. Randomly initialize cluster centers by selecting data objects.

3. Compute the distance from each object to all cluster centers and assign each object to the nearest cluster.

4. Update cluster centers by computing the mean of all points within each cluster.

5. If no points change their cluster membership, the process concludes. Otherwise, repeat steps 3 to 5.

Algorithm of K-Medoids

The process for applying the K-Medoids algorithm is outlined as follows:

1. Randomly choose k data points as initial medoids.

2. Compute the Euclidean distance from each data point to all medoids.

3. Assign each object to the cluster represented by the closest medoid and compute the objective function as the sum of dissimilarities between objects and their assigned medoids.

4. Select non-medoids to replace current medoids randomly.

5. Calculate the Euclidean distance for each object against each non-medoids.

6. Reassign points to clusters based on proximity to the updated medoids and recalculate the objective function as the sum of minimum dissimilarities.

7. Compare the objective functions of the current medoids and the new medoids. Replace medoids if the new configuration reduces the objective function.

8. Repeat steps 4 through 7 until no changes occur in the representative medoids, indicating its convergence.

Algorithm of Dynamic Time Warping

1. Normalize the data to ensure consistent intervals and reorganize it on a weekly basis.

2. Select k initial points to act as medoids for clustering.

3. Compute the DTW distance matrix for all remaining points relative to the k chosen medoids.

4. Assign each data point to the nearest medoid based on DTW distance.

5. Update the medoid for each cluster by identifying the sample point with the absolute minimum error distance.

6. Repeat steps 3 to 5 until the medoids for all clusters remain unchanged, signaling the end of the process.

The steps of analysis methodology above structurally presented in figure 1.                    

Figure 1. Research Flowchart

Dynamic Time Warping (DTW)

The development of clustering analysis for time series data has advanced significantly. Various clustering algorithms, including hierarchical, grid-based, and boundary detection methods, are applicable to time series data.⁽¹⁹⁾ Instead of relying solely on linear distance calculations, such as Euclidean, Manhattan, or Canberra, the use of Dynamic Time Warping (DTW) also referred to as non-linear sequence alignment, offers a more robust method for comparing patterns. Within defined constraints, DTW is widely acknowledged for its effectiveness in determining the optimal alignment between two time-dependent sequences.

In this study, the K-Means clustering algorithm is adapted with DTW to cluster time series data.^{(20, 21)} The primary distinction between this DTW-based K-Means and the standard method lies in how the proximity between cluster members is assessed.

Given two sequences by 𝑌 and 𝑍 that represented time series data respectively:

Y={y₁,y₂,…,y_i,…,y_n}

Z={z₁,z₂,…,z_j,…,z_n}

The distance between points y_i and z_j is represented in an n×m distance matrix as D(i,j)=d(y_i, z_j). Using iterative calculations, the cumulative distance matrix M_DTW is expressed in formula 1.

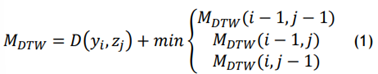
Where M_DTW is expressed represents the cumulative distance and d(yi, zj )is the minimum value among adjacent elements.

The DTW distance DTW(y,z) between sequences Y and Z is then calculated in formula 2.

Where ω_k represents the weight for the k-th path in the alignment.

Min-Max Normalization

Min-Max Normalization is a technique that applies a linear transformation to the original data, ensuring a balanced comparison between the values before and after normalization.⁽²²⁾ This process ensures consistency in scale, which is essential for clustering and other analytical techniques. This normalization adjusts the data to a specific range, typically between 0 and 1 using formula 3.

Where x’ represents the normalized value, x is the original data point, min(x) is the minimum value in the dataset, and max(x) is the maximum value in the dataset.

Principal Component Analysis

Principal Component Analysis (PCA) is a statistical technique used for multivariate analysis, primarily aimed at dimensionality reduction and detecting multicollinearity.⁽²³⁾ PCA transforms the original variables, which may be highly correlated, into new variables that are uncorrelated. This technique works effectively when applied to datasets with correlated variables. Essentially, PCA converts the original data matrix into a smaller set of homogeneous linear combinations, which retain most of the variance from the original data while achieving dimensionality reduction.⁽²⁴⁾ The process of variable reduction using PCA involves several steps as follows.

Data Standardization

The standardization process uses the Z_score method that defined by the formula 4.

Where x ̅_p is the mean for each variable which calculated using formula 5.

The standard deviation S_p is computed using formula 6.

Variance-covariance Matrix

The next step involves calculating the variance-covariance matrix which is expressed in formula 7.

The variance calculation equation is given in formula 8.

Correlation Matrix

The formula for calculating the correlation matrix is given in formula 9.

Where the correlation coefficient is expressed in formula 10.

Eigenvalues and Eigenvectors

Eigenvalue (λ) and eigenvector (v ⃗) of the correlation matrix (R_z) are determined in formula 11.

A valid eigenvalue is obtained when the determinant of the matrix equals zero that shown in formula 12.

Where I is the identity matrix corresponding to the eigenvector (v ⃗).

Principal Components (PC)

Principal Components are derived by selecting eigenvalues greater than or equal to 1, as these are considered significant. Eigenvalues below 1 are excluded. The relationship between variables and component scores is computed using formula 13.

Reduced variables are formed by creating new variables as linear combinations that expressed in formula 14.

K-Means Clustering

The purpose of K-Means Cluster Analysis is to partition existing objects into multiple clusters, where objects with similar characteristics are grouped together in the same cluster, while those with different characteristics are placed in separate clusters. The clustering process aims to minimize the objective function, which involves maximizing the variance between clusters while minimizing the variance within a cluster. The K-Means method organizes all available data into distinct groups, ensuring that each group has unique attributes compared to the others.

However, K-Means faces challenges when applied to high-dimensional data due to the phenomenon known as the “Curse of Dimensionality”.⁽²⁵⁾ In high-dimensional spaces, data points tend to be equidistant from each other and are nearly uniformly distributed. This reduces the effectiveness of the K-Means algorithm, as the distances between data points and cluster centroids may become similar across all clusters.^(26,27) Consequently, the resulting clusters may lack clarity and fail to accurately represent the underlying patterns in the data.

To address this issue, this study evaluates the performance of the K-Means clustering method in combination with Principal Component Analysis (PCA). PCA is used to reduce the dimensionality of the data, thereby mitigating the effects of the “Curse of Dimensionality” and enhancing the quality of the clustering results.

K-Medoid Clustering

Partitioning Around Medoids (PAM), commonly referred to as K-Medoids, is a clustering method that identifies representative objects, called medoids, as the center of each cluster. Other objects are then assigned to the medoid with which they share the highest resemblance. After an initial selection of 𝐾 medoids, the algorithm iteratively analyzes all possible combinations of object pairs to identify the optimal medoids. This process ensures that one object becomes a medoid while other objects are grouped as members of their respective medoids. The selection of medoids in each iteration is guided by minimizing the dissimilarities between objects and their assigned medoids.⁽²⁸⁾

The partitioning method aims to reduce the total dissimilarities between each object p and its nearest medoid by minimizing the absolute error that calculated using formula 15.

Where E represents the total absolute error for all 𝑝 objects in the data group, and denotes the medoiud of cluster C_i.⁽²⁹⁾ A notable limitation of the K-Means algorithm is its high sensitivity to outliers, which can significantly skew the clustering results. K-Medoids addresses this issue by being more robust to outliers. Outliers are data objects that deviate significantly from the general distribution of the dataset. These objects exhibit values that are substantially different, often causing distortions in clustering analysis if not appropriately managed.⁽³⁰⁾ K-Medoids effectively mitigates this sensitivity, making it a suitable alternative in datasets with outliers.

Elbow Method

The elbow method is a visual approach used to determine the optimal number of 𝑘 clusters for clustering algorithms.⁽³¹⁾ The process involves selecting a positive integer k>0, forming 𝑘 clusters in the dataset using a clustering algorithm such as K-Means, and calculating the sum of within-cluster variance, var(𝑘). A curve is then plotted between the values of 𝑘 and var(𝑘). The point at which the curve exhibits a sharp change or “elbow” indicates the appropriate number of clusters.⁽³²⁾ The within-cluster Sum of Square Error (SSE) for each cluster count is computed using the following formula.

Where Y_i  represents the value of each data point in the cluster and Y_i ̅   is the centroid of the cluster.

Silhouette Coefficient

The silhouette score is employed to evaluate the quality of clustering and identify the optimal number of clusters based on performance. Each cluster is represented by a silhouette score, which measures the density and separation of the clusters. By plotting all silhouette scores into a single diagram, the quality of the clusters can be visually compared.⁽²³⁾ The silhouette score for a given data point 𝑖 is calculated using formula 17.

Where a(i) is the average distance between the point 𝑖 and other points in the same cluster, and b(i) is the minimum average distance from point i to points in other clusters.

A silhouette score greater than zero indicates a well-defined cluster, while a score less than zero suggests that the point may be better associated with a different cluster.⁽²⁴⁾ This metric is valuable for assessing cluster cohesion and separation, aiding in the selection of optimal clusters.

RESULTS

In this study, we utilize time series data to perform clustering analysis using two distinct algorithms, both K-Means and K-Medoids. These algorithms are selected for their efficiency also widespread use in clustering tasks. The dataset comprises several time-dependent variables that need to be grouped based on their similarities and differences over time. The goal was to determine which algorithm provides better clustering performance for our stock price data.

Data Exploration

The dataset utilized in this study comprises the prices of 18 stocks: BCA, BRI, Bayan Resources, DBS, OCBC, UOB, Delta Electronics Thailand, AOT, PTT, Maybank, Public Bank, CIMB, Vietcombank, BIDV, Petro Vietnam, SMIC, SMPH, and BDO. The observation period is weekly from January 2014 to April 2024, totaling 539 weeks of observations. Figure 2 displays the time series plot for each stock.

Figure 2. Time Series Plot for Stocks Price in ASEAN

Before performing the data for time series clustering analysis, normalization is applied to adjust the values to a consistent scale within the range of [0, 1]. This step ensures that each stock has the equivalent value range, preventing any single stock with a larger scale from dominating the analysis. Normalization allows each stock to have an equal influence on the clustering process. This study utilized the min-max normalization method to scale dataset values within the range of 0 to 1, ensuring that relative proportions among the data points were maintained. This process adhered to the formula outlined in equation (3).

Optimizing K-Means Clustering with Principal Component Analysis (PCA)

This research explores the effectiveness of Principal Component Analysis (PCA) in overcoming the limitations associated with the Curse of Dimensionality when applying the K-Means clustering technique. PCA effectively reduces the dataset’s dimensions by projecting it onto a lower-dimensional space while preserving the highest possible variance. This reduction simplifies the data structure and enhances the clarity of cluster patterns.

Prior to executing the clustering algorithm, the optimal cluster count was identified using the Elbow Method. This approach assessed potential cluster counts ranging from 2 to 17, specifically designed for the dataset comprising 18 stocks. Considering practicality, forming 18 clusters was excluded. The elbow points within the assessed range are visualized in figure 3.

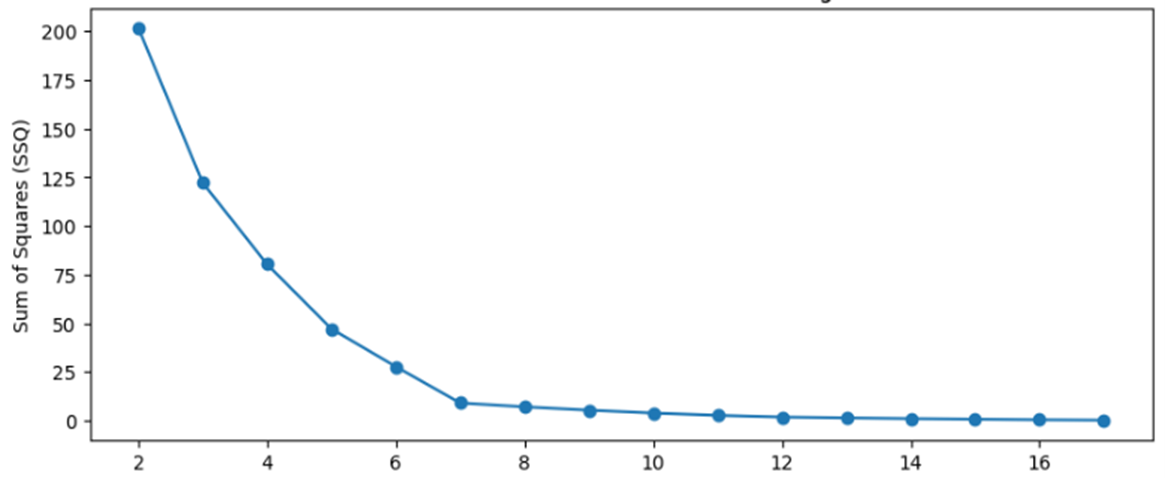
Figure 3. Elbow Method for K-Means

The optimal number of clusters, as indicated in figure 3, is identified by locating the most pronounced bend or elbow point. According to the figure, the dataset demonstrates a strong alignment with either 3 or 7 clusters. To determine the most appropriate cluster count, this study performed a comparative evaluation of data distributions for these two configurations. The results of the K-Means clustering performance for these configurations are presented in figure 4.

Figure 4. K-Means Clusters Performance; (a) 3 Clusters; (b) 7 Clusters

As depicted in figure 4, using 7 clusters provides the best fit for the dataset, allowing clear differentiation of data points based on their centroids. Therefore, the K-Means clustering technique is implemented with 7 clusters. To improve the understanding of clustering results, the time series data are represented visually according to their respective clusters, as illustrated in figure 5.

Figure 5. Time Series Cluster using K-Means Algorithm with 7 Clusters

As illustrated in figure 5, applying K-Means clustering with 7 clusters to time series data exhibits strong effectiveness in differentiating stocks based on their patterns. Stocks grouped within each cluster display comparable trends, with the red line indicating the average stock price for each cluster. The cluster distributions are further depicted in figure 6.

Figure 6. Cluster Distribution of K-Means Algorithm

The visualization of cluster distribution in figure 6 offers important insights into how stocks are grouped based on similar data patterns. This distribution serves as the basis for further analysis, with the identified clusters outlined in a table alongside their associated stock names. Table 1 provides a detailed summary of stock assignments within each cluster, connecting the visual representation of clusters to specific outcomes and corresponding stocks.

Table 1. K-Means Cluster with PCA Mapping
Cluster	Stocks
1	BIDV (VND), CIMB (MYR), SMPH (PHP), and UOB (SGD)
2	BCA (IDR) and PTT (THB)
3	DBS (SGD), BDO (PHP), and Bayan Resources (IDR)
4	BRI (IDR) and Maybank (MYR)
5	AOT (THB) and SMIC (PHP)
6	Petro Vietnam (VND)
7	Vietcombank (VND), OCBC (SGD), Public Bank (MYR), and Delta Electronics Thailand (THB)

This research utilized time series clustering to identify unique patterns in the temporal changes of stock prices. Employing the K-Means algorithm with a fixed seed to ensure reproducibility, seven distinct clusters were formed. Cluster 1 comprises the stock prices of BIDV, CIMB, SMPH, and UOB, indicating possible interlinked market activities or shared economic influences. Cluster 2 comprises BCA and PTT, reflecting similar trends possibly driven by common supply and demand dynamics. Cluster 3 shows synchronized patterns in DBS, BDO, and Bayan Resources, indicating links to shared economic conditions or market sentiments. Cluster 4 features BRI and Maybank, with comparable price dynamics potentially shaped by financial or regional market forces. Then, there are AOT and SMIC in cluster 5, pointing to shared influences within the aviation and semiconductor sectors. Cluster 6, represented by Petro Vietnam, displays a distinct pattern likely influenced by industry-specific or geopolitical factors. Lastly, Cluster 7 includes Vietcombank, OCBC, Public Bank, and Delta Electronics Thailand, highlighting possible interdependencies in the banking and electronics sectors. This clustering approach offers a systematic method for analyzing temporal patterns in stock markets, offering valuable insights into economic linkages and common influences.

Optimizing K-Medoids Clustering with Principal Component Analysis (PCA)

This research examines the use of Principal Component Analysis (PCA) to mitigate the challenges of the Curse of Dimensionality when paired with the K-Medoids clustering approach. PCA is applied for dimensionality reduction by transforming the data into a lower-dimensional space while retaining as much variance as possible. This approach simplifies the data, enhancing the clarity and interpretability of the resulting cluster patterns.

The Elbow Method was employed to identify the optimal number of clusters for the K-Medoids algorithm. This method involved evaluating cluster counts ranging from 2 to 17, tailored to the dataset comprising 18 stocks. The rationale behind this range selection was to avoid creating an excessive number of clusters that would be impractical for meaningful analysis. Figure 7 illustrates the elbow points identified for each cluster count from 2 to 17, offering insights into optimal cluster determination for subsequent analysis with the K-Medoids clustering approach.

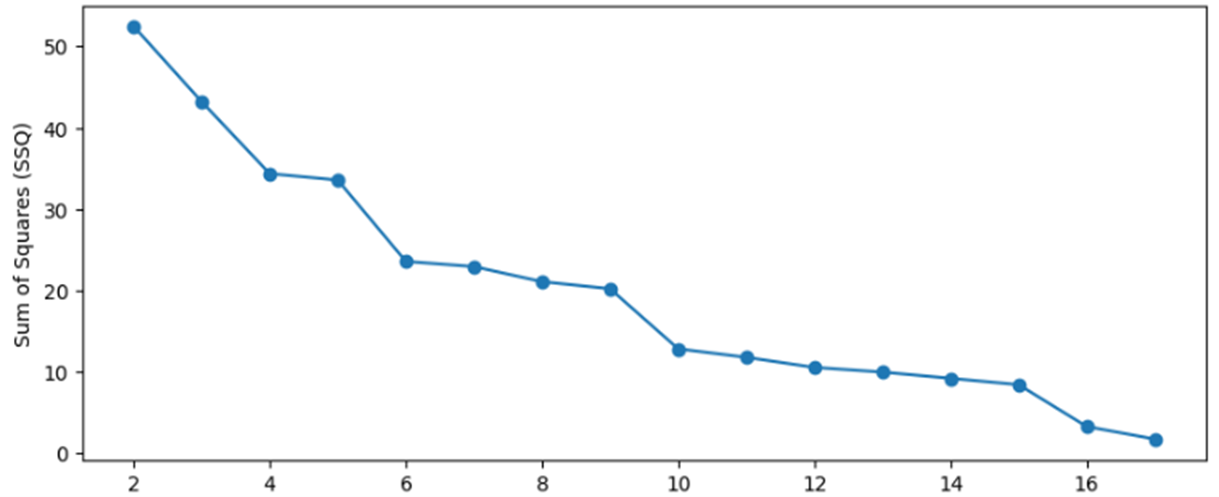
Figure 7. Elbow Method for K-Medoids

Based on figure 7, identifying the optimal number of clusters requires locating the most prominent bend or elbow in the data. Figure 7 suggests that the dataset aligns well with either 4 or 6 clusters. To establish the most suitable cluster count, this study performs a comparative analysis of data distributions for both 4 and 6 clusters. The clustering performance for these configurations using the K-Medoids method is illustrated in figure 8.

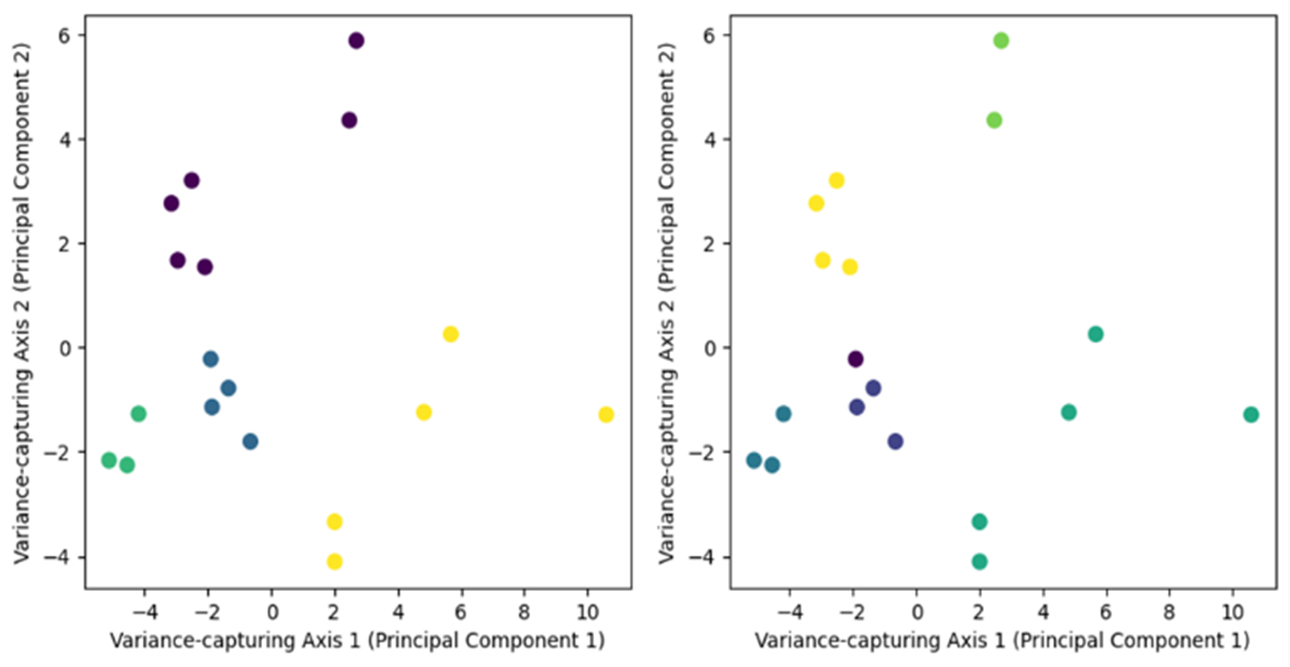
Figure 8. K-Medoids Clusters Performance; (a) 4 Clusters; (b) 6 Clusters

 As shown in figure 8, utilizing 4 clusters provides a strong fit for the data, effectively differentiating data points based on their centroids. This conclusion is further validated by the higher silhouette coefficient observed for the 4-cluster configuration. Consequently, the K-Medoids clustering analysis is conducted with 4 clusters. To enhance the interpretability of the results, the time series data is visualized according to their assigned clusters, as illustrated in figure 9.

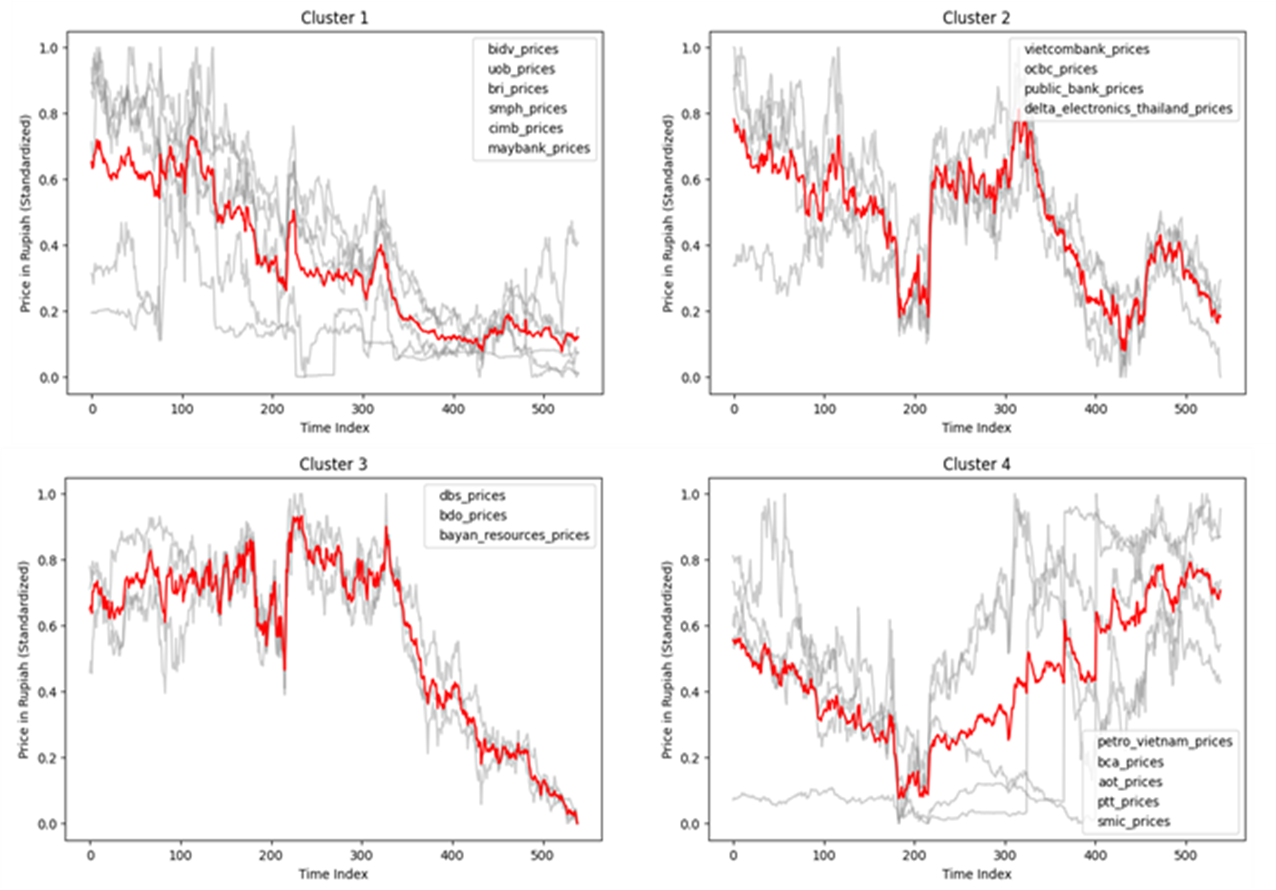
Figure 9. Time Series Cluster using K-Medoids Algorithm with 4 Clusters

Figure 9 illustrates that K-Medoids clustering with 4 clusters effectively distinguishes stocks based on their data patterns. Stocks within each cluster exhibit similar trends, with the red line representing the average price for each cluster. The detailed distribution of these clusters is further visualized in figure 10.

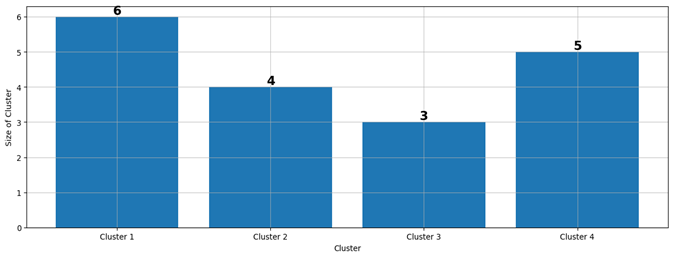
Figure 10. Cluster Distribution of K-Medoids Algorithm

The cluster distribution depicted in figure 10 offers valuable insights into how stocks are organized based on similar data patterns. This distribution lays the groundwork for further analysis, where the resulting clusters are elaborated in table 2 alongside their respective stock names. Table 2 presents a detailed summary of stock categorizations within each cluster, linking the visual representation of clusters to specific results and their corresponding stocks. This table serves as a bridge between the clustering analysis and the practical insights derived from the data.

Table 2. K-Medoids Cluster with PCA Mapping
Cluster	Stocks
1	BIDV (VND), UOB (SGD), BRI (IDR), SMPH (PHP), CIMB (MYR), and Maybank (MYR)
2	Vietcombank (VND), OCBC (SGD), Public Bank (MYR), and Delta Electronics Thailand (THB)
3	DBS (SGD), BDO (PHP), and Bayan Resources (IDR)
4	Petro Vietnam (VND), BCA (IDR), AOT (THB), PTT (THB), and SMIC (PHP)

This study applies time series clustering analysis to identify unique patterns in the temporal evolution of stock prices. Using the K-Medoids clustering algorithm with a fixed seed for consistent reproducibility, four distinct clusters were identified. Cluster 1 encompasses stock prices from BIDV, UOB, BRI, SMPH, CIMB, and Maybank, suggesting possible interconnected market dynamics or shared economic influences within financial institutions and real estate sectors. Cluster 2 includes Vietcombank, OCBC, Public Bank, and Delta Electronics Thailand, indicating similar trends potentially influenced by regional economic factors and technological markets. Cluster 3 displays synchronized patterns in DBS, BDO, and Bayan Resources stocks, possibly linked to common economic conditions or market sentiments in banking and resource sectors. Lastly, Cluster 4 comprises Petro Vietnam, BCA, AOT, PTT, and SMIC, reflecting consistent price dynamics influenced by energy, aviation, and semiconductor industries. This clustering methodology offers a structured approach to interpreting temporal patterns across diverse stock markets, highlighting potential interdependencies and shared economic influences.

DISCUSSION

The optimal clustering method between K-Means and K-Medoids is evaluated based on their performance with the previously determined optimal clusters for ASEAN stock price data. The assessment relies on the silhouette coefficient as the primary metric. This metric measures how similar an object is to its own cluster relative to other clusters. The silhouette coefficient ranges from -1 to 1, with higher values reflecting better clustering quality. Table 3 presents the silhouette coefficient values for both the K-Means and K-Medoids algorithms.

Table 3. Silhouette Coefficients for Both Methods
Algorithm	Silhouette Coefficient
KMeans with 7 Clusters	0,63362
KMedoids with 4 Clusters	0,37133

Table 3 shows that the K-Means method has the highest silhouette coefficient value compared to K-Medoids. K-Means produces better clusters in terms of density and separation than with K-Medoids. Therefore, the K-Means method was chosen as the best method for clustering time series data in this research. K-Means clustering showed several advantages over K-Medoids in this study. Firstly, K-Means had a higher silhouette coefficient, suggesting better-defined clusters. Additionally, K-Means demonstrates greater computational efficiency, particularly with large datasets, as it effectively scales with the volume of data points. This advantage is especially valuable when handling time series data with extensive observations. Additionally, K-Means is simpler to implement and interpret, making it a more practical and user-friendly option for clustering tasks in this context.

The clustering results reveal that certain stocks, grouped in Clusters 4, 5, and 7 (e.g., AOT, SMIC, BRI, Maybank), exhibit price stability driven by consistent demand, low seasonal variations, and strong market positions. Conversely, stocks in Clusters 1, 2, and 6 (e.g., BIDV, CIMB, UOB) display significant price volatility influenced by corporate performance, fiscal policies, and global market sentiment. These findings highlight the intricate dynamics of ASEAN stock markets and underscore the importance of leveraging robust analytical tools like K-Means to gain actionable insights.

The study also emphasizes the need for real-time market monitoring systems to mitigate price fluctuations and enable effective policy-making. Collaborative efforts among governments, financial institutions, and investors are essential to address stock market volatility and foster economic stability in the ASEAN region.

CONCLUSIONS

This study demonstrates that K-Means is a more effective clustering algorithm than K-Medoids for analyzing ASEAN stock price data. With a higher silhouette coefficient, K-Means provides clearer and more distinct clusters, offering valuable insights into price stability and volatility across the region. The findings contribute to a deeper understanding of ASEAN stock market dynamics and highlight the importance of using clustering techniques to support sustainable economic planning.

Policymakers and market stakeholders are encouraged to adopt real-time market monitoring systems and data-driven strategies to address price fluctuations and enhance market efficiency.

Future studies could investigate the incorporation of advanced machine learning techniques to enhance the accuracy and adaptability of clustering approaches, thereby contributing to the sustained stability and growth of ASEAN markets.

BIBLIOGRAPHIC REFERENCES

1. M. Yu, M. Umair, Y. Oskenbayev, dan Z. Karabayeva, “Exploring the nexus between monetary uncertainty and volatility in global crude oil: A contemporary approach of regime-switching,” Resources Policy, vol. 85, 2023. doi: 10.1016/j.resourpol.2023.10388.

2. H. Tan dan Z. Wang, “The impact of confucian culture on the cost of equity capital: The moderating role of marketization process,” International Review of Economics & Finance, vol. 86, pp. 112–126, 2023. doi: 10.1016/j.iref.2023.03.010.

3. C. Deng dan J. Wu, “Macroeconomic downside risk and the effect of monetary policy,” Finance Research Letters, vol. 54, 2023. doi: 10.1016/j.frl.2023.103803.

4. D. Bathia, R. Demirer, R. Ferrer, dan I. D. Raheem, “Cross-border capital flows andinformation spillovers across the equity and currency markets in emerging economies,” Journal of International Money and Finance, vol. 139, 2023. doi: 10.1016/j.jimonfin.2023.102948.

5. S. Sunardi, C. Noviolla, S. Supramono, dan Y. B. Hermanto, “Stock market reaction to government policy on determining coal selling price,” Heliyon, vol. 9, no. 2, 2023.

6. Y.-T. Tu, A. I. Aljumah, S. Van Nguyen, C.-F. Cheng, T. D. Tai, dan R. Qiu, “Achieving sustainable development goals through a sharing economy: Empirical evidence from developing economies,” Journal of Innovation & Knowledge, vol. 8, no. 1, 2023. doi: 10.1016/j .jik.2022.100299.

7. P. M. E. Killian, “ASEAN’s External Economic Relations and the Limits of Its Economic Diplomacy,” Intermestic: Journal of International Studies, vol. 6, no. 2, pp. 314-334, 2022.

8. K. Shimizu, “The ASEAN Economic Community and the RCEP in the world economy,” Journal of contemporary East Asia studies, vol. 10, no. 1, pp. 1-23, 2021. studies, 10(1), 1-23.

9. A. M. Acquah dan M. Ibrahim, “Foreign direct investment, economic growth and financial sector development in Africa,” Journal of Sustainable Finance & Investment, vol. 10, no. 4, pp. 315-334, 2020.

10. W. Dafri dan R. Al-Qaruty, “Challenges and opportunities to enhance digital financial transformation in crisis management,” Social Sciences & Humanities Open, vol. 8, no. 1, 2023. doi: 10.1016/j. ssaho.2023.100662.

11. K. Kim, “Towards sustainable and resilient ASEAN-Korea economic integration 2.0,” Asia and the Global Economy, vol. 3, no. 2, 2023. doi: 10.1016/j.aglobe.2023.100061.

12. M. F. F. Mardianto, I. S. Sediono, S. A. D. Safitri, dan N. Afifah, “Prediction of Indonesia strategic commodity prices during the COVID-19 pandemic based on a simultaneous comparison of Kernel and Fourier series estimator,” Journal of Southwest Jiaotong University, vol. 55, no. 6, 2020.

13. A. Saxena, M. Prasad, A. Gupta, N. Bharill, O. P. Patel, A. Tiwari, E. R. Joo, D. Weiping, dan C. T. Lin, “A review of clustering techniques and developments,” Neurocomputing, vol. 267, pp. 664-681, 2017.

14. E. Pusporani, M. F. F. Mardianto, A. Iffah, A. R. Firdausy, E. Widyatama, dan M. F. Huda, “Prediction of national strategic commodity prices based on multivariate nonparametric time series analysis,” Commun. Math. Biol. Neurosci., 2022.

15. Z.-M. Ren, A. Zeng, dan Y.-C. Zhang, “Structure-oriented prediction in complex networks,” Physics Reports, vol. 750, pp. 1–51, 2018. doi: 10.1016/j.physrep.2018.05.002.

16. K. Deswiaqsa, E. Darmawan, dan S. Sugiyarto, “Application of K-Means for Clustering Based on the Severity of COVID-19 in Indonesian Private Hospitals,” EKSAKTA J. Sci. Data Anal., vol. 3, no. 2, pp. 95–102, 2022. doi: 10.20885/eksakta.vol3.iss2.art5.

17. P. M. A. Putra dan I. G. A. G. A. Kadyanan, “Implementation of K-Means Clustering Algorithm in Determining Classification of the Spread of the COVID-19 Virus in Bali,” JELIKU (Jurnal Elektron. Ilmu Komput. Udayana), vol. 10, no. 1, p. 11, 2021. doi: 10.24843/jlk.2021.v10.i01.p03.

18. A. D. Andini dan T. Arifin, “Implementation of K-Medoids Algorithm for Clustering Patient Disease Data at Bandung City Hospital,” J. RESPONSIF Ris. Sains, vol. 2, no. 2, pp. 128–138, 2020.

19. E. Hernando S. O., L. Travé-Massuyès, A. Subias, M. Pavlov, dan C. Alonso, “DTW K-Means clustering for fault detection in photovoltaic modules,” XI Congreso Internacional de Ingeniería Mecánica, Mecatrónica y Automatización, 2023.

20. H. Hu, J. Liu, X. Zhang, dan M. Fang, “An Effective and Adaptable K-means Algorithm for Big Data Cluster Analysis,” Pattern Recognition, vol. 139, p. 109404, 2023.

21. A. M. Bagirov, R. M. Aliguliyev, dan N. Sultanova, “Finding compact and well-separated clusters: Clustering using silhouette coefficients,” Pattern Recognition, vol. 135, 2023.

22. T. T. Hanifa, S. Al-faraby, F. Informatika, dan U. Telkom, “Churn Prediction Analysis on PT. Telecommunications with Logistic Regression and Underbagging,” vol. 4, no. 2, pp. 3210–3225, 2017.

23. Soemartini, “Principal Component Analysis (PCA) as a Method to Solve Multicollinearity Problem,” Journal of Technology and Information, vol. 6, pp. 1-9, 2008.

24. S. Y. Ghaisani, N. Hikmah, A. H. Prasetyo, dan E. Widodo, “Hierarchical Cluster Analysis for Grouping Provinces in Indonesia Based on Indonesian Democracy Indicators in 2016,” pp. 1-11, 2018.

25. A. K. Jain, Data clustering: 50 years beyond K-Means, Pattern Recognition, 31(8), 651-666, 2010.

26. G . Wang, C. Xing, J. S. Wang, H. Y. Wang, dan J. X. Liu, “Clustering Validity Evaluation Method Based on Two Typical Clustering Algorithms,” IAENG International Journal of Computer Science, vol. 49, no. 3, 2022.

27. D. Gustian, M. Muslih, D. A. Dewi, V. Siti, R. Rustiana, dan Purnamawati, “K-Means In Clustering The Satisfaction Level of Cikundul Hot Water,” Journal of Theoretical and Applied Information Technology, vol. 101, no. 17, pp. 6980-6990, 2023.

28. M. A. Zen, S. Wahyuningsih, dan A. T. R. Dani, “Application of Time-Sequence Data Clustering with K-Medoids Algorithm,” INFERENSI, vol. 6, no. 2, pp. 117-123, 2023.

29. J. Han, M. Kamber, dan J. Pei, Data Mining: Concept and Techniques, 3rd ed., Waltham, 2012.

30. C. Holder, D. Guijo-Rubio, and A. Bagnall, “Clustering Time Series with k-Medoids Based Algorithms,” in Advanced Analytics and Learning on Temporal Data, 2023, vol. 14343, pp. 39–55, doi: 10.1007/978-3-031-49896-1_4.

31. T. M. Kodinariya and P. R. Makwana, “Review on Determining Number of Cluster in K-Means Clustering,” International Journal of Advance Research in Computer Science and Management Studies, vol. 1, no. 6, pp. 90-95, 2013. [Online]. Available: https://www.researchgate.net/publication/303117595_Review_on_Determining_of_Cluster_in_K-means_Clustering

32. J. Han, M. Kamber, and J. Pei, Data Mining: Concepts and Techniques, San Francisco, CA: Morgan Kaufmann Publishers, 2012.

FINANCING

This publication is funded by Universitas Airlangga (Unair) through Airlangga Research Fund (ARF) with the number of research contract 336/UN3.LPPM/PT.01.03/2024.

CONFLICT OF INTEREST

There is no conflict of interest.

AUTHORSHIP CONTRIBUTION

Conceptualization: M. Fariz Fadillah Mardianto, Goh Khang Wen.

Data curation: Elly Pusporani.

Formal analysis: Grace Lucyana Koesnadi.

Research: Goh Khang Wen.

Methodology: M. Fariz Fadillah Mardianto.

Project management: Elly Pusporani, Goh Khang Wen.

Resources: Adnan Syawal Adilaha Sadikin.

Software: Elly Pusporani, Adnan Syawal Adilaha Sadikin.

Supervision: M. Fariz Fadillah Mardianto.

Validation: Goh Khang Wen.

Display: Adnan Syawal Adilaha Sadikin, Grace Lucyana Koesnadi.

Drafting - original draft: Adnan Syawal Adilaha Sadikin, Grace Lucyana Koesnadi.

Writing - proofreading and editing: Grace Lucyana Koesnadi.